Bảng chia 9

I. KIẾN THỨC CẦN NHỚ

- Bảng chia ${\bf{9}}$ và phép chia trong phạm vi ${\bf{9}}$

Xuất phát từ phép nhân $9$, ta có thể nhẩm được giá trị của phép chia \(9\):

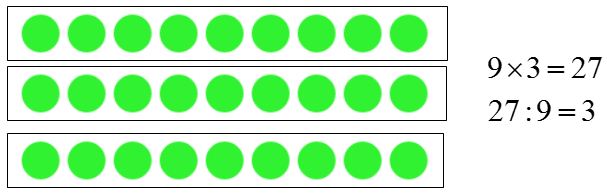
Bảng chia :

- Tìm được giá trị \(\dfrac{{\bf{1}}}{{\bf{9}}}\) của một số hoặc một hình đơn giản:

+) Chia số ban đầu cho \(9\).

+) Chia hình đã cho thành \(9\) phần bằng nhau và tô màu một phần.

II. CÁC DẠNG TOÁN

Dạng 1: Tính nhẩm

Dựa vào bảng nhân và chia \(9\) đã học, nhẩm tính các kết quả của phép nhân, chia trong phạm vi \(9\)

Ví dụ: \(54:9\)

Giải:

Nhẩm \(9 \times 6 = 54\) nên \(54:9 = 6\)

Dạng 2: Toán đố

Bước 1: Đọc và phân tích đề bài, cho giá trị của một số nhóm bằng nhau, yêu cầu tìm giá trị của “mỗi”hoặc “một” nhóm.

Bước 2: Muốn tìm giá trị của một nhóm, ta lấy giá trị của các nhóm chia cho số nhóm.

Bước 3: Trình bày lời giải.

Bước 4: Kiểm tra cách trình bày và kết quả vừa tìm được.

Ví dụ: Một bao gạo nặng \(45kg\) được chia đều vào \(9\) túi. Mỗi túi có bao nhiêu ki-lo-gam gạo ?

- Phân tích đề và tìm cách giải:

Muốn tìm khối lượng của mỗi túi thì ta lấy cân nặng của bao gạo chia đều cho \(9\)  

Giải:

Mỗi túi có số ki-lô-gam gạo là:

\(45:9 = 5\left( {kg} \right)\)

Đáp số: \(5kg\)

Dạng 3: Giá trị \(\dfrac{{\bf{1}}}{{\bf{9}}}\)

Muốn tìm $\dfrac{1}{9}$ của một số, ta cần chia số đó cho $9$.

Muốn tìm \(\dfrac{1}{9}\) của một hình thì cần chia hình đó thành \(9\) phần bằng nhau và tô một phần.

Ví dụ: Tô màu $\dfrac{1}{9}$số ô vuông dưới đây ?

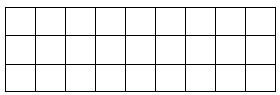
Giải:

Hình trên có \(27\) ô vuông.

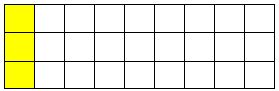
Ta có: \(27:9 = 3\)

Vậy để tô \(\dfrac{1}{9}\) số ô vuông ở hình trên thì em cần tô màu \(3\)ô vuông.

Dạng 4: Tính giá trị biểu thức

Muốn tính giá trị của biểu thức, ta cần ghi nhớ quy tắc chung:

+ Biểu thức có chứa nhân/chia và cộng trừ thì cần làm phép toán nhân/chia trước, sau đó đến các phép toán cộng/trừ.

+ Biểu thức chỉ có chứa phép nhân và phép chia thì ta thực hiện các phép toán theo thứ tự từ trái sang phải.

Ví dụ: Tính

\(\begin{array}{l}a)\,\,32:8 \times 3\\b)\,\,32 - 8:8\end{array}\)

Giải:

\(\begin{array}{l}a)\,\,32:8 \times 3 = 4 \times 3 = 12\\b)\,\,32 - 8:8 = 32 - 1 = 31\end{array}\)

Dạng 5: Tìm giá trị còn thiếu trong một phép toán

Muốn tìm số chia ta lấy số bị chia chia cho thương.

Muốn tìm số bị chia ta lấy thương nhân với số chia.

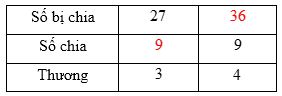
Ví dụ: Điền số còn thiếu vào bảng sau:

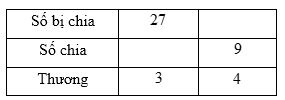
Giải:

Ta có: \(27:3 = 9\) và \(4 \times 9 = 36\) nên em điền các số vào ô trống như sau:

Dạng 6: So sánh

Bước 1: Tính giá trị các biểu thức, phép tính (Dạng 4)

Bước 2: So sánh và dùng dấu >; < hoặc = thích hợp.

Ví dụ: Phép toán có giá trị bé nhất là:

A. \(36:9\)        B. \(54:9\)          C. \(81:9\)

Giải:

Tính giá trị của các phép toán:

\(\begin{array}{l}36:9 = 4\\54:9 = 6\\81:9 = 9\end{array}\)

Vì \(9 > 6 > 4\) nên phép toán có giá trị nhỏ nhất là \(36:9\)

Dạng 7. Số dư của phép chia

- Thực hiện phép chia và tìm số dư.

- Trong phép chia, số dư bé nhất là \(1\) và số dư lớn nhất là số kém số chia một đơn vị.