Hình tam giác đều. Hình vuông. Hình lục giác đều

Lý thuyết về hình tam giác đều. hình vuông. hình lục giác đều môn toán lớp 6 sách kết nối tri thức với cuộc sống với nhiều dạng bài cùng phương pháp giải nhanh kèm bài tập vận dụng
(410) 1365 26/09/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    I. Tam giác đều

    1. Nhận biết tam giác đều

    Trong tam giác đều:

    + Ba cạnh bằng nhau

    + Ba góc bằng nhau.

    Ví dụ:

    Tam giác đều \(ABC\) có:

    + Ba cạnh bằng nhau: \(AB = BC = CA\).

    + Ba góc ở các đỉnh \(A,B,\,C\) bằng nhau.

    2. Vẽ tam giác đều

    Cách vẽ tam giác đều cạnh \(a\,(cm)\) bằng thước và compa:

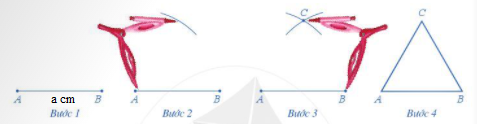
    Bước 1. Dùng thước vẽ đoạn thẳng AB = a cm

    Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB

    Bước 3. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA; gọi C là giao

    điểm của hai phần đường tròn vừa vẽ.

    Bước 4. Dùng thước vẽ các đoạn thẳng AC và BC.

    II. Hình vuông

    1.Nhận biết hình vuông

    Bốn cạnh bằng nhau: \(AB = BC = CD = DA;\)

    Hai cạnh đối \(AB\) và \(CD;\) \(AD\) và \(BC\) song song với nhau;

    Hai đường chéo bằng nhau: \(AC = BD;\)

    Bốn góc ở các đỉnh \(A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D\) là góc vuông.

    2.Vẽ hình vuông

    Ví dụ: Vẽ bằng ê ke hình vuông \(ABCD\), biết độ dài cạnh bằng \(7{\rm{ }}cm\).

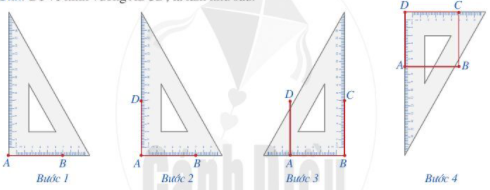
    Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB có độ dài bằng \(7{\rm{ }}cm\).

    Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD có độ dài bằng \(7{\rm{ }}cm\).

    Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC có độ dài bằng \(7{\rm{ }}cm\).

    Bước 4. Vẽ đoạn thẳng CD.

    III. Lục giác đều

    Lục giác đều \(ABCDEF\) có:

    - Sáu đỉnh A, B, C, D, E, F

    - Sáu cạnh bằng nhau: \(AB = BC = CD = DE = EF\).

    - Sáu góc ở các đỉnh A, B, C, D, E, F bằng nhau.

    - Ba đường chéo chính bằng nhau \(AD = BE = CF\).

    Chú ý:

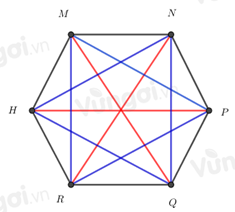
    Cho hình lục giác đều \(MNPQRH\) như hình vẽ:

    - MP, PR, MR, NQ, QH, HN được gọi là các đường chéo phụ của hình lục giác đều.

    - Độ dài các đường chéo phụ bằng nhau.

    - Các đường chéo chính cắt nhau tại 1 điểm.

    - Mỗi góc của hình lục giác đều bằng \({120^0}\).

    Xem toàn bộ nội dung Toán 6 - KNTT:

    (410) 1365 26/09/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 6 Toán 6 - KNTT