Đề thi thử THPT QG năm 2021 môn Toán - Trường THPT Nguyễn Văn Thoại lần 2
Đề thi thử THPT QG năm 2021 môn Toán - Trường THPT Nguyễn Văn Thoại lần 2
-
Hocon247
-
50 câu hỏi
-
90 phút
-
68 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Trong không gian tọa độ Oxyz, đường thẳng \(\left( d \right):\frac{x+5}{2}=\frac{y-7}{-8}=\frac{z+13}{9}\) có một véc tơ chỉ phương là
Đường thẳng \(\left( d \right):\frac{x+5}{2}=\frac{y-7}{-8}=\frac{z+13}{9}\) có véc tơ chỉ phương là \(\vec{u}=\left( 2;\,-8;\,9 \right).\)
Nên \(\overrightarrow{{{u}_{1}}}=\left( 2;\,-8;\,9 \right)\) là véc tơ chỉ phương của \(\left( d \right).\)
Hình vẽ bên là đồ thị của hàm số nào?
.jpg.png)
Đồ thị đã cho là đồ thị của hàm số bậc 4 trùng phương, nên loại đáp án A và B.
Ta có \(\underset{x\to +\infty }{\mathop{\lim }}\,y=-\infty \) suy ra a<0 nên loại C.
Trong không gian Oxyz, mặt phẳng \(\left( \alpha \right):x-y+2z-3=0\) đi qua điểm nào dưới đây?
Xét điểm \(M\left( 1\,;\,1;\,\frac{3}{2} \right)\), ta có: \(1-1+2.\frac{3}{2}-3=0\) đúng nên \(M\in \left( \alpha\right)\) nên A đúng.
Xét điểm \(N\left( 1\,;-1\,;-\frac{3}{2} \right)\), ta có: \(1+1+2.\left( -\frac{3}{2} \right)-3=0\) sai nên \(N\notin \left( \alpha\right)\) nên B sai.
Xét điểm \(P\left( 1\,;\,6\,;\,1 \right)\), ta có: 1-6+2.1-3=0 sai nên \(P\notin \left( \alpha\right)\) nên C sai.
Xét điểm \(Q\left( 0\,;\,3\,;\,0 \right)\), ta có: 0-3+2.0-3=0 sai nên \(Q\notin \left( \alpha \right)\) nên D sai.
Với \(\alpha \) là một số thực bất kỳ, mệnh đề nào sau đây sai?
+) Có \(\sqrt{{{10}^{\alpha }}}={{10}^{\frac{\alpha }{2}}}\) với mọi \(\alpha \), nên A đúng.
+) Có \({{\left( {{10}^{\alpha }} \right)}^{2}}={{\left( 100 \right)}^{\alpha }}\) với mọi \(\alpha \), nên B đúng.
+) Có \(\sqrt{{{10}^{\alpha }}}={{\left( \sqrt{10} \right)}^{\alpha }}\) với mọi \(\alpha \), nên C đúng.
+) Có \({{\left( {{10}^{\alpha }} \right)}^{2}}={{10}^{{{\alpha }^{2}}}}\) (*), dấu đẳng thức xảy ra khi \(\alpha =0\) hoặc \(\alpha =2\).
Lấy \(\alpha =1\) thì (*) sai, vậy D sai.
Tính diện tích xung quanh \(S\) của khối trụ có bán kính đáy \(r=4\) và chiều cao \(h=3.\)
\(S = 2\pi rh = 2\pi .4.3 = 24\pi \)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \(\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y-4z-25=0\). Tìm tọa độ tâm I và bán kính R của mặt cầu \(\left( S \right)\).
Ta có: \(\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y-4z-25=0\Leftrightarrow {{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}+{{\left( z-2 \right)}^{2}}=34\)
Vậy \(I\left( 1;-2;2 \right); R=\sqrt{34}\).
Trong không gian Oxyz, hình chiếu vuông góc của điểm \(A\left( 3\,;\,2\,;\,-4 \right)\) lên mặt phẳng \(\left( Oxy \right)\) có tọa độ là
Gọi \({A}'\) là hình chiếu vuông góc của điểm \(A\left( 3\,;\,2\,;\,-4 \right)\) lên mặt phẳng \(\left( Oxy \right)\), ta có \({A}'\,\left( 3\,;\,2\,;\,0 \right)\).
Cho dãy số \(\frac{1}{2};0;-\frac{1}{2};-1;-\frac{3}{2};.....\) là cấp số cộng với
Nếu dãy số \(\left( {{u}_{n}} \right)\) là một cấp số cộng thị công sai d của nó là hiệu của một cặp số hạng liên tiếp bất kì (số hạng sau trừ cho số hạng trước) của dãy số đó.
Ta có \(\frac{1}{2};0;-\frac{1}{2};-1;-\frac{3}{2};.....\) là cấp số cộng \( \Rightarrow \left\{ \begin{array}{l} {u_1} = \frac{1}{2}\\ {u_2} - {u_1} = - \frac{1}{2} = d \end{array} \right.\)
Đạo hàm của hàm số \(y={{\pi }^{x}}\) là
\(y' = {\pi ^x}.\ln \pi \)
Cho tập hợp A gồm có 9 phần tử. Số tập con gồm có 4 phần tử của tập hợp A là
Số tập con gồm có 4 phần tử của tập hợp A là \(C_{9}^{4}\).
Cho hàm số \(y=f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có bảng xét dấu \({f}'\left( x \right)\) như sau
.png)
Mệnh đề nào sau đây sai?
Dựa vào bảng xét dấu \({f}'\left( x \right)\) ta nhận thấy hàm số không đạt cực đại tại \({{x}_{0}}=-2\) vì \({f}'\left( x \right)\) không đổi dấu khi x đi qua điểm \({{x}_{0}}=-2\).
Cho đồ thị hàm số \(y=f\left( x \right)\) có đồ thị như hình vẽ bên dưới
.jpg.png)
Hàm số \(y=f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
Dựa vào đồ thị hàm số \(y=f\left( x \right)\) ta có hàm số đồng biến (đồ thị đi lên) trên khoảng (0;2).
Cho hàm \(f\left( x \right)\) có đạo hàm liên tục trên \(\left[ 2;3 \right]\) đồng thời \(f\left( 2 \right)=2,f\left( 3 \right)=5\). Khi đó \(\int\limits_{2}^{3}{{f}'\left( x \right)}\text{d}x\) bằng
\(\int\limits_2^3 {f'\left( x \right)} {\rm{d}}x = f\left( 3 \right) - f\left( 2 \right) = 5 - 2 = 3\)
Cho số phức \(z=-1+2i\,,\,w=2-i\). Điểm nào trong hình bên biểu diễn số phức z+w?
.jpg.png)
z + w = 1 + i
Do đó điểm biểu diễn của số phức z+w là \(P\left( 1\,;\,1 \right).\)
Cho khối chóp S.ABC có SA, SB, SC đôi một vuông góc và SA=a, SB=b, SC=c. Tính thể tích V của khối chóp đó theo a, b, c.
Áp dụng công thức thể tích khối tứ diện vuông \(V = \frac{{SA.SB.SC}}{6} = \frac{{abc}}{6}\)
Cho số phức \({{z}_{1}}=1+i\) và \({{z}_{2}}=2-3i\). Tìm số phức liên hợp của số phức \(\text{w}={{z}_{1}}+{{z}_{2}}\)?
\({\rm{w}} = {z_1} + {z_2} = 1 + i + 2 - 3i \Rightarrow {\rm{w}} = 3 - 2i \Rightarrow \overline {\rm{w}} = 3 + 2i\)
Cho hàm số \(f\left( x \right)={{2}^{x}}+x+1\). Tìm \(\int{f\left( x \right)\text{d}x}\)
\(\int {\left( {{2^x} + x + 1} \right){\rm{d}}x} = \frac{1}{{\ln 2}}{2^x} + \frac{1}{2}{x^2} + x + C\)
Đường tiệm cận ngang, đường tiệm cận đứng của đồ thị hàm số \(y=\frac{2x-1}{x-2}\) lần lượt có phương trình là
Ta có:
\(\underset{x\to +\infty }{\mathop{\lim }}\,\frac{2x-1}{x-2}=2;\,\,\underset{x\to -\infty }{\mathop{\lim }}\,\frac{2x-1}{x-2}=2\), suy ra đường thẳng y=2 là phương trình đường tiệm cận ngang.
\(\underset{x\to {{2}^{+}}}{\mathop{\lim }}\,\frac{2x-1}{x-2}=+\infty ;\,\,\underset{x\to {{2}^{-}}}{\mathop{\lim }}\,\frac{2x-1}{x-2}=-\infty \), suy ra đường thẳng x=2 là phương trình đường tiệm cận đứng.
Đường tiệm cận ngang, đường tiệm cận đứng của đồ thị hàm số lần lượt là y=2,x=2
Nghiệm của bất phương trình \({{3}^{x+2}}\ge \frac{1}{9}\) là
\({3^{x + 2}} \ge \frac{1}{9} \Leftrightarrow {3^{x + 2}} \ge {3^{ - 2}} \Leftrightarrow x + 2 \ge - 2 \Leftrightarrow x \ge - 4\)
Cho hình nón có bán kính đáy \(r=\sqrt{3}\) và độ dài đường sinh l=4. Tính diện tích xung quanh \({{S}_{xq}}\) của hình nón đã cho.
Ta có diện tích xung quanh của hình nón là \({{S}_{xq}}=\pi rl\), với \(r=\sqrt{3}, l=4\).
Suy ra \({{S}_{xq}}=4\sqrt{3}\pi \)
Vậy hình nón có bán kính đáy \(r=\sqrt{3}\) và độ dài đường sinh l=4 có diện tích xung quanh là \({{S}_{xq}}=4\sqrt{3}\pi \).
Cho tứ diện ABCD có AC=AD và BC=BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?
.png)
Nếu AB không vuông góc với \(\left( BCD \right)\) nên góc giữa 2 mặt phẳng \(\left( ABC \right)\) và \(\left( ABD \right)\) không thể là góc \(\widehat{CBD}\).
Xét đáp án B có:
\(\left. \begin{array}{l} CD \bot AI\\ CD \bot BI \end{array} \right\} \Rightarrow CD \bot \left( {AIB} \right)\) ; \(CD\subset \left( BCD \right)\) nên \(\left( BCD \right)\bot \left( AIB \right)\). B đúng.
Chứng minh tương tự \(\left( ACD \right)\bot \left( AIB \right)\). D đúng.
Xét đáp án A:
\(\left. \begin{array}{l} CD \bot AI\\ CD \bot BI\\ CD = \left( {ACD} \right) \cap \left( {BCD} \right) \end{array} \right\} \Rightarrow \) Góc giữa 2 mặt phẳng \(\left( ACD \right)\) và \(\left( BCD \right)\) là góc giữa \(\widehat{\left( AI;BI \right)}\) .
Biết rằng có duy nhất một cặp số thực \(\left( x;\ y \right)\) thỏa mãn \(\left( x+y \right)+\left( x-y \right)i=5+3i\). Tính S=x+2y.
\(\left( {x + y} \right) + \left( {x - y} \right)i = 5 + 3i \Leftrightarrow \left\{ \begin{array}{l} x + y = 5\\ x - y = 3 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = 4\\ y = 1 \end{array} \right. \Rightarrow S = 6\)
Giá trị lớn nhất của hàm số \(f\left( x \right)=\frac{{{x}^{2}}-8x}{x+1}\) trên đoạn \(\left[ 1;3 \right]\) bằng
Tập xác định: \(D=\mathbb{R}\backslash \left\{ -1 \right\}\).
Đạo hàm: \({f}'\left( x \right)=\frac{{{x}^{2}}+2x-8}{{{\left( x+1 \right)}^{2}}}\).
Xét \({f}'\left( x \right)=0\Leftrightarrow {{x}^{2}}+2x-8=0\Leftrightarrow \left[ \begin{align} & x=2\in \left[ 1\,;\,3 \right] \\ & x=-4\notin \left[ 1\,;\,3 \right] \\ \end{align} \right.\)
Ta thấy hàm số đã cho liên tục và có đạo hàm trên đoạn \(\left[ 1\,;\,3 \right]\).
Ta có: \(f\left( 1 \right)=-\frac{7}{2}; f\left( 3 \right)=-\frac{15}{4}; f\left( 2 \right)=-4\).
Vậy \(\underset{\left[ 1\,;\,3 \right]}{\mathop{\max }}\,f\left( x \right)=f\left( 1 \right)=-\frac{7}{2}\).
Số nghiệm của phương trình \({{\log }_{2}}\left( {{x}^{2}}\,-\,\,x\,+\,2 \right)=1\) là
Theo giả thiết ta có:
\({\log _2}\left( {{x^2}\, - \,\,x\, + \,2} \right) = 1\, \Leftrightarrow \,{x^2}\, - \,\,x\, + \,2\, = \,{2^1} \Leftrightarrow \,{x^2}\, - \,\,x\, + \,2\, - \,2\, = \,0\)
\( \Leftrightarrow \,{x^2}\, - \,\,x\,\, = \,0 \Leftrightarrow \,\left[ \begin{array}{l} x\,\, = \,0\\ x\,\, = \,1 \end{array} \right.\)
Vậy phương trình đã cho có hai nghiệm phân biệt
Nguyên hàm của hàm số \(f\left( x \right)=\sqrt{3x+2}\) là
+ Đặt: \(t=\sqrt{3x+2}\to {{t}^{2}}=3x+2\to \frac{2t\text{dt}}{3}=\text{d}x\).
+ Khi đó: \(\int{\left( \sqrt{3x+2} \right)}\text{d}x=\int{t.}\frac{\text{2tdt}}{3}=\frac{2}{3}\int{{{t}^{2}}\text{dt}}=\frac{2}{9}{{t}^{3}}+C\).
Vậy \(\int{\left( \sqrt{3x+2} \right)}\text{d}x=\frac{2}{9}\left( 3x+2 \right)\sqrt{3x+2}+C\).
Trong không gian với hệ tọa độ Oxyz, đường thẳng \(\Delta \) đi qua điểm \(A\left( -2\,;\,4\,;\,3 \right)\) và vuông góc với mặt phẳng \(\left( \alpha \right):\,2x-3y+6z+19=0\) có phương trình là
Mặt phẳng \(\left( \alpha\right):\,2x-3y+6z+19=0\) có vectơ pháp tuyến là \(\overrightarrow{n}=\left( 2\,;-3\,;\,6 \right)\).
Đường thẳng \(\Delta \) đi qua điểm \(A\left( -2\,;\,4\,;\,3 \right)\) và vuông góc với mặt phẳng \(\left( \alpha \right)\) nhận \(\overrightarrow{n}=\left( 2\,;-3\,;\,6 \right)\) làm vectơ chỉ phương, khi đó phương trình đường thẳng \(\Delta \) là: \(\frac{x+2}{2}=\frac{y-4}{-3}=\frac{z-3}{6}.\)
Cho hàm số \(f\left( x \right)\) có đạo hàm \({f}'\left( x \right)={{x}^{3}}\left( x-1 \right)\left( x-2 \right),\,\forall x\in \mathbb{R}.\) Số điểm cực trị của hàm số đã cho là
Xét \(f'\left( x \right) = {x^3}\left( {x - 1} \right)\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 1\\ x = 2 \end{array} \right.\), ta có bảng biến thiên như sau:
.png)
Dựa vào bảng biến thiên ta kết luận hàm số đã cho có 3 điểm cực trị.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB nằm trong mặt phẳng vuông góc với \(\left( ABCD \right), \widehat{SAB}={{30}^{0}}, SA=2a\). Tính thể tích V của khối chóp S.ABCD.
.png)
Gọi H là hình chiếu vuông góc của S lên cạnh AB.
Do \(\left( SAB \right)\bot \left( ABCD \right)\) và \(\left( SAB \right)\cap \left( ABCD \right)=AB\) nên \(SH\bot \left( ABCD \right).\)
Xét tam giác SAH vuông tại H ta có: \(\sin \widehat{SAB}=\frac{SH}{SA}\Rightarrow SH=\sin {{30}^{0}}.SA=a.\)
Mặt khác: \({{S}_{ABCD}}=A{{D}^{2}}={{a}^{2}}.\)
Nên \({{V}_{S.ABCD}}=\frac{1}{3}\cdot {{S}_{ABCD}}.a=\frac{1}{3}\cdot {{a}^{2}}.a=\frac{{{a}^{3}}}{3}\cdot \)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, \(SA\bot \left( ABCD \right)\). Gọi I là trung điểm của SC. Khoảng cách từ $I$ đến mặt phẳng \(\left( ABCD \right)\) bằng độ dài đoạn thẳng nào?
.png)
Từ giả thiết suy ra OI là đường trung bình của \(\Delta SAC\), do đó \(OI\parallel \,SA\).
Ta có \(\left\{ \begin{array}{l} IO\parallel \,SA\\ SA \bot \left( {ABCD} \right) \end{array} \right. \Rightarrow IO \bot \left( {ABCD} \right)\)
Vậy \(d\left( {I,\left( {ABCD} \right)} \right) = OI\)
Với hai số thực dương \(a,\,b\) thỏa mãn \(\frac{{{\log }_{3}}5{{\log }_{5}}a}{1+{{\log }_{3}}2}-{{\log }_{6}}b=2\). Khẳng định nào dưới đây là khẳng định đúng?
\(\frac{{{{\log }_3}5.{{\log }_5}a}}{{1 + {{\log }_3}2}} - {\log _6}b = 2 \Leftrightarrow \frac{{{{\log }_3}a}}{{{{\log }_3}6}} - {\log _6}b = 2\)
\( \Leftrightarrow {\log _6}a - {\log _6}b = 2 \Leftrightarrow {\log _6}\frac{a}{b} = 2\)
\( \Leftrightarrow \frac{a}{b} = 36 \Leftrightarrow a = 36b\)
Bất phương trình \({{4}^{x-15}}<32\) có bao nhiêu nghiệm nguyên dương?
\({4^{x - 15}} < 32 \Leftrightarrow {2^{2x - 30}} < {2^5}\)
\(\begin{array}{l} \Leftrightarrow 2x - 30 < 5\\ \Leftrightarrow x < \frac{{35}}{2} \end{array}\)
Nghiệm của bất phương trình là \(x<\frac{35}{2}\)
\(\Rightarrow \) Các nghiệm nguyên dương của bất phương trình là: \(x=1;\,2;\,3;\,...... ; 15;\,16;\,17\). Có 17 nghiệm nguyên dương.
Giá trị của tích phân \(I=\int\limits_{0}^{1}{\frac{x}{x+1}}\text{d}x\) là
\(I = \int\limits_0^1 {\frac{x}{{x + 1}}} {\rm{d}}x = \int\limits_0^1 {\left( {1 - \frac{1}{{x + 1}}} \right)} {\rm{d}}x = \int\limits_0^1 {{\rm{d}}x} - \int\limits_0^1 {\frac{1}{{x + 1}}{\rm{d}}\left( {x + 1} \right)} \)
\(= \left. x \right|_0^1 - \left. {\ln \left| {x + 1} \right|} \right|_0^1 = 1 - \ln 2\)
Hàm số \(y=\sqrt{2018x-{{x}^{2}}}\) nghịch biến trên khoảng nào trong các khoảng sau đây?
Tập xác định: \(D=\left[ 0;2018 \right]; {y}'=\frac{2018-2x}{2\sqrt{2018x-{{x}^{2}}}}; {y}'=0\Rightarrow x=1009\).
Bảng biến thiên:
.png)
Hàm số nghịch biến trên khoảng \(\left( 1009\,;2018 \right)\). Do đó hàm số nghịch biến trên \(\left( 1010\,;2018 \right)\).
Tìm số phức z thỏa mãn \(\left( 2-3i \right)z-\left( 9-2i \right)=\left( 1+i \right)z.\)
\(\left( {2 - 3i} \right)z - \left( {9 - 2i} \right) = \left( {1 + i} \right)z \Leftrightarrow \left[ {\left( {2 - 3i} \right) - \left( {1 + i} \right)} \right]z = 9 - 2i \Leftrightarrow z = \frac{{9 - 2i}}{{1 - 4i}} = 1 + 2i.\)
Tổ 1 lớp 11A có 6 nam và 7 nữ; tổ 2 có 5 nam và 8 nữ. Chọn ngẫu nhiên mỗi tổ một học sinh. Xác suất để 2 học sinh được chọn đều là nữ là
Số cách chọn ngẫu nhiên mỗi tổ một học sinh: \(C_{13}^{1}.C_{13}^{1}=169\)
Số phần tử của không gian mẫu: \(n\left( \Omega \right)=169\)
Gọi A là biến cố: “2 học sinh được chọn đều là nữ”.
Số cách chọn ra 2 học sinh đều là nữ: \(C_{7}^{1}.C_{8}^{1}=56\)
Số kết quả thuận lợi cho biến cố A: \(n\left( A \right)=56\)
Xác suất để 2 học sinh được chọn đều là nữ là
\(P\left( A \right)=\frac{n\left( A \right)}{n\left( \Omega \right)}=\frac{56}{169}\).
Trong hình vẽ bên, điểm A biểu diễn số phức \({{z}_{1}}\), điểm B biểu diễn số phức \({{z}_{2}}\) sao cho điểm B đối xứng với điểm A qua gốc tọa độ O. Tìm \(\left| z \right|\) biết số phức \(z={{z}_{1}}+3{{z}_{2}}\).
.jpg.png)
Trong hình trên, ta thấy: Điểm A biểu diễn số phức \({{z}_{1}}=-1+2i\).
Số phức \({{z}_{2}}={{x}_{B}}+{{y}_{B}}i \left( {{x}_{B}}\,,\,{{y}_{B}}\in \mathbb{R} \right)\). Do điểm B biểu diễn số phức \({{z}_{2}}\) và B đối xứng với A qua O, suy ra : \(\left\{ \begin{align} & {{x}_{B}}=-{{x}_{A}}=-\left( -1 \right)=1 \\ & {{y}_{B}}=-{{y}_{A}}=-2 \\ \end{align} \right.\) \(\Rightarrow {{z}_{2}}=1-2i\).
Số phức \(z={{z}_{1}}+3{{z}_{2}}=\left( -1+2i \right)+3.\left( 1-2i \right)=\left( -1+3 \right)+\left( 2-3.2 \right)i=2-4i\).
\(\Rightarrow \left| z \right|=\sqrt{{{2}^{2}}+{{\left( -4 \right)}^{2}}}=2\sqrt{5}\).
Một đường thẳng cắt đồ thị hàm số \(y={{x}^{4}}-2{{x}^{2}}\) tại 4 điểm phân biệt có hoành độ là 0, 1, m và n. Tính \(S={{m}^{2}}+{{n}^{2}}\).
Khi x=0 thì y=0; x=1 thì y=-1.
Suy ra đường thẳng đi qua hai điểm \(O\left( 0;0 \right)\) và \(A\left( 1;-1 \right)\). Véctơ chỉ phương của đường thẳng là \(\overrightarrow{OA}=\left( 1;-1 \right)\), từ đó véctơ pháp tuyến là \(\overrightarrow{n}=\left( 1;1 \right)\).
Vì thế đường thẳng có phương trình \(1.\left( x-1 \right)+1.\left( y-0 \right)=0 \Leftrightarrow x+y=0 \Leftrightarrow y=-x\).
Phương trình hoành độ giao điểm giữa đồ thị hàm số \(y={{x}^{4}}-2{{x}^{2}}\) và đường thẳng y=-x là:
\(\begin{array}{l} {x^4} - 2{x^2} = - x \Leftrightarrow x\left( {{x^3} - 2x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ {x^3} - 2x + 1 = 0 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x = 0\\ \left( {x - 1} \right)\left( {{x^2} + x - 1} \right) = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 1\\ x = \frac{{ - 1 + \sqrt 5 }}{2}\\ x = \frac{{ - 1 - \sqrt 5 }}{2} \end{array} \right. \end{array}\)
Vì thế \(m=\frac{-1+\sqrt{5}}{2}, n=\frac{-1-\sqrt{5}}{2}\) hoặc \(m=\frac{-1-\sqrt{5}}{2}, n=\frac{-1+\sqrt{5}}{2}\).
Vậy \(S={{m}^{2}}+{{n}^{2}}={{\left( \frac{-1+\sqrt{5}}{2} \right)}^{2}}+{{\left( \frac{-1-\sqrt{5}}{2} \right)}^{2}}=3\).
Trong không gian Oxyz, cho hai điểm \(A\left( 2\,;\,3\,;\,-5 \right), B\left( -4\,;\,1\,;\,3 \right)\). Viết phương trình mặt cầu đường kính AB.
Gọi I là trung điểm của AB nên tọa độ của điểm I là: \(I\left( -1\,;\,2\,;\,-1 \right)\).
Vì mặt cầu \(\left( S \right)\) có đường kính là AB nên bán kính mặt cầu \(\left( S \right)\) là:
\(R\,=\,\frac{AB}{2}\,=\,\frac{\sqrt{{{\left( -4\,-\,2 \right)}^{2}}\,+\,{{\left( 1\,-\,3 \right)}^{2}}\,+\,{{\left( 3\,+\,5 \right)}^{2}}}}{2}\,=\,\sqrt{26}\).
Vậy mặt cầu \(\left( S \right)\) có tâm \(I\left( -1\,;\,2\,;\,-1 \right)\) và bán kính \(R\,=\,\sqrt{26}\) có phương trình:
\({{\left( x\,+\,1 \right)}^{2}}\,+\,{{\left( y\,-\,2 \right)}^{2}}\,+\,{{\left( z\,+\,1 \right)}^{2}}\,=\,26\).
Cho hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\) và trục hoành gồm 2 phần, phần nằm phía trên trục hoành có diện tích \({{S}_{1}}=\frac{8}{3}\) và phần nằm phía dưới trục hoành có diện tích \({{S}_{2}}=\frac{5}{12}\). Tính \(I=\int\limits_{-1}^{0}{f\left( 3x+1 \right)\text{d}x}\).
.jpg.png)
Ta có \(\frac{8}{3}={{S}_{1}}=\int\limits_{-2}^{0}{f\left( x \right)\text{d}x};\,\,\,\,\,\,\,\,\,\frac{12}{5}={{S}_{2}}=-\int\limits_{0}^{1}{f\left( x \right)\text{d}x}\Rightarrow \int\limits_{0}^{1}{f\left( x \right)\text{d}x}=-\frac{12}{5}.\)
Tính \(I=\int\limits_{-1}^{0}{f\left( 3x+1 \right)\text{d}x}\)
Đặt \(t=3x+1\Rightarrow \text{d}x=\frac{1}{3}\text{d}t\).
Đổi cận: \(x=-1\Rightarrow t=-2,\,\,x=0\Rightarrow t=1\).
\( \Rightarrow I = \frac{1}{3}\int\limits_{ - 2}^1 {f\left( t \right){\rm{d}}t} = \frac{1}{3}\left( {\int\limits_{ - 2}^0 {f\left( t \right){\rm{d}}t} + \int\limits_0^1 {f\left( t \right){\rm{d}}t} } \right) = \frac{1}{3}\left( {\frac{8}{3} - \frac{5}{{12}}} \right) = \frac{3}{4}.\)
Trong không gian Oxyz, cho điểm \(M(1;\,0;\,1)\) và đường thẳng \(d:\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-3}{3}.\) Đường thẳng đi qua M, vuông góc với d và cắt Oz có phương trình là
Gọi \(\Delta \) là đường thẳng cần tìm và \(N=\Delta \cap Oz.\)
Ta có \(N(0;\,0;\,c).\) Vì \(\Delta \) qua \(M,\,N\) và \(M\notin Oz\) nên \(\overrightarrow{MN}(-1;\,0;\,c-1)\) là VTCP của \(\Delta .\)
d có 1 VTCP \(\vec{u}(1;\,2;\,3)\) và \(\Delta \bot d\) nên
\(\overrightarrow{MN}\cdot \vec{u}=0\Leftrightarrow -1+3(c-1)=0\Leftrightarrow c=\frac{4}{3}\Rightarrow \overrightarrow{MN}(-1;\,0;\,\frac{1}{3}).\)
Chọn \(\vec{v}(-3;\,0;\,1)\) là 1 VTCP của \(\Delta \), phương trình tham số của đường thẳng \(\Delta \) là \(\left\{ \begin{array}{l} x = 1 - 3t\\ y = 0\\ z = 1 + t \end{array} \right.\)
Cho hàm số y=f(x) có đạo hàm tại \(\forall x\in \mathbb{R}\), hàm số \({f}'(x)={{x}^{3}}+a{{x}^{2}}+bx+c\)
Có đồ thị
.jpg.png)
Số điểm cực trị của hàm số \(y=f\left[ {f}'\left( x \right) \right]\) là
Số điểm cực trị bằng số nghiệm đơn (nghiệm bội lẻ) của phương trình đa thức \({g}'\left( x \right)=0\).
PT \({g}'\left( x \right)=0\) có 7 nghiệm phân biệt nên hàm số đã cho có 7 điểm cực trị.
S là tập tất cả các số nguyên dương của tham số m sao cho bất phương trình \({{4}^{x}}-m{{2}^{x}}-m+15>0\) có nghiệm đúng với mọi \(x\in \left[ 1;2 \right]\). Tính số phần tử của S
Đặt \(t={{2}^{x}}\) với \(x\in \left[ 1;2 \right]\) thì \(t\in \left[ 2;4 \right]\)
Bài toán trở thành tìm m để bất phương trình \({{t}^{2}}-mt-m+15>0\) có nghiệm với mọi \(t\in \left[ 2;4 \right]\)
\({{t}^{2}}-mt-m+15>0 \forall t\in \left[ 2;4 \right]\)
\(\Leftrightarrow m<\frac{{{t}^{2}}+15}{t+1} \forall t\in \left[ 2;4 \right]\)
Đặt \(f\left( t \right)=\frac{{{t}^{2}}+15}{t+1}\)
Do đó: \(m<\underset{t\in \left[ 2;4 \right]}{\mathop{\text{max}\,f\left( t \right)}}\,=\frac{19}{3}\)
Vì m nguyên dương nên \(m\in \left\{ 1;2;3;4;5;6 \right\}\)
Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có đáy ABC là tam giác đều cạnh bằng a và \(\left( {A}'BC \right)\) hợp với mặt đáy ABC một góc \(30{}^\circ \). Tính thể tích V của khối lăng trụ \(ABC.{A}'{B}'{C}'\).
.png)
Gọi M là trung điểm của BC. Ta có \(\left\{ {\begin{array}{*{20}{c}} {BC \bot AA'}\\ {BC \bot AM} \end{array}} \right. \Rightarrow BC \bot \left( {A'MA} \right) \Rightarrow BC \bot A'M\)
\( \Rightarrow \widehat {\left( {\left( {A'BC} \right),\left( {ABC} \right)} \right)} = \widehat {A'MA} = 30^\circ \)
Vì \(AB=a\Rightarrow AM=\frac{a\sqrt{3}}{2}.\Rightarrow \tan \widehat{{A}'MA}=\frac{A{A}'}{AM}\Rightarrow A{A}'=\tan \widehat{{A}'BA}.AM=\tan 30{}^\circ .\frac{a\sqrt{3}}{2}=\frac{a}{2}\).
Vậy thể tích của \(ABC.{A}'{B}'{C}'\) là:
\({{V}_{ABC.{A}'{B}'{C}'}}=A{A}'.{{S}_{{A}'{B}'{C}'}}=\frac{a}{2}.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{a}^{3}}\sqrt{3}}{8}\).
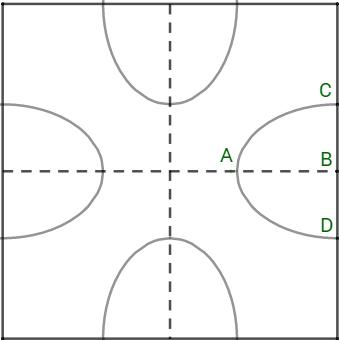
Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh 20cm bằng cách khoét đi bốn phần bằng nhau có hình dạng một nửa elip như hình bên. Biết một nửa trục lớn AB=6cm, trục bé CD=8cm. Diện tích bề mặt hoa văn đó bằng
.jpg.png)
Diện tích của nửa elip có độ dài một nửa trục lớn AB=6cm, trục bé CD=8cm là \(\frac{1}{2}\pi .6.4=12\pi \left( c{{m}^{2}} \right)\).
Diện tích bề mặt hoa văn đó là \(S={{S}_{hinh\_vuong}}-4{{S}_{nua\_elip}}={{20}^{2}}-4.12\pi =400-48\pi \left( c{{m}^{2}} \right)\)
Trên một cánh đồng có 2 con bò được cột vào 2 cây cọc khác nhau. Biết khoảng cách giữa 2 cọc là 4 mét còn 2 sợi dây cột 2 con bò dài 3 mét và 2 mét. Tính phần diện tích mặt cỏ lớn nhất mà 2 con bò có thể ăn chung.
.jpg.png)
Gọi \(\left( {{C_1}} \right):{x^2} + {y^2} = 9 \vee \left( {{C_2}} \right):{\left( {x - 4} \right)^2} + {y^2} = 4\) là phương trình hai đường tròn biểu diễn phần ăn cỏ của 2 con bò.
Xét phần phía trên Ox
\(\begin{array}{l} \left( {{C_1}} \right):{x^2} + {y^2} = 9 \Rightarrow y = \sqrt {9 - {x^2}} \\ \left( {{C_2}} \right):{\left( {x - 4} \right)^2} + {y^2} = 4 \Rightarrow y = \sqrt { - {x^2} + 8x - 12} \end{array}\)
Phương trình hoành độ giao điểm \(\sqrt {9 - {x^2}} = \sqrt { - {x^2} + 8x - 12} \Leftrightarrow x = \frac{{21}}{8}\)
Vậy \(S = 2\left[ {\int\limits_2^{\frac{{21}}{8}} {\sqrt {4 - {{\left( {x - 4} \right)}^2}} } {\rm{d}}x + \int\limits_{\frac{{21}}{8}}^3 {\sqrt {9 - {x^2}} } {\rm{d}}x} \right]\)
\(I = \int\limits_{\frac{{21}}{8}}^3 {\sqrt {9 - {x^2}} } {\rm{d}}x\mathop = \limits^{x = 3\sin t} \int\limits_{\arcsin \frac{7}{8}}^{\frac{\pi }{6}} {9{{\cos }^2}t{\rm{d}}t} = 9.\int\limits_{\arcsin \frac{7}{8}}^{\frac{\pi }{6}} {\frac{{\cos 2t + 1}}{2}{\rm{d}}t = \left. {9\left( {\frac{1}{4}\sin 2t + \frac{t}{2}} \right)} \right|} _{\arcsin \frac{7}{8}}^{\frac{\pi }{6}} \approx 0,3679\)
\(J = \int\limits_2^{\frac{{21}}{8}} {\sqrt {4 - {{\left( {x - 4} \right)}^2}} } {\rm{d}}x\mathop = \limits^{x - 4 = 2\sin t} \int\limits_{ - \frac{\pi }{2}}^{\arcsin \left( { - \frac{{11}}{{16}}} \right)} {4{{\cos }^2}t{\rm{d}}t} = 4.\int\limits_{ - \frac{\pi }{2}}^{\arcsin \left( { - \frac{{11}}{{16}}} \right)} {\frac{{\cos 2t + 1}}{2}{\rm{d}}t = \left. {4\left( {\frac{1}{4}\sin 2t + \frac{t}{2}} \right)} \right|} _{ - \frac{\pi }{2}}^{\arcsin \left( { - \frac{{11}}{{16}}} \right)} \approx 0,627\)
\(\Rightarrow S \approx 1,9898\)
Cho hàm số \(f\left( x \right)\) liên tục trên R và thỏa \(\int\limits_{0}^{3}{f\left( \sqrt{{{x}^{2}}+16}+x \right)\text{d}x=2019,}\int\limits_{4}^{8}{\frac{f\left( x \right)}{{{x}^{2}}}\text{d}x=1.}\) Tính \(\int\limits_4^8 {f\left( x \right){\rm{d}}x} .\)
Xét \({{I}_{1}}=\int\limits_{0}^{3}{f\left( \sqrt{{{x}^{2}}+16}+x \right)\text{d}x=2019}\)
Đặt \(u=\sqrt{{{x}^{2}}+16}+x\Leftrightarrow u-x=\sqrt{{{x}^{2}}+16}\Rightarrow x=\frac{{{u}^{2}}-16}{2u}\Rightarrow \ \text{d}x=\frac{{{u}^{2}}+16}{2{{u}^{2}}}\text{d}u.\)
Khi \(x=0\Rightarrow u=4.\)
Khi \(x=3\Rightarrow u=8.\)
\(\Rightarrow {{I}_{1}}=\frac{1}{2}\int\limits_{4}^{8}{\frac{{{u}^{2}}+16}{{{u}^{2}}}f\left( u \right)\text{d}u=2019}\Rightarrow \int\limits_{4}^{8}{\frac{{{x}^{2}}+16}{{{x}^{2}}}f\left( x \right)\text{d}x=\int\limits_{4}^{8}{\frac{{{u}^{2}}+16}{{{u}^{2}}}f\left( u \right)\text{d}u=4038.}}\)
\(\Rightarrow \int\limits_{4}^{8}{\frac{{{x}^{2}}+16}{{{x}^{2}}}f\left( x \right)\text{d}x}=4038\Leftrightarrow \int\limits_{4}^{8}{f\left( x \right)\text{d}x}+16\int\limits_{4}^{8}{\frac{f\left( x \right)}{{{x}^{2}}}\text{d}x=}4038\Leftrightarrow \int\limits_{4}^{8}{f\left( x \right)\text{d}x}=4038-16=4022.\)
Do \(\int\limits_{4}^{8}{\frac{f\left( x \right)}{{{x}^{2}}}\text{d}x=1}.\)
Kết luận: \(\int\limits_{4}^{8}{f\left( x \right)\text{d}x}=4022.\)
Cho hàm số \(f\left( x \right)=\frac{1}{4}{{x}^{4}}-m{{x}^{3}}+\frac{3}{2}\left( {{m}^{2}}-1 \right){{x}^{2}}+\left( 1-{{m}^{2}} \right)x+2019\) với m là tham số thực. Biết rằng hàm số \(y=f\left( \left| x \right| \right)\) có số điểm cực trị lớn hơn 5 khi \(a<{{m}^{2}}<b+2\sqrt{c}\,\left( a,\,b,\,c\,\in \mathbb{R} \right)\). Tích abc bằng
\(\begin{array}{l} f\left( x \right) = \frac{1}{4}{x^4} - m{x^3} + \frac{3}{2}\left( {{m^2} - 1} \right){x^2} + \left( {1 - {m^2}} \right)x + 2019.\\ \Rightarrow f'\left( x \right) = {x^3} - 3m{x^2} + 3\left( {{m^2} - 1} \right)x + \left( {1 - {m^2}} \right) = g\left( x \right). \end{array}\)
\(\Rightarrow g'\left( x \right)=3{{x}^{2}}-6mx+3\left( {{m}^{2}}-1 \right).\)
\(g'\left( x \right)=0.\)
\(\Leftrightarrow {{x}^{2}}-2mx+\left( {{m}^{2}}-1 \right)=0.\)
\(\Leftrightarrow {{\left( x-m \right)}^{2}}-1=0.\)
\( \Rightarrow \left[ {\begin{array}{*{20}{c}} {x = m + 1.}\\ {x = m - 1.} \end{array}} \right.\)
Hàm số \(y=f\left( \left| x \right| \right)\) có số điểm cực trị lớn hơn 5.
\(\Leftrightarrow \) Hàm số \(y=f\left( x \right)\) có 3 điểm cực trị dương.
\(\Leftrightarrow \) Phương trình \(g\left( x \right)=0\) có 3 nghiệm dương phân biệt.
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m + 1 \ne m - 1}\\ {\begin{array}{*{20}{c}} {m + 1 > 0}\\ {m - 1 > 0}\\ {g\left( {m + 1} \right).g\left( {m - 1} \right) < 0} \end{array}}\\ {g\left( 0 \right) < 0} \end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 1}\\ {\left( {{m^3} - {m^2} - 3m - 1} \right)}\\ {1 - {m^2} < 0} \end{array}} \right.\left( {{m^3} - {m^2} - 3m + 3} \right) < 0\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 1}\\ {\begin{array}{*{20}{c}} {{m^3} - {m^2} - 3m - 1 < 0}\\ {{m^3} - {m^2} - 3m + 3 > 0} \end{array}}\\ {1 - {m^2} < 0} \end{array}} \right.\)
\(\begin{array}{l} \Leftrightarrow \sqrt 3 < m < 1 + \sqrt 2 .\\ \Rightarrow 3 < {m^2} < 3 + 2\sqrt 2 . \end{array}\)
\(\begin{array}{l} \Rightarrow a = b = 3,\,c = 2.\\ \Rightarrow abc = 18\,. \end{array}\)
Cho phương trình: \({{2}^{{{x}^{3}}+{{x}^{2}}-2x+m}}-{{2}^{{{x}^{2}}+x}}+{{x}^{3}}-3x+m=0\). Tập các giá trị để bất phương trình có ba nghiệm phân biệt có dạng \(\left( a\,;\,b \right)\). Tổng a+2b bằng:
Ta có
\({2^{{x^3} + {x^2} - 2x + m}} - {2^{{x^2} + x}} + {x^3} - 3x + m = 0 \Leftrightarrow {2^{{x^3} + {x^2} - 2x + m}} + {x^3} + {x^2} - 2x + m = {2^{{x^2} + x}} + {x^2} + x\,\left( * \right)\)
Xét hàm số \(f\left( t \right)={{2}^{t}}+t\) trên \(\mathbb{R}\)
Ta có: \({f}'\left( t \right)={{2}^{t}}\ln 2+1>0,\,\forall t\in \mathbb{R}\Rightarrow \) Hàm số \(f\left( t \right)\) đồng biến trên \(\mathbb{R}\)
Mà \(\left( * \right)\Leftrightarrow f\left( {{x}^{3}}+{{x}^{2}}-2x+m \right)=f\left( {{x}^{2}}+x \right)\Leftrightarrow {{x}^{3}}+{{x}^{2}}-2x+m={{x}^{2}}+x\)
\(\Leftrightarrow {{x}^{3}}-3x+m=0\Leftrightarrow m=-{{x}^{3}}+3x\,\left( ** \right)\)
Xét hàm số \(g\left( x \right)=-{{x}^{3}}+3x\) trên \(\mathbb{R}\)
Ta có: \({g}'\left( x \right)=-3{{x}^{2}}+3\)
\({g}'\left( x \right)=0\Leftrightarrow x=\pm 1\).
Bảng biến thiên:
.png)
Phương trình \({{2}^{{{x}^{3}}+{{x}^{2}}-2x+m}}-{{2}^{{{x}^{2}}+x}}+{{x}^{3}}-3x+m=0\) có 3 nghiệm phân biệt \(\Leftrightarrow \) phương trình (**) có 3 nghiệm phân biệt \( \Leftrightarrow - 2 < m < 2 \Rightarrow \left\{ \begin{array}{l} a = - 2\\ b = 2 \end{array} \right. \Rightarrow a + 2b = 2\)
Cho số phức z thỏa mãn \(\left| z \right|=2\). Tìm giá trị nhỏ nhất của biểu thức \(P=\left| z-4 \right|+2\left| z-3+2i \right|\).
.png)
Gọi \(M\left( x;\,y \right)\) là điểm biểu diễn cho số phức z, ta có \(\left| z \right|=2 \Leftrightarrow {{x}^{2}}+{{y}^{2}}=4\).
Gọi \(A\left( 4;0 \right), B\left( 3;\,-2 \right)\), khi đó \(P=\left| z-4 \right|+2\left| z-3+2i \right|=MA+2MB\).
Ta có \(MA=\sqrt{{{\left( x-4 \right)}^{2}}+{{y}^{2}}}=\sqrt{{{x}^{2}}+{{y}^{2}}-8x+16} =\sqrt{{{x}^{2}}+{{y}^{2}}-8x+4+3\left( {{x}^{2}}+{{y}^{2}} \right)}=\sqrt{4{{x}^{2}}+4{{y}^{2}}-8x+4} =2\sqrt{{{\left( x-1 \right)}^{2}}+{{y}^{2}}}=2ME\) với \(E\left( 1;\,0 \right)\)
Thấy E nằm trong và B nằm ngoài đường tròn \(\left( C \right): {{x}^{2}}+{{y}^{2}}=4\).
Ta được \(P=MA+2MB=2ME+2MB\ge 2EB\). Dấu bằng xảy ra khi và chỉ khi E, M, B thẳng hàng. Vậy giá trị nhỏ nhất của P bằng \({2EB=2\sqrt{4+4}=4\sqrt{2}}\).
Trong không gian với hệ tọa độ Oxyz, cho hai mặt cầu \(\left( {{S}_{1}} \right),\left( {{S}_{2}} \right)\) lần lượt có phương trình là \({{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x-2y-2z-22=0, {{x}^{2}}+{{y}^{2}}+{{z}^{2}}-6x+4y+2z+5=0\). Xét các mặt phẳng \(\left( P \right)\) thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu đã cho. Gọi \(M\left( a;b;c \right)\) là điểm mà tất cả các \(mp\left( P \right)\) đi qua. Tính tổng S=a+b+c.
.jpg.png)
Mặt cầu \(\left( {{S}_{1}} \right)\) có tâm \({{I}_{1}}=\left( 1;1;1 \right)\), bán kính \({{R}_{1}}=5\)
Mặt cầu \(\left( {{S}_{2}} \right)\) có tâm \({{I}_{2}}=\left( 3;-2;-1 \right)\), bán kính \({{R}_{2}}=3\).
Ta có \(\left| {{R}_{1}}-{{R}_{2}} \right|<{{I}_{1}}{{I}_{2}}=\sqrt{17}<{{R}_{1}}+{{R}_{2}}\) nên hai mặt cầu này cắt nhau.
Do đó mặt phẳng \(\left( P \right)\) tiếp xúc ngoài hai mặt cầu.
Giả sử mặt phẳng \(\left( P \right)\) tiếp xúc \(\left( {{S}_{1}} \right),\left( {{S}_{2}} \right)\) theo thứ tự tại điểm \({{H}_{1}},{{H}_{2}}\).
Gọi \(M={{I}_{1}}{{I}_{2}}\cap \left( P \right)\) theo định lý Talet ta có
\(\frac{{M{I_2}}}{{M{I_1}}} = \frac{{{I_2}{H_2}}}{{{I_1}{H_1}}} = \frac{{{R_2}}}{{{R_1}}} = \frac{3}{5} \Rightarrow \overrightarrow {M{I_2}} = \frac{3}{5}\overrightarrow {M{I_1}} \Leftrightarrow \left\{ \begin{array}{l} 3 - a = \frac{3}{5}\left( {1 - a} \right)\\ - 2 - b = \frac{3}{5}\left( {1 - b} \right)\\ - 1 - c = \frac{3}{5}\left( {1 - c} \right) \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 6\\ b = - \frac{{13}}{2}\\ c = - 4 \end{array} \right.\)
Vậy các mặt phẳng (P) luôn đi qua điểm \(M\left( {6;\frac{{ - 13}}{2}; - 4} \right)\) và \(S = a + b + c = - \frac{9}{2}\).




