Đề thi thử THPT QG năm 2021 môn Vật Lý - Trường THPT Phan Đăng Lưu
Đề thi thử THPT QG năm 2021 môn Vật Lý
-
Hocon247
-
40 câu hỏi
-
90 phút
-
53 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Trong sự truyền sóng cơ, để phân loại sóng ngang và sóng dọc người ta căn cứ vào:
Để phân loại sóng ngang hay sóng dọc người ta dựa vào phương truyền sóng và phương dao động:
Nếu phương dao động trùng với phương truyền sóng thì đó là sóng dọc.
Nếu phương dao dộng vuông góc với phương truyền sóng thì đó là sóng ngang.
Phương trình x=10cos(ωt+φ)cm của vật dao động điều hòa tại thời điểm t nào đó, li độ của vật có thể nhận giá trị nào sau đây:
Ta có: x = 10cos(ωt + φ) (cm) =>
\(\,\left\{ \begin{array}{l}
{x_{\min }} = - 10\left( {cm} \right)\\
{x_{\max }} = 10\left( {cm} \right)
\end{array} \right.\)
Giá trị của x có thể nhận:
\({x_{\min }} \le x \le {x_{\max }} \Leftrightarrow - 10\left( {cm} \right) \le x \le 10\left( {cm} \right)\)
Một con lắc đơn có độ dài l thì dao động điều hòa với chu kì T. Hỏi cũng tại nơi đó nếu tăng gấp đôi chiều dài dây treo và giảm khối lượng của vật đi một nửa thì chu kì sẽ thay đổi như thế nào?
Chu kì dao động của con lắc đơn: không phụ thuộc vào m, chỉ phụ thuộc vào l và g. Do đó khi tăng l gấp đôi thì T tăng √2 lần.
Cho mạch RLC nối tiếp có \({U_L}\; = {\rm{ }}{U_R}\; = {\rm{ }}0,5{U_C}\) thì độ lệch pha giữa hiệu điện thế hai đầu đoạn mạch với dòng điện qua mạch là:
Ta có:
\(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{{U_L} - {U_C}}}{{{U_R}}} = \frac{{0,5{U_C} - {U_C}}}{{0,5{U_C}}} = - 1 \Rightarrow \varphi = - \frac{\pi }{4}\)
=> u trễ pha hơn i một góc π/4
Một chất điểm dddh có tốc độ khi qua vị trí cân bằng là 8π cm/s và độ lớn gia tốc khi ở biên là 16π2 cm/s2 thì biên độ của dao động là:
Vận tốc cực đại:
\({v_{\max }} = \omega A = 8\pi \left( {cm/s} \right)\)
Độ lớn gia tốc khi ở biên: amax = ω2A = 16π2 (cm/s2)
\(\begin{array}{l}
\Rightarrow \omega = \frac{{{a_{\max }}}}{{{v_{\max }}}} = 2\pi (rad/s)\\
\Rightarrow A = \frac{{{v_{\max }}}}{\omega } = 4cm
\end{array}\)
Câu nào đúng. Tia α
Tia anpha là dòng các hạt nhân He có tốc độ khoảng 2.107 m/s, làm ion mạnh môi trường và bay được khoảng 8cm trong không khí.
Vì là dòng các hạt mang điện dương nên khi vào từ trường và điện trường đều bị lệch hướng.
Một nguồn sáng có công suất 10mW phát ra bức xạ đơn sắc có bước sóng λ. Trong một đơn vị thời gian, số photon do nguồn phát ra là 2.1016. Giá trị của λ là:
Năng lượng của một phô-tôn:
\(\begin{array}{l}
\varepsilon = \frac{E}{N} = \frac{{P.t}}{N} = \frac{{{{10.10}^{ - 3}}}}{{{{2.10}^{16}}}} = {5.10^{ - 19}}\\
\varepsilon = \frac{{hc}}{\lambda }\\
\Rightarrow \lambda = \frac{{hc}}{\varepsilon } = \frac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{5.10}^{ - 19}}}} = {3,975.10^{ - 7}}\left( {\rm{m}} \right)
\end{array}\)
Phát biểu nào về ánh sáng sau đây đúng?
+ Mỗi ánh sáng đơn sắc có một màu và tần số nhất định => A đúng
+ Bước sóng ánh sáng rất nhỏ so với bước sóng cơ học => B sai
+ Nếu ánh sáng hỗn hợp chỉ có hai ánh sáng đơn sắc thì không thể tạo thành ánh sáng trắng => C sai.
+ Ánh sáng hỗn hợp cũng có màu những màu đỏ là màu trộn giữa các ánh sáng đơn sắc không phải là màu đơn sắc => D sai
Công thoát electron của KL làm catôt của một tế bào quang điện là 4,5eV. Chiếu vào catôt lần lượt các bức xạ có bước sóng λ1 = 0,25 μm, λ2 = 0,30 μm, λ3 = 0,20 µm, λ4 = 0,36 μm, µ5 = 0,40 µm, λ6 = 0,16 μm. Các bức xạ gây ra được hiện tượng quang điện là:
+ Giới hạn quang điện:
\({\lambda _0} = \frac{{hc}}{A} = \frac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{4,5.1,6.10}^{ - 19}}}} = {2,76.10^{ - 7}}\left( {\rm{m}} \right) = 0,276\left( {\mu m} \right)\)
+ Điều kiện để xảy ra hiện tượng quang điện là: λ <= λ0
Đối với một chất phỏng xạ, sự phóng xạ xảy ra
Quá trình phóng xạ xảy ra tự phát, không bị chi phối bởi các yếu tố bên ngoài như: nhiệt độ, lực, áp suất...
Pin quang điện biến đổi trực tiếp
Pin quang điện biến đổi trực tiếp quang năng thành điện năng.
Khi nói về tia tử ngoại, nhận định nào dưới đây là sai?
Tia γ, tia X, tia tử ngoại, ánh sáng nhìn thấy, tia hồng ngoại đều có chung bản chất là sóng điện từ.
Đoạn mạch điện xoay chiều khi gồm hai phần tử R và C mắc nối tiếp. Tổng trở của mạch được cho bởi công thức
Tổng trở của đoạn mạch RC:
\(Z = \sqrt {{R^2} + Z_C^2} \)
Chiết suất của một môi trường có giá trị
Chiết suât của một môi trường có giá trị khác nhau đối với các ánh sáng khác nhau, lớn nhất đối với ánh sáng có màu tím, nhỏ nhất đối với ánh sáng màu đỏ.
Một CLLX nằm ngang dao động điều hòa với phương trình: \(x = 5\cos \left( {10\pi t + \frac{\pi }{3}} \right)\)(cm). Chiều dài tự nhiên của lò xo là 20 cm. Tính lực đàn hồi của lò xo khi lò xo có chiều dài 23 cm. Biết m = 100g. Lấy π2 = 10.
Khi lò xo có chiều dài 23cm => x = 3cm => Fdh = kx = mω2x = 3 (N)
Tia X không có tính chất nào sau đây:
Tia X có bước sóng nhỏ hơn ánh sáng đỏ nên có tần số lớn hơn.
Khoảng cách giữa hai điểm trên phương truyền sóng gần nhau nhất và dao động cùng pha với nhau gọi là:
+ Khoảng cách giữa hai điểm gần nhau nhất trên phương truyền sóng dao động cùng pha là λ
+ Khoảng cách giữa hai điểm gần nhau nhất trên phương truyền sóng dao động ngược pha là λ/2
Nguyên tắc hoạt động của 1 máy quang phổ dựa trên hiện tượng
Nguyên tắc hoạt động của máy quang phổ dựa trên hiện tượng tán sắc ánh sáng.
Một mạch RLC, cuộn dây thuần cảm được mắc vào mạng điện sinh hoạt 220 V - 50 Hz. Sau 5 giờ hoạt động, công tơ điện cho biết điện năng mạch tiêu thụ là 0,05 kWh. Biết hệ số công suất của mạch là 0,9. Điện trở thuần R gần nhất với giá trị:
+ Điện năng tiêu thụ của đoạn mạch: A = P.t \( \Rightarrow P = \frac{A}{t} = \frac{{{{0,05.10}^3}}}{5} = 10\) (W)
+ Ta có:
\(P = \frac{{{U^2}{{\cos }^2}\varphi }}{R} \Rightarrow R = \frac{{{U^2}{{\cos }^2}\varphi }}{P} = \frac{{{{220}^2}{{.0,9}^2}}}{{10}} = 3920,4\Omega \)
Khi truyền âm từ không khí vào trong nước, kết luận nào không đúng?
Khi âm truyền từ môi trường này sang môi trường khác thì tần số không đổi nhưng bước sóng và tốc độ truyền âm thay đổi.
Vận tốc âm trong không khí < vận tốc âm trong chất lỏng < vận tốc âm trong chất rắn => B sai
Hệ thức đúng trong một mạch dao động LC lí tưởng gồm cuộn cảm thuần có độ tự cảm L mắc nối tiếp với tụ điện có điện dung C đang có dao động điện từ tự do với tần số f là:
Tần số của mạch LC:
\(f = \frac{1}{{2\pi \sqrt {LC} }} \Rightarrow C = \frac{1}{{4{\pi ^2}{f^2}L}}\)
Khi nói về sóng điện từ, điều nào sau đây là sai?
Sóng điện từ không những truyền được trong môi trường vật chất (rắn, lỏng, khí) mà còn truyền được trong cả chân không,
Trong thí nghiệm Y-âng, hai khe được chiếu bằng ánh sáng đơn sắc có bước sóng λ. Nếu tại điểm M trên màn quan sát có vân tối thứ tư (tính từ vân sáng trung tâm) thì hiệu đường đi của ánh sáng từ hai khe S1, S2 đến M có độ lớn bằng:
+ Điểm M là vân tối khi:
\({d_1} - {d_2} = \left( {k + 0,5} \right)\lambda \)
+ Vân tối thứ 4 nên k = 3
=> \({d_1} - {d_2} = 3,5\lambda \)
Tại mặt chất lỏng nằm ngang có hai nguồn sóng O1, O2 cách nhau 24 cm, dao động điều hòa theo phương thẳng đứng với cùng phương trình u = Acosωt. Ở mặt chất lỏng, gọi d là đường vuông góc đi qua trung điểm O của đoạn O1O2. M là điểm thuộc d mà phần tử sóng tại M dao động cùng pha với phần tử sóng tại O, đoạn OM ngắn nhất là 9 cm. Số điểm cực tiểu giao thoa trên đoạn O1O2 là:
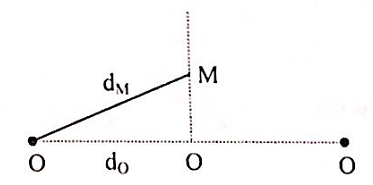
Vì M thuộc trung trực và dao dộng cùng với O nên:
\(\begin{array}{l}
\Rightarrow {d_M} - {d_O} = k\lambda \Rightarrow {d_M} = {d_O} + k\lambda = 12 + k\lambda \\
{d_M} > O{O_1} \Leftrightarrow 12 + k\lambda > 12 \Rightarrow k > 0\\
\Rightarrow {k_{\min }} = 1 \Rightarrow O{M_{\min }} = \sqrt {{{\left( {12 + \lambda } \right)}^2} - {{12}^2}} = 9\\
\Rightarrow \lambda = 3\left( {{\rm{cm}}} \right)
\end{array}\)
So cực tiểu trên O1O2:
\(\begin{array}{l}
- \frac{{{O_1}{O_2}}}{\lambda } - \frac{1}{2} < k < \frac{{{O_1}{O_2}}}{\lambda } - \frac{1}{2}\\
\Leftrightarrow - \frac{{24}}{3} - \frac{1}{2} < k < \frac{{24}}{3} - \frac{1}{2}\\
\Leftrightarrow - 8,5 < k < 7,5
\end{array}\)
Có 16 giá trị
Nguồn âm điểm O phát sóng âm đẳng hướng ra môi trường không hấp thụ và không phản xạ. Điểm M cách nguồn âm một quãng R có mức cường độ âm 20 dB. Tăng công suất nguồn ầm lên n lần thì mức cường độ âm tại N cách nguồn là 30 dB. Giá trị của n là:
+ Mức cường độ âm lúc đầu tại M:
\({L_M} = 10\lg \frac{{{I_M}}}{{{I_0}}} = 20 \Rightarrow \frac{{{I_M}}}{{{I_0}}} = {10^2} \Rightarrow {I_M} = {10^2}{I_0}(1)\)
+ Mức cường độ âm tại N khi tăng công suất gấp n lần:
\({L_N} = 10\lg \frac{{{I_N}}}{{{I_0}}} = 30 \Rightarrow \frac{{{I_N}}}{{{I_0}}} = {10^3} \Rightarrow {I_N} = {10^3}{I_0}\)
+ Lấy (2) chia (1), ta có:
\(\begin{array}{l}
\frac{{{I_N}}}{{{I_M}}} = 10\\
\left\{ \begin{array}{l}
{I_M} = \frac{P}{{4\pi {R^2}}}\\
{I_N} = \frac{{nP}}{{4\pi {{\left( {R/2} \right)}^2}}}
\end{array} \right. \Rightarrow 4n = 10 \Rightarrow n = 2,5
\end{array}\)
Một sóng dừng trên sợi dây đàn hồi dài với bước sóng 60 cm. Ba điểm theo đúng thứ tự E, M và N trên dây (EM = 3MN = 30 cm) và M là điểm bụng. Khi vận tốc dao động tại N là √3 cm/s thì vận tốc dao động tại E là:

Vì M là bụng và EM = 30 = λ/2 => E là bụng liền kề
+ Vì MN = 10 cm = λ/6 => điểm N cách nút O đoạn λ/12
+ Chọn gốc tọa độ tại nút O, phương trình sóng dừng có dạng:
\(\begin{array}{l}
u = 2a\sin \frac{{2\pi x}}{\lambda }\cos \left( {\omega t + \varphi } \right)\\
\Rightarrow v = {u^/} = - \omega .2a\sin \frac{{2\pi x}}{\lambda }\sin \left( {\omega t + \varphi } \right)\\
\frac{{{v_N}}}{{{v_E}}} = \frac{{2a\sin \frac{{2\pi .\frac{\lambda }{{12}}}}{\lambda }}}{{2a\sin \frac{{2\pi \left( {\frac{\lambda }{2} + \frac{\lambda }{4}} \right)}}{\lambda }}}\\
\Leftrightarrow \frac{{\sqrt 3 }}{{{v_E}}} = \frac{{0,5}}{{ - 1}} \Rightarrow {v_E} = - 2\sqrt 3
\end{array}\)
Tự cảm 20 μΗ và một tụ xoay có điện dung (điện dung là hàm bậc nhất của góc xoay) biến thiên từ 10 pF đến 500 pF khi góc xoay biến thiên từ 0° đến 180°. Khi góc xoay bằng 90° thì mạch thu sóng có bước sóng bằng bao nhiêu?
+ Vì C làm hàm bậc nhất của α nên: C = aα + b (*)
Khi α = 0 thì C = 10 pF. Thay vào (*) => b = 10 pF
Khi α = 180° thì C = 500 pF. Thay vào (*) => a = 49/18
Vây, biểu thức của C theo α là: C = 49/18α +10 (pF) (**)
+ Khi α = 90° thay vào (**) ta có: C = 255 pF
+ Bước sóng thu được khi α = 90°: λ = 2πc √LC = 134,54 m
Trong thí nghiệm Y-âng về giao thoa với ánh sáng đơn sắc có bước sóng λ, khoảng cách giữa hai khe hẹp là a, khoảng cách tử mặt phẳng chứa hai khe hẹp đến màn quan sát là 2 m. Trên màn quan sát, tại điểm M cách vân sáng trung tâm 6 mm, có vân sáng bậc 5. Khi thay đổi khoảng cách giữa hai khe hẹp một đoạn bằng 0,2 mm sao cho vị trí vân sáng trung tâm không thay đổi thì tại M có vân sáng bậc 6. Giá trị của λ bằng:
Vị trí vân sáng:
\(x = k\frac{{\lambda D}}{a}\)
+ Nhận thấy k tỉ lệ thuận với a
\( \Rightarrow \left\{ \begin{array}{l}
x = 5\frac{{\lambda D}}{a}\\
x = 6\frac{{\lambda D}}{{a + 0,2}}
\end{array} \right. \Rightarrow \frac{5}{a} = \frac{6}{{a + 0,2}} \Rightarrow a = 1\left( {{\rm{mm}}} \right)\)
+ Lại có:
\(x = 5\frac{{\lambda D}}{a} \Rightarrow \lambda = \frac{{a.x}}{{5D}} = \frac{{1.6}}{{6.2}} = 0,6\left( {\mu m} \right)\)
Nguyên tử hidro ở trạng thái cơ bản có bán kính r0 = 5,3.10-11 m. Coi electron chuyển động tròn đều quanh hạt nhân. Cường độ dòng điện do chuyển động của electron trên quỹ đạo K gây ra là:
Khi e chuyển động trên quỹ đạo n nào đó thì nó chuyển động tròn đều => cường độ dòng điện không đổi.
+Do đó:
\(I = \frac{{\Delta q}}{{\Delta t}} = \frac{q}{T} = \frac{{q\omega }}{{2\pi }} = \frac{{e.\omega }}{{2\pi }}\)
+ Lực tương tác giữa e và hạt nhân là lực điện, lực này đóng vai trò là lực hướng tâm nên:
\({F_d} = {F_{ht}} \Leftrightarrow \frac{{k{e^2}}}{{r_n^2}} = m\frac{{{v^2}}}{{{r_n}}} \Rightarrow \frac{{k{e^2}}}{{r_n^2}} = m{\omega ^2}{r_n}\)
\( \Rightarrow \omega = e\sqrt {\frac{k}{{m.r_n^3}}} \Rightarrow I = \frac{{{e^2}}}{{2\pi }}\sqrt {\frac{k}{{m.r_n^3}}} I = \frac{{{e^2}}}{{2\pi }}\sqrt {\frac{k}{{m.r_0^3}}} \approx {1,05.10^{ - 3}}\) A
Hạt α có động năng 5,3 MeV bắn vào hạt nhân Be9 đứng yên, gây ra phản ứng α +Be9 → n + X. Biết phản ứng tỏa một năng lượng 5,7 MeV và động năng của hạt X lớn gấp 10 lần động năng hạt n. Tính động năng của hạt nhân X tạo thành
Ta có:
\( \Rightarrow 5,7 = \left( {\frac{1}{{10}} + 1} \right){W_X} - 5,3 \Rightarrow {W_X} = 10\left( {MeV} \right)\)
Năng lượng liên kết là năng lượng tỏa ra khi tạo thành một hạt nhân nguyên tử từ các nuclon rời rạc. Tính năng lượng tỏa ra khi các nuclon tạo thành 1 mol heli. Biết hạt He có khối lượng hạt nhân là 4,0015u, mp = l,0073u, mu = 1,0087u, 1uc2 = 931,5 MeV, ΝA= 6,023.1023 hạt/mol.
Năng lượng tỏa ra khi tạo thành 1 hạt: \({W_{lk}} = \Delta m{c^2}\).
Năng lượng tỏa ra khi tạo được 1 mol:
\({W_0} = {N_A}.{W_{lk}} = {1,71.10^{25}}\left( {MeV} \right)\)
Một bệnh nhân điều trị bằng đồng vị phóng xạ, dùng tia γ để diệt tế bào bệnh. Thời gian chiếu xạ lần đầu là Δt0 = 15 phút, cứ sau 1 tháng thì bệnh nhân phải tới bệnh viện khám bệnh và tiếp tục chiếu xạ. Biết đồng vị phóng xạ đó có chu kỳ bán rã T = 4 tháng (coi Δt < T) và vẫn dùng nguồn phóng xạ trong lần đầu. Hỏi lần chiếu xạ thứ 5 phải tiến hành trong bao lâu để bệnh nhân được chiếu xạ với cùng một lượng tia γ như lần đầu?
Thời gian chiếụ xạ lần thứ n: \(\Delta t = \Delta {t_0}{.2^{\frac{t}{T}}}\)
Sau lần chiếu xạ thứ nhất thì cứ sau 1 tháng bệnh nhân lại đi chiếu xạ nên khi chiếu lần thứ 5 thì vào thời điểm t = 4 tháng, Do đó ta có: Δt = 15.2 = 30 phút
Đoạn mạch AB gồm cuộn cảm thuần nối tiếp với tụ điện. Đặt nguồn xoay chiều có tần số góc ω vào hai đầu A và B thì cuộn cảm có cảm kháng 100 Ω, tụ điện có dung kháng 50 Ω. Ngắt A, B ra khỏi nguồn và tăng độ tự cảm một lượng ΔL= 0,5 H rồi nối A và B thành mạch kín thì tần số góc dao động riêng của mạch là 100 (rad/s). Tính ω.
+ Lúc đầu, mắc AB vào nguồn xoay chiều:
\(\left\{ \begin{array}{l}
{Z_L} = \omega L = 100\\
{Z_C} = \frac{1}{{\omega C}} = 50
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
L = \frac{{100}}{\omega }\\
C = \frac{1}{{50\omega }}
\end{array} \right.\) (1)
+ Sau khi tăng L thêm 0,5H rồi nối kín L và C để thành mạch dao động LC thì:
\(\begin{array}{l}
\omega _{LC}^2 = \frac{1}{{\left( {L + 0,5} \right)C}} \Leftrightarrow LC + 0,5C = \frac{1}{{{{100}^2}}}\frac{{100}}{\omega }.\frac{1}{{50\omega }} + 0,5.\frac{1}{{50\omega }} = \frac{1}{{{{100}^2}}}\\
\Rightarrow \frac{2}{{{\omega ^2}}}.\frac{1}{{100}}.\frac{1}{\omega } - \frac{1}{{{{100}^2}}} = 0 \Rightarrow \frac{1}{\omega } = \frac{1}{{200}} \Rightarrow \omega = 200
\end{array}\)
Một con lắc đơn có khối lượng m = 0,5 kg, chiều dài l = 0,5m dao động với biên độ 0°. Do ma sát sau 5 chu kì dao động biên độ chỉ còn 4°. Tính năng lượng của con lắc đơn bị hao hụt trong 5 chu kì nói trên. Lấy g = 9,8m/s2.
Ta có:
\(\Delta W = W - {W_5} = \frac{1}{2}mg\ell \left( {\alpha _{01}^2 - \alpha _{05}^2} \right)\)
Thay số, ta có:
\(\Delta W = \frac{1}{2}.0,5.9,8.0,5\left[ {{{\left( {\frac{{5\pi }}{{180}}} \right)}^2} - {{\left( {\frac{{4\pi }}{{180}}} \right)}^2}} \right] = {3,36.10^{ - 3}}\left( J \right)\)
Đặt điện áp u = U√2cos(ωt), (U, ω không đổi) vào hai đầu đoạn mạch R, L, C. Cuộn dây thuần cảm có L thay đổi được. Điều chỉnh L thì thấy, ở thời điểm điện áp hiệu dụng UR đạt giá trị cực đại thì URmax = UL. Hỏi ở thời điểm điện áp hiệu dụng UL đạt cực đại thì tỉ số ULmax/URmax bằng bao nhiêu?
Khi L thay đổi để UR = max thì \(\left\{ \begin{array}{l}
{Z_{L1}} = {Z_C}\\
{U_{R - \max }} = U
\end{array} \right.\)
+ Mặt khác theo đề khi đó: \({U_{R\max }} = {U_L} \Leftrightarrow R = {Z_{L1}} \Rightarrow R = {Z_C}\) (1)
+ Khi L thay đổi để ULmax thì:
\({U_{L\max }} = \frac{U}{R}\sqrt {{R^2} + Z_C^2} {U_{L\max }} = \frac{U}{R}\sqrt {{R^2} + {R^2}} = U\sqrt 2 \)
+ Vậy, tỉ số: \(\frac{{{U_{L\max }}}}{{{U_{R\max }}}} = \sqrt 2 \)
Hai dao động điều hòa cùng phương theo phương trình: \({x_1} = {A_1}\cos \left( {\omega t + {\varphi _1}} \right)cm;{x_2} = {A_2}\cos \left( {\omega t + {\varphi _2}} \right)\) (cm) trên hình vẽ đường đồ thị (I) biểu diễn dao động thứ nhất, đường đồ thị (II) biểu diễn dao động tổng hợp của hai dao động. Phương trình vận tốc của dao động thứ hai là:
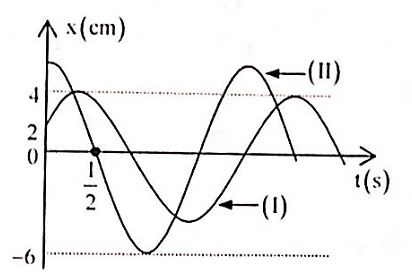
+ Lúc t = 0 dao động II ở biên, đến thời điểm t = 0,5 s thì dao động II ở VTCB nên:
\(\frac{T}{4} = 0,5 \Rightarrow T = 2\left( s \right) \Rightarrow \omega = \pi \) (rad/s)
+ Lúc t = 0, dao động II đang ở biên nên phương trình dao động tổng hợp là:
x = 6cos πt (cm)
+ Lúc t = 0, vật I đang ở \(\left\{ \begin{array}{l}
{x_1} = 2\left( {cm} \right) = \frac{A}{2}\\
{v_1} > 0
\end{array} \right.\) nên phương trình dao động 1 là:
\({x_1} = 4\cos \left( {\pi t - \frac{\pi }{3}} \right)\) (cm)
+ Phương trình dao động thứ 2 là:
\(\begin{array}{l}
x = {x_1} + {x_2}\\
\Rightarrow {x_2} = x - {x_1} = 6\cos \pi t - 4\cos \left( {\pi t - \frac{\pi }{3}} \right) = 2\sqrt 7 \cos \left( {\pi t + 0,714} \right)\\
\Rightarrow {v_2} = {\left( {{x_2}} \right)^/} = 2\pi \sqrt 7 \cos \left( {\pi t + 0,714 + \frac{\pi }{2}} \right)
\end{array}\)
Có ba máy biến áp lý tưởng cuộn thứ cấp của các máy có số vòng dây bằng nhau. Số vòng dây ở cuộn sơ cấp của máy 2 nhiều hơn số vòng dây ở cuộn sơ cấp của máy 1 là x vòng, nhưng lại ít hơn số vòng dây ở cuộn sơ cấp của máy 3 là 2x vòng. Nếu lần lượt mắc vào cuộn sơ cấp của máy 1 máy 2 và máy 3 một điện áp xoay chiều có giá trị hiệu dụng không đổi U thì điện áp hiệu dụng ở hai đầu cuộn thứ cấp để hở của máy 1, máy 2 và máy 3 lần lượt là 60 V, 45V và U3. Giá trị U3 bằng:
Gọi N1 là số vòng dây ở cuộn sơ cấp của máy 1 => số vòng dây ở cuộn sơ cấp các máy 2 và 3 lần lượt là N1 + x, N1 + 3x. Số vòng dây ở cuộn thứ cấp của các máy là N.
Ta có:
\(\left\{ {\begin{array}{*{20}{c}}
{\left. \begin{array}{l}
\frac{{60}}{U} = \frac{N}{{{N_1}}}\\
\frac{{45}}{U} = \frac{N}{{{N_1} + x}}
\end{array} \right\} \Rightarrow \frac{{60}}{{45}} = \frac{{{N_1} + x}}{{{N_1}}} \Rightarrow {N_1} = 3x}\\
{\frac{{{U_3}}}{U} = \frac{N}{{{N_1} + 3x}}}
\end{array}} \right.\)
+ Suy ra:
\(\frac{{{U_3}}}{U} = \frac{N}{{{N_1} + {N_1}}} = \frac{N}{{2{N_1}}}\frac{{{U_3}}}{U} = \frac{1}{2}\frac{{60}}{U} \Rightarrow {U_3} = 30\left( V \right)\)
Một chất điểm dao động với phương trình x = 10cos2πt (cm). Kể từ lúc t = 0 đến lúc vật đi qua vị trí x = 5cm lần thứ 2015 thì thời gian để vectơ vận tốc và vectơ gia tốc cùng hướng theo chiều âm là:
Lúc t = 0 => x0 = 10 cm => vật đang ở biên dương.
+ Một chu kì vật qua x = 5 √3 được 2 lần nên ta xét tỉ số: 2015/2=1007,5
+ Sau 1007Τ vật đã qua x = 5 được 2014 lần còn thiếu 1 lần nên đi thêm T/6 như hình.
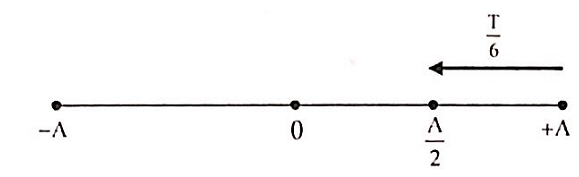
+ Vì 1T có T/4 để a và v cùng hướng âm => sau 1007T có 1007T/4 mà a và v cùng hướng âm. Mặt khác trong thời gian T/6 cuối cùng a và v lại cùng hướng âm nên tổng cả là: t=1007T/4+T/6=3023/12(s)
Mạch xoay chiều AB gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C thay đổi được mắc theo đúng thứ tự trên. Điểm M nằm giữa cuộn cảm và tụ điện. Đặt vào hai đầu mạch một điện áp xoay chiều u = U √2cosωt (V) (R, L, U, ω có giá trị không đổi). Điều chỉnh điện dung của tụ điện sao cho điện áp hiệu dụng hai đầu MB đạt cực đại, khi đó điện áp hiệu dụng hai đầu điện trở R là 150V, điện áp tức thời hai đầu mạch là 150√6V, điện áp tức thời hai đầu mạch AM là 50√6V. Giá trị của U là:
Khi UC = max thì
\({u_{RL}} \bot u \Rightarrow {\left( {\frac{{{u_{RL}}}}{{{U_{0RL}}}}} \right)^2} + {\left( {\frac{u}{{{U_0}}}} \right)^2} = 1 \Leftrightarrow {\left( {\frac{{{u_{RL}}}}{{{U_{RL}}}}} \right)^2} + {\left( {\frac{u}{U}} \right)^2} = 2\)
Thay số ta có: \(\frac{{{{50}^2}.6}}{{U_{RL}^2}} + \frac{{{{150}^2}.6}}{{{U^2}}} = 2\) (1)
+ Mặt khác, lúc đó theo giản đồ vectơ, ta có:
\(\frac{1}{{U_R^2}} = \frac{1}{{U_{RL}^2}} + \frac{1}{{{U^2}}} \Leftrightarrow \frac{1}{{U_{RL}^2}} + \frac{1}{{{U^2}}} = \frac{1}{{{{150}^2}}}\) (2)
+ Giải (1) và (2) ta có: U = 300V
Lần lượt đặt vào 2 đầu đoạn mạch RLC nối tiếp (R là biến trở, L thuần cảm) hai điện áp xoay chiều: u1 = U01cos(ω1t + π) (V) và u2 = U02cos(ω2t - 1,57) (V), người ta thu được đồ thị công suất của mạch điện xoay chiều theo biến trở R như hình bên. Biết A là đỉnh của đồ thị P(2). Giá trị của x gần nhất với giá trị nào sau đây:
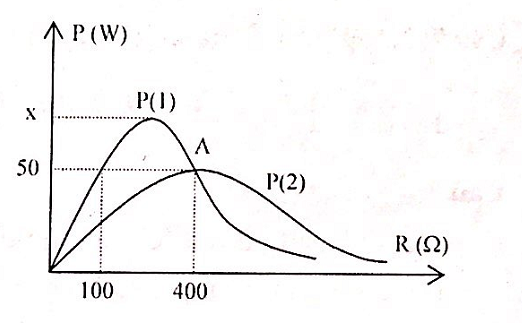
Xét với ω1 tại R1 = 100Ω và R2 = 400Ω thì P1 cho cùng công suất nên:
\(\left\{ \begin{array}{l}
{\left( {{Z_{L1}} - {Z_{C1}}} \right)^2} = {R_1}{R_2} = 40000\\
\frac{{U_1^2}}{{{P_1}}} = {R_1} + {R_2} \Rightarrow U_1^2 = 25000
\end{array} \right.\)
+ Vì X là công suất lớn nhất ứng với P1 nên ta có:
\(x = \frac{{U_1^2}}{{2\left| {{Z_{L1}} - {Z_{C1}}} \right|}} = \frac{{25000}}{{2.\sqrt {40000} }} = 62,5\left( {\rm{W}} \right)\)

