Ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaada % qadaqaaiaaikdacaWGHbGaamiEaiabgUcaRiaadkgaaiaawIcacaGL % PaaacaqGKbGaamiEaaWcbaGaaGymaaqaaiaaikdaa0Gaey4kIipaki % abg2da9maabmaabaGaamyyaiaadIhadaahaaWcbeqaaiaaikdaaaGc % cqGHRaWkcaWGIbGaamiEaaGaayjkaiaawMcaamaaeeaaeaqabeaaca % aIYaaabaGaaGymaaaacaGLhWoacqGH9aqpcaaI0aGaamyyaiabgUca % RiaaikdacaWGIbGaeyOeI0YaaeWaaeaacaWGHbGaey4kaSIaamOyaa % GaayjkaiaawMcaaiabg2da9iaaiodacaWGHbGaey4kaSIaamOyaaaa % !5BB5! \int\limits_1^2 {\left( {2ax + b} \right){\rm{d}}x} = \left( {a{x^2} + bx} \right)\left| \begin{array}{l} 2\\ 1 \end{array} \right. = 4a + 2b - \left( {a + b} \right) = 3a + b\)

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9iGacYgacaGGVbGaai4z % amaaBaaaleaacaaIYaaabeaakmaabmaabaGaaG4maiaadIhacqGHsi % slcaaIXaaacaGLOaGaayzkaaaaaa!4318! f\left( x \right) = {\log _2}\left( {3x - 1} \right)\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Tabm % OzayaafaWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyypa0ZaaSaa % aeaacaaIZaaabaWaaeWaaeaacaaIZaGaamiEaiabgkHiTiaaigdaai % aawIcacaGLPaaaciGGSbGaaiOBaiaaikdaaaaaaa!452C! \Rightarrow f'\left( x \right) = \frac{3}{{\left( {3x - 1} \right)\ln 2}}\)

Gọi x là cạnh của đáy hộp.

h là chiều cao của hộp.

S(x) là diện tích phần hộp cần mạ.

Khi đó, khối lượng vàng dùng mạ tỉ lệ thuận với S.

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 % qacaWGtbWdamaabmaabaWdbiaadIhaa8aacaGLOaGaayzkaaWdbiab % g2da9iaadIhapaWaaWbaaSqabeaapeGaaGOmaaaakiabgUcaRiaais % dacaWG4bGaamiAa8aadaqadaqaa8qacaaIXaaapaGaayjkaiaawMca % aaaa!42C0! S\left( x \right) = {x^2} + 4xh\left( 1 \right)\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 % qacaGG7aGaamOvaiabg2da9iaadIhapaWaaWbaaSqabeaapeGaaGOm % aaaakiaadIgacqGH9aqpcaaI0aGaeyypa0JaeyOpa4JaamiAaiabg2 % da9iaaisdacaGGVaGaamiEa8aadaahaaWcbeqaa8qacaaIYaaaaOWd % amaabmaabaWdbiaaikdaa8aacaGLOaGaayzkaaWdbiaac6caaaa!4829! ;V = {x^2}h = 4 = > h = 4/{x^2}\left( 2 \right).\)

Từ (1) và (2), ta có  \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCa % aaleqabaGaaGOmaaaakiabgUcaRmaalaaabaGaaGymaiaaiAdaaeaa % caWG4baaaaaa!3B4E! S (x)={x^2} + \frac{{16}}{x}\)

Dựa vào BBT, ta có S(x) đạt GTNN khi  x = 2.

Mệnh đề đúng là M = f(0)

Ta có d cắt  mặt phẳng (Oyz) tại \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamytaiabgk % DiElaad2eadaqadaqaaiaaicdacaGG7aWaaSaaaeaacaaI1aaabaGa % aGOmaaaacaGG7aGaeyOeI0YaaSaaaeaacaaI3aaabaGaaGOmaaaaai % aawIcacaGLPaaaaaa!41BB! M \Rightarrow M\left( {0;\frac{5}{2}; - \frac{7}{2}} \right)\), chọn \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaabm % aabaGaeyOeI0IaaG4maiaacUdacaaIXaGaai4oaiaaigdaaiaawIca % caGLPaaacqGHiiIZcaWGKbaaaa!3F4E! A\left( { - 3;1;1} \right) \in d\) và gọi B là hình chiếu vuông góc của A lên mặt phẳng (Oyz)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % OqamaabmaabaGaaGimaiaacUdacaaIXaGaai4oaiaaigdaaiaawIca % caGLPaaaaaa!3E4F! \Rightarrow B\left( {0;1;1} \right)\).

Lại có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8Haaeaaca % WGcbGaamytaaGaay51GaGaeyypa0ZaaeWaaeaacaaIWaGaai4oamaa % laaabaGaaG4maaqaaiaaikdaaaGaai4oaiabgkHiTmaalaaabaGaaG % yoaaqaaiaaikdaaaaacaGLOaGaayzkaaaaaa!420D! \overrightarrow {BM} = \left( {0;\frac{3}{2}; - \frac{9}{2}} \right)\) . Khi đó, vectơ chỉ phương của đường thẳng cần tìm sẽ cùng phương với vectơ \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8Haaeaaca % WGcbGaamytaaGaay51Gaaaaa!3941! \overrightarrow {BM} \)

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiaacE % cadaqadaqaaiaadIhaaiaawIcacaGLPaaacqGH9aqpdaWcaaqaaiab % gkHiTiaaiodaaeaadaqadaqaaiaadIhacqGHsislcaaIYaaacaGLOa % GaayzkaaWaaWbaaSqabeaacaaIYaaaaaaakiaaywW7cqGHaiIicaWG % 4bGaeyiyIKRaaGOmaaaa!47E2! y'\left( x \right) = \frac{{ - 3}}{{{{\left( {x - 2} \right)}^2}}}\quad \forall x \ne 2\). Gọi I là giao của hai tiệm cận nên I(2;1)

Gọi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamytamaabm % aabaGaamiEamaaBaaaleaacaaIWaaabeaakiaacUdacaWG5bWaaSba % aSqaaiaaicdaaeqaaaGccaGLOaGaayzkaaGaeyypa0Jaamytamaabm % aabaGaamiEamaaBaaaleaacaaIWaaabeaakiaacUdadaWcaaqaaiaa % dIhadaWgaaWcbaGaaGimaaqabaGccqGHRaWkcaaIXaaabaGaamiEam % aaBaaaleaacaaIWaaabeaakiabgkHiTiaaikdaaaaacaGLOaGaayzk % aaGaeyicI48aaeWaaeaacaWGdbaacaGLOaGaayzkaaaaaa!4DFA! M\left( {{x_0};{y_0}} \right) = M\left( {{x_0};\frac{{{x_0} + 1}}{{{x_0} - 2}}} \right) \in \left( C \right)\)

Khi đó tiếp tuyến tại \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamytamaabm % aabaGaamiEamaaBaaaleaacaaIWaaabeaakiaacUdacaWG5bWaaSba % aSqaaiaaicdaaeqaaaGccaGLOaGaayzkaaaaaa!3CE8! M\left( {{x_0};{y_0}} \right)\) có phương trình:

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyiLdqKaai % OoaiaaysW7caWG5bGaeyypa0JaamyEaiaacEcadaqadaqaaiaadIha % daWgaaWcbaGaaGimaaqabaaakiaawIcacaGLPaaadaqadaqaaiaadI % hacqGHsislcaWG4bWaaSbaaSqaaiaaicdaaeqaaaGccaGLOaGaayzk % aaGaey4kaSIaamyEamaaBaaaleaacaaIWaaabeaaaaa!48EE! \Delta :\;y = y'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % yEaiabg2da9maalaaabaGaeyOeI0IaaG4maaqaamaabmaabaGaamiE % amaaBaaaleaacaaIWaaabeaakiabgkHiTiaaikdaaiaawIcacaGLPa % aadaahaaWcbeqaaiaaikdaaaaaaOWaaeWaaeaacaWG4bGaeyOeI0Ia % amiEamaaBaaaleaacaaIWaaabeaaaOGaayjkaiaawMcaaiabgUcaRm % aalaaabaGaamiEamaaBaaaleaacaaIWaaabeaakiabgUcaRiaaigda % aeaacaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaeyOeI0IaaGOmaaaaaa % a!4F91! \Leftrightarrow y = \frac{{ - 3}}{{{{\left( {{x_0} - 2} \right)}^2}}}\left( {x - {x_0}} \right) + \frac{{{x_0} + 1}}{{{x_0} - 2}}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aaS % aaaeaacqGHsislcaaIZaaabaWaaeWaaeaacaWG4bWaaSbaaSqaaiaa % icdaaeqaaOGaeyOeI0IaaGOmaaGaayjkaiaawMcaamaaCaaaleqaba % GaaGOmaaaaaaGccaGGUaGaamiEaiabgkHiTiaadMhacqGHRaWkdaWc % aaqaaiaaiodacaWG4bWaaSbaaSqaaiaaicdaaeqaaaGcbaWaaeWaae % aacaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaeyOeI0IaaGOmaaGaayjk % aiaawMcaamaaCaaaleqabaGaaGOmaaaaaaGccqGHRaWkdaWcaaqaai % aadIhadaWgaaWcbaGaaGimaaqabaGccqGHRaWkcaaIXaaabaGaamiE % amaaBaaaleaacaaIWaaabeaakiabgkHiTiaaikdaaaGaeyypa0JaaG % imaaaa!5735! \Leftrightarrow \frac{{ - 3}}{{{{\left( {{x_0} - 2} \right)}^2}}}.x - y + \frac{{3{x_0}}}{{{{\left( {{x_0} - 2} \right)}^2}}} + \frac{{{x_0} + 1}}{{{x_0} - 2}} = 0\)

Khi đó ta có:\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizamaabm % aabaGaamysaiaacUdacqGHuoaraiaawIcacaGLPaaacqGH9aqpdaWc % aaqaamaaemaabaWaaSaaaeaacqGHsislcaaI2aaabaWaaeWaaeaaca % WG4bWaaSbaaSqaaiaaicdaaeqaaOGaeyOeI0IaaGOmaaGaayjkaiaa % wMcaamaaCaaaleqabaGaaGOmaaaaaaGccqGHsislcaaIXaGaey4kaS % YaaSaaaeaacaaIZaGaamiEamaaBaaaleaacaaIWaaabeaaaOqaamaa % bmaabaGaamiEamaaBaaaleaacaaIWaaabeaakiabgkHiTiaaikdaai % aawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaaaaOGaey4kaSYaaSaa % aeaacaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaey4kaSIaaGymaaqaai % aadIhadaWgaaWcbaGaaGimaaqabaGccqGHsislcaaIYaaaaaGaay5b % SlaawIa7aaqaamaakaaabaGaaGymaiabgUcaRmaalaaabaGaaGyoaa % qaamaabmaabaGaamiEamaaBaaaleaacaaIWaaabeaakiabgkHiTiaa % ikdaaiaawIcacaGLPaaadaahaaWcbeqaaiaaisdaaaaaaaqabaaaaa % aa!6352! d\left( {I;\Delta } \right) = \frac{{\left| {\frac{{ - 6}}{{{{\left( {{x_0} - 2} \right)}^2}}} - 1 + \frac{{3{x_0}}}{{{{\left( {{x_0} - 2} \right)}^2}}} + \frac{{{x_0} + 1}}{{{x_0} - 2}}} \right|}}{{\sqrt {1 + \frac{9}{{{{\left( {{x_0} - 2} \right)}^4}}}} }}\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % izamaabmaabaGaamysaiaacUdacqGHuoaraiaawIcacaGLPaaacqGH % 9aqpdaWcaaqaamaaemaabaGaaGOnaiaadIhadaWgaaWcbaGaaGimaa % qabaGccqGHsislcaaIXaGaaGOmaaGaay5bSlaawIa7aaqaamaakaaa % baWaaeWaaeaacaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaeyOeI0IaaG % OmaaGaayjkaiaawMcaamaaCaaaleqabaGaaGinaaaakiabgUcaRiaa % iMdaaSqabaaaaaaa!4ED2! \Leftrightarrow d\left( {I;\Delta } \right) = \frac{{\left| {6{x_0} - 12} \right|}}{{\sqrt {{{\left( {{x_0} - 2} \right)}^4} + 9} }}\)

Áp dụng BĐT: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaCa % aaleqabaGaaGOmaaaakiabgUcaRiaadkgadaahaaWcbeqaaiaaikda % aaGccqGHLjYScaaIYaGaamyyaiaadkgacaaMf8UaeyiaIiIaamyyai % aacYcacaWGIbaaaa!43B2! {a^2} + {b^2} \ge 2ab\quad \forall a,b\)

Tacó: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGyoaiabgU % caRmaabmaabaGaamiEamaaBaaaleaacaaIWaaabeaakiabgkHiTiaa % ikdaaiaawIcacaGLPaaadaahaaWcbeqaaiaaisdaaaGccqGHLjYSca % aIYaGaaiOlaiaaiodacaGGUaWaaeWaaeaacaWG4bWaaSbaaSqaaiaa % icdaaeqaaOGaeyOeI0IaaGOmaaGaayjkaiaawMcaamaaCaaaleqaba % GaaGOmaaaakiabgsDiBpaakaaabaGaaGyoaiabgUcaRmaabmaabaGa % amiEamaaBaaaleaacaaIWaaabeaakiabgkHiTiaaikdaaiaawIcaca % GLPaaadaahaaWcbeqaaiaaisdaaaaabeaakiabgwMiZoaakaaabaGa % aGOnamaabmaabaGaamiEamaaBaaaleaacaaIWaaabeaakiabgkHiTi % aaikdaaiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaaabeaaaaa!5B24! 9 + {\left( {{x_0} - 2} \right)^4} \ge 2.3.{\left( {{x_0} - 2} \right)^2} \Leftrightarrow \sqrt {9 + {{\left( {{x_0} - 2} \right)}^4}} \ge \sqrt {6{{\left( {{x_0} - 2} \right)}^2}} \)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % izamaabmaabaGaamysaiaacUdacqGHuoaraiaawIcacaGLPaaacqGH % 9aqpdaWcaaqaamaaemaabaGaaGOnaiaadIhadaWgaaWcbaGaaGimaa % qabaGccqGHsislcaaIXaGaaGOmaaGaay5bSlaawIa7aaqaamaakaaa % baWaaeWaaeaacaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaeyOeI0IaaG % OmaaGaayjkaiaawMcaamaaCaaaleqabaGaaGinaaaakiabgUcaRiaa % iMdaaSqabaaaaOGaeyizIm6aaSaaaeaadaabdaqaaiaaiAdacaWG4b % WaaSbaaSqaaiaaicdaaeqaaOGaeyOeI0IaaGymaiaaikdaaiaawEa7 % caGLiWoaaeaadaGcaaqaaiaaiAdadaqadaqaaiaadIhadaWgaaWcba % GaaGimaaqabaGccqGHsislcaaIYaaacaGLOaGaayzkaaWaaWbaaSqa % beaacaaIYaaaaaqabaaaaOGaeyypa0ZaaOaaaeaacaaI2aaaleqaaa % aa!6198! \Rightarrow d\left( {I;\Delta } \right) = \frac{{\left| {6{x_0} - 12} \right|}}{{\sqrt {{{\left( {{x_0} - 2} \right)}^4} + 9} }} \le \frac{{\left| {6{x_0} - 12} \right|}}{{\sqrt {6{{\left( {{x_0} - 2} \right)}^2}} }} = \sqrt 6 \)

Vậy giá trị lớn nhất mà  có thể đạt được là: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaOaaaeaaca % aI2aaaleqaaaaa!36CE! \sqrt 6\)

Phương trình tham số của đường thẳng d: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaeaafa % qabeWabaaabaGaamiEaiabg2da9iaaigdacqGHRaWkcaWG0baabaGa % amyEaiabg2da9iaaikdacqGHRaWkaeaacaWG6bGaeyypa0JaaGymai % abgUcaRiaaikdacaWG0baaaaGaay5EaaGaamiDaaaa!45A7! \left\{ {\begin{array}{*{20}{c}} {x = 1 + t}\\ {y = 2 + }\\ {z = 1 + 2t} \end{array}} \right.t\)\(( t\in R)\)

 \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamisaiabgI % GiolaadsgacqGHshI3caWGibWaaeWaaeaacaaIXaGaey4kaSIaamiD % aiaacUdacaaMc8UaaGOmaiabgUcaRiaadshacaGG7aGaaGPaVlaaig % dacqGHRaWkcaaIYaGaamiDaaGaayjkaiaawMcaaaaa!4AF3! H \in d \Rightarrow H\left( {1 + t;\,2 + t;\,1 + 2t} \right)\)

Độ dài \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiaadI % eacqGH9aqpdaGcaaqaamaabmaabaGaamiDaiabgkHiTiaaigdaaiaa % wIcacaGLPaaadaahaaWcbeqaaiaaikdaaaGccqGHRaWkdaqadaqaai % aadshacqGHRaWkcaaIXaaacaGLOaGaayzkaaWaaWbaaSqabeaacaaI % YaaaaOGaey4kaSYaaeWaaeaacaaIYaGaamiDaiabgkHiTiaaiodaai % aawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaaabeaakiabg2da9maa % kaaabaGaaGOnaiaadshadaahaaWcbeqaaiaaikdaaaGccqGHsislca % aIXaGaaGOmaiaadshacqGHRaWkcaaIXaGaaGymaaWcbeaakiabg2da % 9maakaaabaGaaGOnamaabmaabaGaamiDaiabgkHiTiaaigdaaiaawI % cacaGLPaaadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaaI1aaaleqa % aOGaeyyzIm7aaOaaaeaacaaI1aaaleqaaaaa!5F3F! AH = \sqrt {{{\left( {t - 1} \right)}^2} + {{\left( {t + 1} \right)}^2} + {{\left( {2t - 3} \right)}^2}} = \sqrt {6{t^2} - 12t + 11} = \sqrt {6{{\left( {t - 1} \right)}^2} + 5} \ge \sqrt 5 \)

Độ dài AH nhỏ nhất bằng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaOaaaeaaca % aI1aaaleqaaaaa!36CD! \sqrt 5 \) khi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDaiabg2 % da9iaaigdacqGHshI3caWGibWaaeWaaeaacaaIYaGaai4oaiaaioda % caGG7aGaaG4maaGaayjkaiaawMcaaaaa!4114! t = 1 \Rightarrow H\left( {2;3;3} \right)\).

Vậy a = 2;b = 3; c =3; \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % yyamaaCaaaleqabaGaaG4maaaakiabgUcaRiaadkgadaahaaWcbeqa % aiaaiodaaaGccqGHRaWkcaWGJbWaaWbaaSqabeaacaaIZaaaaOGaey % ypa0JaaGOnaiaaikdaaaa!4227! \Rightarrow {a^3} + {b^3} + {c^3} = 62\)

Ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY-Hhbbf9v8qqaqFr0xc9pk0xbb % a9q8WqFfeaY-biLkVcLq-JHqpepeea0-as0Fb9pgeaYRXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaaikdacaWG6b % WaaWbaaSqabeaacaaIYaaaaOGaeyOeI0IaaGOnaiaadQhacqGHRaWk % caaI1aGaeyypa0JaaGimaaaa!3EA3! 2{z^2} - 6z + 5 = 0\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY-Hhbbf9v8qqaqFr0xc9pk0xbb % a9q8WqFfeaY-biLkVcLq-JHqpepeea0-as0Fb9pgeaYRXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabgsDiBlaais % dacaWG6bWaaWbaaSqabeaacaaIYaaaaOGaeyOeI0IaaGymaiaaikda % caWG6bGaey4kaSIaaGymaiaaicdacqGH9aqpcaaIWaGaeyi1HS9aae % WaaeaacaaIYaGaamOEaiabgkHiTiaaiodaaiaawIcacaGLPaaadaah % aaWcbeqaaiaaikdaaaGccqGH9aqpcqGHsislcaaIXaGaeyypa0Jaam % yAamaaCaaaleqabaGaaGOmaaaakiabgsDiBlaadQhacqGH9aqpdaWc % aaqaaiaaiodacqGHXcqScaWGPbaabaGaaGOmaaaaaaa!5906! \Leftrightarrow 4{z^2} - 12z + 10 = 0 \Leftrightarrow {\left( {2z - 3} \right)^2} = - 1 = {i^2} \Leftrightarrow z = \frac{{3 \pm i}}{2}\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY-Hhbbf9v8qqaqFr0xc9pk0xbb % a9q8WqFfeaY-biLkVcLq-JHqpepeea0-as0Fb9pgeaYRXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabgkDiElaadQ % hadaWgaaWcbaGaaGimaaqabaGccqGH9aqpdaWcaaqaaiaaiodaaeaa % caaIYaaaaiabgkHiTmaalaaabaGaaGymaaqaaiaaikdaaaGaamyAai % abgkDiElaadMgacaWG6bWaaSbaaSqaaiaaicdaaeqaaOGaeyypa0Za % aSaaaeaacaaIXaaabaGaaGOmaaaacqGHRaWkdaWcaaqaaiaaiodaae % aacaaIYaaaaiaadMgaaaa!4B45! \Rightarrow {z_0} = \frac{3}{2} - \frac{1}{2}i \Rightarrow i{z_0} = \frac{1}{2} + \frac{3}{2}i\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdqKaai % OoaiaaykW7daWcaaqaaiaadIhacqGHsislcaaIYaaabaGaaGymaaaa % cqGH9aqpdaWcaaqaaiaadMhacqGHsislcaaIXaaabaGaaGymaaaacq % GH9aqpdaWcaaqaaiaadQhaaeaacqGHsislcaaIYaaaaaaa!4549! \Delta :\,\frac{{x - 2}}{1} = \frac{{y - 1}}{1} = \frac{z}{{ - 2}}\) đi qua M ( 2;1;0) và có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamODaiaads % hacaWGJbGaamiCaiaacQdacaaMc8UaaGPaVpaaFiaabaGaamyDaaGa % ay51GaGaeyypa0ZaaeWaaeaacaaIXaGaai4oaiaaykW7caaIXaGaai % 4oaiaaykW7cqGHsislcaaIYaaacaGLOaGaayzkaaaaaa!4A89! vtcp:\,\,\overrightarrow u = \left( {1;\,1;\, - 2} \right)\) .

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq % aHYoGyaiaawIcacaGLPaaacaGG6aGaaGPaVlaadIhacqGHRaWkcaWG % 5bGaey4kaSIaaGOmaiaadQhacqGHRaWkcaaIXaGaeyypa0JaaGimaa % aa!443E! \left( \beta \right):\,x + y + 2z + 1 = 0\) có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamODaiaads % hacaWGWbGaamiDaiaacQdacaaMc8UaaGPaVpaaFiaabaGaamOBaaGa % ay51GaGaeyypa0ZaaeWaaeaacaaIXaGaai4oaiaaykW7caaIXaGaai % 4oaiaaykW7caaIYaaacaGLOaGaayzkaaaaaa!49A6! vtpt:\,\,\overrightarrow n = \left( {1;\,1;\,2} \right)\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq % aHXoqyaiaawIcacaGLPaaacaGG6aGaaGPaVpaaceaaeaqabeaaqaaa % aaaaaaWdbiaadgracaWGPbGaaeiiaiaadghacaWG1bGaamyyaiaayk % W7caWGnbaabaGaamODaiaadshacaWGWbGaamiDaiaaykW7daWadaqa % amaaFiaabaGaamyDaaGaay51GaGaaiilaiaaykW7daWhcaqaaiaad6 % gaaiaawEniaaGaay5waiaaw2faaiabg2da9maabmaabaGaaGinaiaa % cUdacaaMc8UaeyOeI0IaaGinaiaacUdacaaMc8UaaGimaaGaayjkai % aawMcaaiabg2da9iaaisdadaqadaqaaiaaigdacaGG7aGaaGPaVlab % gkHiTiaaigdacaGG7aGaaGPaVlaaicdaaiaawIcacaGLPaaaaaWdai % aawUhaaaaa!6843! \left( \alpha \right):\,\left\{ \begin{array}{l} đi{\rm{ }}qua\,M\\ vtpt\,\left[ {\overrightarrow u ,\,\overrightarrow n } \right] = \left( {4;\, - 4;\,0} \right) = 4\left( {1;\, - 1;\,0} \right) \end{array} \right.\)

Phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq % aHXoqyaiaawIcacaGLPaaacaGG6aGaaGPaVpaabmaabaGaamiEaiab % gkHiTiaaikdaaiaawIcacaGLPaaacqGHsisldaqadaqaaiaadMhacq % GHsislcaaIXaaacaGLOaGaayzkaaGaeyypa0JaaGimaaaa!4670! \left( \alpha \right):\,\left( {x - 2} \right) - \left( {y - 1} \right) = 0\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % iEaiabgkHiTiaadMhacqGHsislcaaIXaGaeyypa0JaaGimaaaa!3EA0! \Leftrightarrow x - y - 1 = 0\)

Gọi (d) là giao tuyến của hai mặt phẳng \((\alpha)\),\((\beta)\) . 

ta có (d) đi qua N(0 ; -1 ; 0) ;

(d) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 % qacaWG2bGaamiDaiaadogacaWGWbWdaiaayEW7peWaamWaa8aabaWd % biqad6gagaWcaiaacYcapaGaaG5bV-qadaWhcaWdaeaapeGaamOBa8 % aadaWgaaWcbaWdbiabeg7aHbWdaeqaaaGcpeGaay51GaaacaGLBbGa % ayzxaaGaeyypa0ZaaeWaa8aabaWdbiaaikdacaGG7aWdaiaayEW7pe % GaaGOmaiaacUdapaGaaG5bV-qacqGHsislcaaIYaaacaGLOaGaayzk % aaGaeyypa0JaaGOmamaabmaapaqaa8qacaaIXaGaai4oa8aacaaMh8 % +dbiaaigdacaGG7aWdaiaayEW7peGaeyOeI0IaaGymaaGaayjkaiaa % wMcaaaaa!5BF1! vtcp{\mkern 1mu} \left[ {\vec n,{\mkern 1mu} \overrightarrow {{n_\alpha }} } \right] = \left( {2;{\mkern 1mu} 2;{\mkern 1mu} - 2} \right) = 2\left( {1;{\mkern 1mu} 1;{\mkern 1mu} - 1} \right)\)

Phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WGKbaacaGLOaGaayzkaaGaaiOoaiaaykW7caaMc8+aaSaaaeaacaWG % 4baabaGaaGymaaaacqGH9aqpdaWcaaqaaiaadMhacqGHRaWkcaaIXa % aabaGaaGymaaaacqGH9aqpdaWcaaqaaiaadQhaaeaacqGHsislcaaI % Xaaaaaaa!462B! \left( d \right):\,\,\frac{x}{1} = \frac{{y + 1}}{1} = \frac{z}{{ - 1}}\)

Giá trị nhỏ nhất của hàm số \(y = \frac{{x - 1}}{{2 - x}}\)trên đoạn [3;4] là -2 

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qaaeaada % qadaqaaiaaikdacaWG4bGaey4kaSIaaGymaaGaayjkaiaawMcaaaWc % beqab0Gaey4kIipakiaabsgacaWG4bGaeyypa0JaamiEamaaCaaale % qabaGaaGOmaaaakiabgUcaRiaadIhacqGHRaWkcaWGdbaaaa!453B! \int {\left( {2x + 1} \right)} {\rm{d}}x = {x^2} + x + C\)

Ta có  \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiaacE % cacqGH9aqpdaWadaqaaiaadAgadaqadaqaaiaadIhadaahaaWcbeqa % aiaaikdaaaaakiaawIcacaGLPaaaaiaawUfacaGLDbaadaahaaWcbe % qaaiaac+caaaGccqGH9aqpcaaIYaGaamiEaiaac6cacaWGMbGaai4j % amaabmaabaGaamiEamaaCaaaleqabaGaaGOmaaaaaOGaayjkaiaawM % caaaaa!4863! y' = {\left[ {f\left( {{x^2}} \right)} \right]^/} = 2x.f'\left( {{x^2}} \right)\)

Hàm số nghịch biến

\( \Leftrightarrow y' < 0 \Leftrightarrow \left[ \begin{array}{l} \left\{ \begin{array}{l} x > 0\\ f'\left( {{x^2}} \right) < 0 \end{array} \right.\\ \left\{ \begin{array}{l} x < 0\\ f'\left( {{x^2}} \right) > 0 \end{array} \right. \end{array} \right.\left[ \begin{array}{l} \left\{ \begin{array}{l} x > 0\\ {x^2} < - 1 \vee 1 < {x^2} < 4 \end{array} \right.\\ \left\{ \begin{array}{l} x < 0\\ - 1 < {x^2} < 1 \vee {x^2} > 4 \end{array} \right. \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} 1 < x < 2\\ x < - 2 \vee - 1 < x < 0 \end{array} \right.\)

Vậy hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadAgadaqadaqaaiaadIhadaahaaWcbeqaaiaaikdaaaaakiaa % wIcacaGLPaaaaaa!3C5C! y = f\left( {{x^2}} \right)\) có 3 khoảng nghịch biến

Trong khai triển nhị thức \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WGHbGaey4kaSIaamOyaaGaayjkaiaawMcaamaaCaaaleqabaGaamOB % aaaaaaa!3B4C! {\left( {a + b} \right)^n}\) thì số các số hạng là n + 1 nên trong khai triển \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % aIYaGaamiEaiabgkHiTiaaiodaaiaawIcacaGLPaaadaahaaWcbeqa % aiaaikdacaaIWaGaaGymaiaaiIdaaaaaaa!3E00! {\left( {2x - 3} \right)^{2018}}\) có 2019 số hạng

Có vô số mặt cầu chứa được một đường tròn cho trước

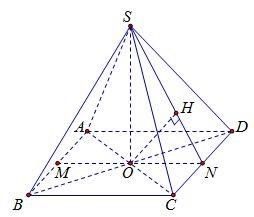
Gọi M,N lần lượt là trung điểm của các cạnh AB; CDCD; H là hình chiếu vuông góc của O trên SN

Vì AB// CD nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizamaabm % aabaGaamyqaiaadkeacaGGSaGaai4uaiaacoeaaiaawIcacaGLPaaa % cqGH9aqpcaWGKbWaaeWaaeaacaWGbbGaamOqaiaacYcacaGGOaGaam % 4uaiaadoeacaWGebGaaiykaaGaayjkaiaawMcaaiabg2da9iaadsga % daqadaqaaiaad2eacaGGSaGaaiikaiaadofacaWGdbGaamiraiaacM % caaiaawIcacaGLPaaacqGH9aqpcaaIYaGaamizamaabmaabaGaam4t % aiaacYcacaGGOaGaam4uaiaadoeacaWGebGaaiykaaGaayjkaiaawM % caaaaa!57EE! d\left( {AB,SC} \right) = d\left( {AB,(SCD)} \right) = d\left( {M,(SCD)} \right) = 2d\left( {O,(SCD)} \right)\)

Ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaqaabe % qaaiaadoeacaWGebGaeyyPI4Laam4uaiaad+eaaeaacaWGdbGaamir % aiabgwQiEjaad+eacaWGobaaaiaawUhaaiabgkDiElaadoeacaWGeb % GaeyyPI4LaaiikaiaadofacaWGpbGaamOtaiaacMcacqGHshI3caWG % dbGaamiraiabgwQiEjaad+eacaWGibaaaa!51A2! \left\{ \begin{array}{l} CD \bot SO\\ CD \bot ON \end{array} \right. \Rightarrow CD \bot (SON) \Rightarrow CD \bot OH\)

Khi đó \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaqaabe % qaaiaadoeacaWGebGaeyyPI4Laam4taiaadIeaaeaacaWGpbGaamis % aiabgwQiEjaadofacaWGobaaaiaawUhaaiabgkDiElaad+eacaWGib % GaeyyPI4LaaiikaiaadofacaWGdbGaamiraiaacMcacqGHshI3caWG % KbWaaeWaaeaacaWGpbGaai4oaiaacIcacaWGtbGaam4qaiaadseaca % GGPaaacaGLOaGaayzkaaGaeyypa0Jaam4taiaadIeacaGGUaaaaa!57E2! \left\{ \begin{array}{l} CD \bot OH\\ OH \bot SN \end{array} \right. \Rightarrow OH \bot (SCD) \Rightarrow d\left( {O;(SCD)} \right) = OH.\)

Tam giác SON vuông tại O nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaam4taiaadIeadaahaaWcbeqaaiaaikdaaaaaaOGaeyyp % a0ZaaSaaaeaacaaIXaaabaGaam4taiaad6eadaahaaWcbeqaaiaaik % daaaaaaOGaey4kaSYaaSaaaeaacaaIXaaabaGaam4taiaadofadaah % aaWcbeqaaiaaikdaaaaaaOGaeyypa0ZaaSaaaeaacaaIXaaabaWaaS % aaaeaacaWGHbWaaWbaaSqabeaacaaIYaaaaaGcbaGaaGinaaaaaaGa % ey4kaSYaaSaaaeaacaaIXaaabaGaamyyamaaCaaaleqabaGaaGOmaa % aaaaGccqGH9aqpdaWcaaqaaiaaiwdaaeaacaWGHbWaaWbaaSqabeaa % caaIYaaaaaaakiabgkDiElaad+eacaWGibGaeyypa0ZaaSaaaeaaca % WGHbaabaWaaOaaaeaacaaI1aaaleqaaaaaaaa!5489! \frac{1}{{O{H^2}}} = \frac{1}{{O{N^2}}} + \frac{1}{{O{S^2}}} = \frac{1}{{\frac{{{a^2}}}{4}}} + \frac{1}{{{a^2}}} = \frac{5}{{{a^2}}} \Rightarrow OH = \frac{a}{{\sqrt 5 }}\)

Vậy \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizamaabm % aabaGaamyqaiaadkeacaGGSaGaai4uaiaacoeaaiaawIcacaGLPaaa % cqGH9aqpcaaIYaGaam4taiaadIeacqGH9aqpdaWcaaqaaiaaikdaca % WGHbWaaOaaaeaacaaI1aaaleqaaaGcbaGaaGynaaaaaaa!43FF! d\left( {AB,SC} \right) = 2OH = \frac{{2a\sqrt 5 }}{5}\)

Phương trình hoành độ giao điểm của đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Lq-Jirpepeea0-as0Fb9pgea0lXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMhacqGH9a % qpdaWcaaqaaiaadIhacqGHRaWkcaaIXaaabaGaamiEaiabgkHiTiaa % ikdaaaaaaa!3DBB! y = \frac{{x + 1}}{{x - 2}}\) và trục hoành: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Lq-Jirpepeea0-as0Fb9pgea0lXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaalaaabaGaam % iEaiabgUcaRiaaigdaaeaacaWG4bGaeyOeI0IaaGOmaaaacqGH9aqp % caaIWaGaaGPaVpaabmaabaGaamiEaabaaaaaaaaapeGafyypa0JbaO % aacaaIYaaapaGaayjkaiaawMcaaaaa!438A! \frac{{x + 1}}{{x - 2}} = 0\,\left( {x\not = 2} \right)\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Lq-Jirpepeea0-as0Fb9pgea0lXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabgsDiBlaadI % hacqGH9aqpcqGHsislcaaIXaaaaa!3C6E! \Leftrightarrow x = - 1\)

Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Lq-Jirpepeea0-as0Fb9pgea0lXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMhacqGH9a % qpdaWcaaqaaiaadIhacqGHRaWkcaaIXaaabaGaamiEaiabgkHiTiaa % ikdaaaaaaa!3DBB! y = \frac{{x + 1}}{{x - 2}}\) và các trục tọa độ bằng:

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0Firpepeuj0xe9Fve9 % Fve9qapdbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaada % abdaqaamaalaaabaGaamiEaiabgUcaRiaaigdaaeaacaWG4bGaeyOe % I0IaaGOmaaaaaiaawEa7caGLiWoaaSqaaiabgkHiTiaaigdaaeaaca % aIWaaaniabgUIiYdGccaqGKbGaamiEaaaa!46F5! \int\limits_{ - 1}^0 {\left| {\frac{{x + 1}}{{x - 2}}} \right|} {\rm{d}}x\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0Firpepeuj0xe9Fve9 % Fve9qapdbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Zaaq % WaaeaadaWdXbqaamaalaaabaGaamiEaiabgUcaRiaaigdaaeaacaWG % 4bGaeyOeI0IaaGOmaaaaaSqaaiabgkHiTiaaigdaaeaacaaIWaaani % abgUIiYdGccaqGKbGaamiEaaGaay5bSlaawIa7aaaa!47FB! = \left| {\int\limits_{ - 1}^0 {\frac{{x + 1}}{{x - 2}}} {\rm{d}}x} \right|\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0Firpepeuj0xe9Fve9 % Fve9qapdbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Zaaq % WaaeaadaWdXbqaamaabmaabaGaaGymaiabgUcaRmaalaaabaGaaG4m % aaqaaiaadIhacqGHsislcaaIYaaaaaGaayjkaiaawMcaaaWcbaGaey % OeI0IaaGymaaqaaiaaicdaa0Gaey4kIipakiaabsgacaWG4baacaGL % hWUaayjcSdaaaa!4944! = \left| {\int\limits_{ - 1}^0 {\left( {1 + \frac{3}{{x - 2}}} \right)} {\rm{d}}x} \right|\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0Firpepeuj0xe9Fve9 % Fve9qapdbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Zaaq % WaaeaadaabcaqaamaabmaabaGaamiEaiabgUcaRiaaiodaciGGSbGa % aiOBamaaemaabaGaamiEaiabgkHiTiaaikdaaiaawEa7caGLiWoaai % aawIcacaGLPaaaaiaawIa7amaaDaaaleaacqGHsislcaaIXaaabaGa % aGimaaaaaOGaay5bSlaawIa7aaaa!4BF2! = \left| {\left. {\left( {x + 3\ln \left| {x - 2} \right|} \right)} \right|_{ - 1}^0} \right|\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0Firpepeuj0xe9Fve9 % Fve9qapdbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Zaaq % WaaeaacaaIXaGaey4kaSIaaG4maiGacYgacaGGUbWaaSaaaeaacaaI % YaaabaGaaG4maaaaaiaawEa7caGLiWoaaaa!41B9! = \left| {1 + 3\ln \frac{2}{3}} \right|\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0Firpepeuj0xe9Fve9 % Fve9qapdbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Jaey % OeI0IaaGymaiabgkHiTiaaiodaciGGSbGaaiOBamaalaaabaGaaGOm % aaqaaiaaiodaaaaaaa!3F8F! = - 1 - 3\ln \frac{2}{3}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0Firpepeuj0xe9Fve9 % Fve9qapdbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0JaaG % 4maiGacYgacaGGUbWaaSaaaeaacaaIZaaabaGaaGOmaaaacqGHsisl % caaIXaaaaa!3EA2! = 3\ln \frac{3}{2} - 1\)

Gọi chiều cao hình nón là h, bán kính đáy bằng a, ta có:

Độ dài đường sinh \( l = \sqrt {{{(a\sqrt 3 )}^2} + {a^2}} = 2a\)

Do đó: \(S_xq= \pi.r.l=2\pi.a^2\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOEaiabg2 % da9iaadQhadaWgaaWcbaGaaGymaaqabaGccqGHRaWkcaWG6bWaaSba % aSqaaiaaikdaaeqaaOGaeyypa0JaaGOmaiabgUcaRiaaiodacaWGPb % GaeyOeI0IaaGinaiabgkHiTiaaiwdacaWGPbGaeyypa0JaeyOeI0Ia % aGOmaiabgkHiTiaaikdacaWGPbaaaa!4A96! z = {z_1} + {z_2} = 2 + 3i - 4 - 5i = - 2 - 2i\)

Kẻ \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4taiaadI % eacqGHLkIxcaWGbbGaamysaaaa!3ADA! OH \bot AI\) . Nhận xét OM // (ABN) nên khoảng cách h giữa hai đường thẳng AB và OM bằng khoảng cách giữa đường thẳng OM và mặt phẳng (ABN), bằng khoảng cách từ O đến mặt phẳng (ABN) . Suy ra \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiAaiabg2 % da9iaadsgadaqadaqaaiaad+eacaGGSaWaaeWaaeaacaWGbbGaamOq % aiaad6eaaiaawIcacaGLPaaaaiaawIcacaGLPaaacqGH9aqpcaWGpb % Gaamisaaaa!426D! h = d\left( {O,\left( {ABN} \right)} \right) = OH\)

Tam giác OBI có OB = a, \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaecaaeaaca % WGcbGaam4taiaad2eaaiaawkWaaiabg2da9iaaiAdacaaIWaWaaWba % aSqabeaacaqGVbaaaaaa!3CC2! \widehat {BOM} = {60^{\rm{o}}}\) nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4taiaadM % eacqGH9aqpdaWcaaqaaiaadggadaGcaaqaaiaaiodaaSqabaaakeaa % caaIYaaaaaaa!3B30! OI = \frac{{a\sqrt 3 }}{2}\).

Tam giác AOI vuông tại O nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaam4taiaadIeadaahaaWcbeqaaiaaikdaaaaaaOGaeyyp % a0ZaaSaaaeaacaaIXaaabaGaam4taiaadgeadaahaaWcbeqaaiaaik % daaaaaaOGaey4kaSYaaSaaaeaacaaIXaaabaGaam4taiaadMeadaah % aaWcbeqaaiaaikdaaaaaaaaa!41E9! \frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{I^2}}}\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aaS % aaaeaacaaIXaaabaGaam4taiaadIeadaahaaWcbeqaaiaaikdaaaaa % aOGaeyypa0ZaaSaaaeaacaaIXaaabaGaaG4maiaadggadaahaaWcbe % qaaiaaikdaaaaaaOGaey4kaSYaaSaaaeaacaaI0aaabaGaaG4maiaa % dggadaahaaWcbeqaaiaaikdaaaaaaaaa!4452! \Leftrightarrow \frac{1}{{O{H^2}}} = \frac{1}{{3{a^2}}} + \frac{4}{{3{a^2}}}\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % 4taiaadIeacqGH9aqpdaWcaaqaaiaadggadaGcaaqaaiaaiodaaSqa % baaakeaadaGcaaqaaiaaiwdaaSqabaaaaaaa!3DAA! \Rightarrow OH = \frac{{a\sqrt 3 }}{{\sqrt 5 }}\)

Xét: \(ac(b^2-4ac) > 0\)  hay ac > 0 ; \(b^2 - 4ac > 0\)

Xét phương trình hoành độ giao điểm: \(ax^4+bx^2+c = 0\).

Đặt \(x^2 = t ( t \geq0)\).Phương trình theo  t:  .\(at^2+bt+c = 0\)

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaeaafa % qabeWabaaaeaqabeaacqqHuoarcqGH9aqpcaWGIbWaaWbaaSqabeaa % caaIYaaaaOGaeyOeI0IaaGinaiaadggacaWGJbaabaGaamiDaiabgU % caRiaadshaaaqaaaqaaaaaaiaawUhaaaaa!41B7! \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \Delta = {b^2} - 4ac> 0\\ t_1+t_2 = \frac{-b}{a} >0 \end{array}\\ {t_1.t_2= \frac{c}{a}> 0}\\ \end{array}} \right.\) Phương trình hai nghiệm dương phân biệt.

Suy ra \(ax^4+bx^2+c=0\) có bốn nghiệm phân biệt. Vậy đồ thị hàm số cắt trục hoành tại bốn điểm phân biệt.

Phương trình hoành độ giao điểm của đồ thị \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaikdaaaGccqGHsislcaaIYaGaamiE % aaaa!3C8E! y = {x^2} - 2x\) và y = 0 là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCa % aaleqabaGaaGOmaaaakiabgkHiTiaaikdacaWG4bGaeyypa0JaaGim % aaaa!3C4A! {x^2} - 2x = 0\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aam % qaaqaabeqaaiaadIhacqGH9aqpcaaIWaaabaGaamiEaiabg2da9iaa % ikdaaaGaay5waaaaaa!3ECE! \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 2 \end{array} \right.\)

Trên đoạn [-10 ; 10] ta có

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCa % aaleqabaGaaGOmaaaakiabgkHiTiaaikdacaWG4bGaeyyzImRaaGim % aaaa!3D0A! {x^2} - 2x \ge 0\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyiaIiIaam % iEaiabgIGiopaadmaabaGaeyOeI0IaaGymaiaaicdacaGG7aGaaGim % aaGaay5waiaaw2faaaaa!3F12! \forall x \in \left[ { - 10;0} \right]\) và [2;10].

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCa % aaleqabaGaaGOmaaaakiabgkHiTiaaikdacaWG4bGaeyizImQaaGim % aaaa!3CF9! {x^2} - 2x \le 0\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyiaIiIaam % iEaiabgIGiopaadmaabaGaaGimaiaacUdacaaIYaaacaGLBbGaayzx % aaaaaa!3D6C! ;\forall x \in \left[ {0;2} \right]\)

Do đó  \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiabg2 % da9maapehabiqaaqObdaabdaqaaiaadIhadaahaaWcbeqaaiaaikda % aaGccqGHsislcaaIYaGaamiEaaGaay5bSlaawIa7aiaabsgacaWG4b % aaleaacqGHsislcaaIXaGaaGimaaqaaiaaigdacaaIWaaaniabgUIi % Ydaaaa!483A! S = \int\limits_{ - 10}^{10} {\left| {{x^2} - 2x} \right|{\rm{d}}x} \)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Zaa8 % qCaeGabaaHgmaabmaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiab % gkHiTiaaikdacaWG4baacaGLOaGaayzkaaGaaeizaiaadIhaaSqaai % abgkHiTiaaigdacaaIWaaabaGaaGimaaqdcqGHRiI8aOGaeyOeI0Ya % a8qCaeGabaaHgmaabmaabaGaamiEamaaCaaaleqabaGaaGOmaaaaki % abgkHiTiaaikdacaWG4baacaGLOaGaayzkaaGaaeizaiaadIhaaSqa % aiaaicdaaeaacaaIYaaaniabgUIiYdGccqGHRaWkdaWdXbqaceaaeA % WaaeWaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaeyOeI0IaaGOm % aiaadIhaaiaawIcacaGLPaaacaqGKbGaamiEaaWcbaGaaGOmaaqaai % aaigdacaaIWaaaniabgUIiYdaaaa!608A! = \int\limits_{ - 10}^0 {\left( {{x^2} - 2x} \right){\rm{d}}x} - \int\limits_0^2 {\left( {{x^2} - 2x} \right){\rm{d}}x} + \int\limits_2^{10} {\left( {{x^2} - 2x} \right){\rm{d}}x} \)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS % aaaeaacaaIYaGaaGimaiaaicdacaaI4aaabaGaaG4maaaaaaa!3AB9! = \frac{{2008}}{3}\)

Gọi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOEaiabg2 % da9iaadIhacqGHRaWkcaWG5bGaamyAaaaa!3BC4! z = x + yi\), \(x,y \in R\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % ytamaabmaabaGaamiEaiaacUdacaWG5baacaGLOaGaayzkaaaaaa!3D66! \Rightarrow M\left( {x;y} \right)\)

N là điểm đối xứng của M qua Oy \(\Rightarrow N( -x;y) \)

\(\Rightarrow w = -x + yi = -(x-yi) = - \bar{z} \)

Ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafa % Gaeyypa0ZaaSaaaeaacaaIYaGaamiEaiabgUcaRiaad2gaaeaacaWG % 4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaamyBaiaadIhacqGHRa % WkcaaIXaaaaiabgwMiZkaaicdaaaa!447F! y' = \frac{{2x + m}}{{{x^2} + mx + 1}} \ge 0\) với mọi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabgI % GiopaabmaabaGaaGimaiaacUdacqGHRaWkcqGHEisPaiaawIcacaGL % PaaacaGGUaaaaa!3E7C! x \in \left( {0; + \infty } \right).\)

Xét \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4zamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9iaadIhadaahaaWcbeqa % aiaaikdaaaGccqGHRaWkcaWGTbGaamiEaiabgUcaRiaaigdaaaa!40CA! g\left( x \right) = {x^2} + mx + 1\) có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdqKaey % ypa0JaamyBamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaisdacaGG % Uaaaaa!3CA2! \Delta = {m^2} - 4.\)

TH1: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdqKaey % ipaWJaaGimaiabgsDiBlabgkHiTiaaikdacqGH8aapcaWGTbGaeyip % aWJaaGOmaaaa!40D3! \Delta < 0 \Leftrightarrow - 2 < m < 2\) khi đó \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4zamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg6da+iaaicdacaGGSaGaeyia % IiIaamiEaiabgIGiolabl2riHcaa!4099! g\left( x \right) > 0,\forall x \in R\) nên ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOmaiaadI % hacqGHRaWkcaWGTbGaeyyzImRaaGimaaaa!3C01! 2x + m \ge 0\),\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyiaIiIaam % iEaiabgIGiopaabmaabaGaaGimaiaacUdacqGHRaWkcqGHEisPaiaa % wIcacaGLPaaaaaa!3E9A! \forall x \in \left( {0; + \infty } \right)\)

Suy ra \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGimaiabgs % MiJkaad2gacqGH8aapcaaIYaaaaa!3B15! 0 \le m < 2\).

TH2: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdqKaey % yzImRaaGimaiabgsDiBpaadeaaeaqabeaacaWGTbGaeyizImQaeyOe % I0IaaGOmaaqaaiaad2gacqGHLjYScaaIYaaaaiaawUfaaiaac6caaa % a!45AE! \Delta \ge 0 \Leftrightarrow \left[ \begin{array}{l} m \le - 2\\ m \ge 2 \end{array} \right..\)

Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBaiabgs % MiJkabgkHiTiaaikdaaaa!3A44! m \le - 2\) thì \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcaaIWaaabeaakiqa % dMhagaqbaiabg2da9iaad2gacqGHKjYOcqGHsislcaaIYaaaaa!430B! \mathop {\lim }\limits_{x \to 0} y' = m \le - 2\) nên không thỏa \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafa % Gaeyypa0ZaaSaaaeaacaaIYaGaamiEaiabgUcaRiaad2gaaeaacaWG % 4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaamyBaiaadIhacqGHRa % WkcaaIXaaaaiabgwMiZkaaicdaaaa!447F! y' = \frac{{2x + m}}{{{x^2} + mx + 1}} \ge 0\) với mọi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabgI % GiopaabmaabaGaaGimaiaacUdacqGHRaWkcqGHEisPaiaawIcacaGL % PaaacaGGUaaaaa!3E7C! x \in \left( {0; + \infty } \right).\)

Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBaiabgw % MiZkaaikdaaaa!3968! m \ge 2\) thì \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOmaiaadI % hacqGHRaWkcaWGTbGaeyOpa4JaaGimaaaa!3B43! 2x + m > 0\) với mọi \(x\in (0; + \infty)\) và g(x) có 2 nghiệm âm . Do đó g(x) > 0 ,\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyiaIiIaam % iEaiabgIGiopaabmaabaGaaGimaiaacUdacqGHRaWkcqGHEisPaiaa % wIcacaGLPaaaaaa!3E9A! \forall x \in \left( {0; + \infty } \right)\) . Suy ra \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOmaiabgs % MiJkaad2gacqGH8aapcaaIXaGaaGimaaaa!3BD0! 2 \le m < 10\).

Vậy ta có:\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGimaiabgs % MiJkaad2gacqGH8aapcaaIXaGaaGimaaaa!3BCE! 0 \le m < 10\)  nên có 10 giá trị nguyên của m.

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafa % Gaeyypa0JaaG4maiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHsisl % caaI2aGaamiEaiabgUcaRiaaiodacaWGTbaaaa!3FEC! y' = 3{x^2} - 6x + 3m\); \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafa % Gaeyypa0JaaGimaiabgsDiBlaadIhadaahaaWcbeqaaiaaikdaaaGc % cqGHsislcaaIYaGaamiEaiabgUcaRiaad2gacqGH9aqpcaaIWaaaaa!4344! y' = 0 \Leftrightarrow {x^2} - 2x + m = 0\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGafuiLdqKbau % aacqGH9aqpcaaIXaGaeyOeI0IaamyBaaaa!3B06! \Delta ' = 1 - m\)

hàm số có hai điểm cực trị \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTafu % iLdqKbauaacqGH+aGpcaaIWaaaaa!3B84! \Leftrightarrow \Delta ' > 0\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % yBaiabgYda8iaaigdaaaa!3B01! \Leftrightarrow m < 1\)(1). Mặt khác \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafy % aafaGaeyypa0JaaGOnaiaadIhacqGHsislcaaI2aaaaa!3B79! y'' = 6x - 6\) .

 \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafy % aafaGaeyypa0JaaGimaaaa!38C9! y'' = 0\)\(\iff x = 1 \Rightarrow y = 4m - 3\)

Hàm số bậc ba có đồ thị nhận điểm uốn làm tâm đối xứng. Do đó:

m cần tìm thoả (1) và điểm uốn nằm trên trục hoành

 m < 1 và  4m - 3 = 0 \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % yBaiabg2da9maalaaabaGaaG4maaqaaiaaisdaaaaaaa!3BD3! \Leftrightarrow m = \frac{3}{4}\)

Gọi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysamaabm % aabaGaeyOeI0IaaGymaiabgkHiTiaadshacaGG7aGaeyOeI0IaamiD % aiaacUdacaaIYaGaey4kaSIaamiDaaGaayjkaiaawMcaaiabgIGiol % aadsgacaGGUaWaa8HaaeaacaWGjbGaamyqaaGaay51GaGaeyypa0Za % aeWaaeaacaWG0bGaai4oaiaadshacqGHRaWkcaaIYaGaai4oaiabgk % HiTiaadshacqGHsislcaaIXaaacaGLOaGaayzkaaGaaiilamaaFiaa % baGaamysaiaadkeaaiaawEniaiabg2da9maabmaabaGaamiDaiabgU % caRiaaiodacaGG7aGaamiDaiabgUcaRiaaiodacaGG7aGaeyOeI0Ia % amiDaaGaayjkaiaawMcaaaaa!6281! I\left( { - 1 - t; - t;2 + t} \right) \in d.\overrightarrow {IA} = \left( {t;t + 2; - t - 1} \right),\overrightarrow {IB} = \left( {t + 3;t + 3; - t} \right)\)

Do ABCD là hình thoi nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8Haaeaaca % WGjbGaamyqaaGaay51GaGaaiOlamaaFiaabaGaamysaiaadkeaaiaa % wEniaiabg2da9iaaicdacqGHuhY2caaIZaGaamiDamaaCaaaleqaba % GaaGOmaaaakiabgUcaRiaaiMdacaWG0bGaey4kaSIaaGOnaiabg2da % 9iaaicdacqGHuhY2caWG0bGaeyypa0JaeyOeI0IaaGOmaiaacUdaca % WG0bGaeyypa0JaeyOeI0IaaGymaaaa!5465! \overrightarrow {IA} .\overrightarrow {IB} = 0 \Leftrightarrow 3{t^2} + 9t + 6 = 0 \Leftrightarrow t = - 2;t = - 1\).

Do C đối xứng A qua I và D đối xứng B qua I nên:

+) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDaiabg2 % da9iabgkHiTiaaigdacqGHshI3caWGjbWaaeWaaeaacaaIWaGaai4o % aiaaigdacaGG7aGaaGymaaGaayjkaiaawMcaaiabgkDiElaadoeada % qadaqaaiaaigdacaGG7aGaaGimaiaacUdacaaIXaaacaGLOaGaayzk % aaGaaiilaiaadseadaqadaqaaiabgkHiTiaaikdacaGG7aGaeyOeI0 % IaaGymaiaacUdacaaIWaaacaGLOaGaayzkaaaaaa!52E3! t = - 1 \Rightarrow I\left( {0;1;1} \right) \Rightarrow C\left( {1;0;1} \right),D\left( { - 2; - 1;0} \right)\)

+) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDaiabg2 % da9iabgkHiTiaaikdacqGHshI3caWGdbWaaeWaaeaacaaIZaGaai4o % aiaaikdacaGG7aGaeyOeI0IaaGymaaGaayjkaiaawMcaaiaacYcaca % WGebWaaeWaaeaacaaIWaGaai4oaiaaigdacaGG7aGaeyOeI0IaaGOm % aaGaayjkaiaawMcaaaaa!4A86! t = - 2 \Rightarrow C\left( {3;2; - 1} \right),D\left( {0;1; - 2} \right)\)

Nhìn vào đồ thị ta thấy hàm số y = f(x) đồng biến trên khoảng (0;2).

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Lq-Jirpepeea0-as0Fb9pgea0lXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaapedabaWaam % WaaeaacaWGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaey4kaSIa % aG4maiaadEgadaqadaqaaiaadIhaaiaawIcacaGLPaaaaiaawUfaca % GLDbaacaqGKbGaamiEaaWcbaGaaGymaaqaaiaaiodaa0Gaey4kIipa % kiabg2da9iaaigdacaaIWaaaaa!48E5! \int_1^3 {\left[ {f\left( x \right) + 3g\left( x \right)} \right]{\rm{d}}x} = 10\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Lq-Jirpepeea0-as0Fb9pgea0lXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabgsDiBpaape % dabaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiaabsgacaWG % 4baaleaacaaIXaaabaGaaG4maaqdcqGHRiI8aOGaey4kaSIaaG4mam % aapedabaGaam4zamaabmaabaGaamiEaaGaayjkaiaawMcaaiaabsga % caWG4baaleaacaaIXaaabaGaaG4maaqdcqGHRiI8aOGaeyypa0JaaG % ymaiaaicdadaqadaqaaiaaigdaaiaawIcacaGLPaaaaaa!5122! \Leftrightarrow \int_1^3 {f\left( x \right){\rm{d}}x} + 3\int_1^3 {g\left( x \right){\rm{d}}x} = 10\left( 1 \right)\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Lq-Jirpepeea0-as0Fb9pgea0lXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaapedabaWaam % WaaeaacaaIYaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiab % gkHiTiaadEgadaqadaqaaiaadIhaaiaawIcacaGLPaaaaiaawUfaca % GLDbaacaqGKbGaamiEaaWcbaGaaGymaaqaaiaaiodaa0Gaey4kIipa % kiabg2da9iaaiAdaaaa!4839! \int_1^3 {\left[ {2f\left( x \right) - g\left( x \right)} \right]{\rm{d}}x} = 6\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Lq-Jirpepeea0-as0Fb9pgea0lXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabgsDiBlaaik % dadaWdXaqaaiaadAgadaqadaqaaiaadIhaaiaawIcacaGLPaaacaqG % KbGaamiEaaWcbaGaaGymaaqaaiaaiodaa0Gaey4kIipakiabgkHiTm % aapedabaGaam4zamaabmaabaGaamiEaaGaayjkaiaawMcaaiaabsga % caWG4baaleaacaaIXaaabaGaaG4maaqdcqGHRiI8aOGaeyypa0JaaG % OnaiaaykW7daqadaqaaiaaikdaaiaawIcacaGLPaaaaaa!5202! \Leftrightarrow 2\int_1^3 {f\left( x \right){\rm{d}}x} - \int_1^3 {g\left( x \right){\rm{d}}x} = 6\,\left( 2 \right)\)

Giải hệ (1) ; (2) ta được \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Lq-Jirpepeea0-as0Fb9pgea0lXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabgsDiBpaape % dabaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiaabsgacaWG % 4baaleaacaaIXaaabaGaaG4maaqdcqGHRiI8aOGaeyypa0JaaGinai % aacUdacaaMc8+aa8qmaeaacaWGNbWaaeWaaeaacaWG4baacaGLOaGa % ayzkaaGaaeizaiaadIhaaSqaaiaaigdaaeaacaaIZaaaniabgUIiYd % GccqGH9aqpcaaIYaaaaa!5093! \Leftrightarrow \int_1^3 {f\left( x \right){\rm{d}}x} = 4;\,\int_1^3 {g\left( x \right){\rm{d}}x} = 2\) suy ra \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Lq-Jirpepeea0-as0Fb9pgea0lXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaapedabaWaam % WaaeaacaWGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaey4kaSIa % am4zamaabmaabaGaamiEaaGaayjkaiaawMcaaaGaay5waiaaw2faai % aabsgacaWG4baaleaacaaIXaaabaGaaG4maaqdcqGHRiI8aOGaeyyp % a0JaaGOnaaaa!4773! \int_1^3 {\left[ {f\left( x \right) + g\left( x \right)} \right]{\rm{d}}x} = 6\)

Ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqaMLgvLHfij5gC1rhimfMBNvxyNvga7TNm951EYG % xlX0xFTWLzYf2y7ftF7HtF9adxmvMz0jxANHgDHjNCVDhi7TNm951E % YGxlX0xF9S3EY0Nx71Ym91hxmvMz0jxANHgDHjNCVDhi41tlXaWexL % MBbXgBcf2CPn2qVrwzqf2zLnharuavP1wzZbItLDhis9wBH5garmWu % 51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlNi-xH8 % yiVC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbbG8FasPYRqj % 0-yi0dXdbba9pGe9xq-JbbG8A8frFve9Fve9Ff0dmeaabaqaciGaca % GaaeqabaWaaeaaeaaakeaaqaaaaaaaaaWdbiaaikdapaWaaWbaaSqa % beaapeGaaGOmaiaadIhacqGHsislcaaIXaaaaOGaeyOeI0YaaSaaa8 % aabaWdbiaaigdaa8aabaWdbiaaiIdaaaGaeyypa0JaaGimaiabgsDi % BlaaikdapaWaaWbaaSqabeaapeGaaGOmaiaadIhacqGHsislcaaIXa % aaaOGaeyypa0JaaGOma8aadaahaaWcbeqaa8qacqGHsislcaaIZaaa % aOGaeyi1HSTaamiEaiabg2da9iabgkHiTiaaigdaaaa!7693! {2^{2x - 1}} - \frac{1}{8} = 0 \Leftrightarrow {2^{2x - 1}} = {2^{ - 3}} \Leftrightarrow x = - 1\)

Tập xác định của hàm số: D =R.

Đạo hàm: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafa % Gaeyypa0JaaGinaiaadIhadaahaaWcbeqaaiaaiodaaaGccqGHRaWk % caaI0aGaamiEaaaa!3D50! y' = 4{x^3} + 4x\) ;\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafa % Gaeyypa0JaaGimaiabgsDiBlaadIhacqGH9aqpcaaIWaaaaa!3DD7! y' = 0 \Leftrightarrow x = 0\) .

Bảng biến thiên:

Vậy hàm số đã cho có một điểm cực trị.

Tiệm cận đứng là x = -1; tiệm cận ngang y = 1 nên I(-1;1) .

Gọi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamytamaaBa % aaleaacaaIWaaabeaakmaabmaabaGaamiEamaaBaaaleaacaaIWaaa % beaakiaacUdacaqGGaWaaSaaaeaacaWG4bWaaSbaaSqaaiaaicdaae % qaaOGaey4kaSIaaGOmaaqaaiaadIhadaWgaaWcbaGaaGimaaqabaGc % cqGHRaWkcaaIXaaaaaGaayjkaiaawMcaaiabgIGiopaabmaabaGaam % 4qaaGaayjkaiaawMcaaaaa!4788! {M_0}\left( {{x_0};{\rm{ }}\frac{{{x_0} + 2}}{{{x_0} + 1}}} \right) \in \left( C \right)\);\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyypa0JaeyOeI0YaaSaa % aeaacaaIXaaabaWaaeWaaeaacaWG4bGaey4kaSIaaGymaaGaayjkai % aawMcaamaaCaaaleqabaGaaGOmaaaaaaaaaa!413B! f'\left( x \right) = - \frac{1}{{{{\left( {x + 1} \right)}^2}}}\)  nên phương trình tiếp tuyến của (C) là:

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabgk % HiTmaalaaabaGaamiEamaaBaaaleaacaaIWaaabeaakiabgUcaRiaa % ikdaaeaacaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaey4kaSIaaGymaa % aacqGH9aqpcqGHsisldaWcaaqaaiaaigdaaeaadaqadaqaaiaadIha % daWgaaWcbaGaaGimaaqabaGccqGHRaWkcaaIXaaacaGLOaGaayzkaa % WaaWbaaSqabeaacaaIYaaaaaaakmaabmaabaGaamiEaiabgkHiTiaa % dIhadaWgaaWcbaGaaGimaaqabaaakiaawIcacaGLPaaacqGHuhY2da % WcaaqaaiaaigdaaeaadaqadaqaaiaadIhadaWgaaWcbaGaaGimaaqa % baGccqGHRaWkcaaIXaaacaGLOaGaayzkaaWaaWbaaSqabeaacaaIYa % aaaaaakiaadIhacqGHRaWkcaWG5bGaeyOeI0YaaSaaaeaacaWG4bWa % a0baaSqaaiaaicdaaeaacaaIYaaaaOGaey4kaSIaaGinaiaadIhada % WgaaWcbaGaaGimaaqabaGccqGHRaWkcaaIYaaabaWaaeWaaeaacaWG % 4bWaaSbaaSqaaiaaicdaaeqaaOGaey4kaSIaaGymaaGaayjkaiaawM % caamaaCaaaleqabaGaaGOmaaaaaaGccqGH9aqpcaaIWaaaaa!69CA! y - \frac{{{x_0} + 2}}{{{x_0} + 1}} = - \frac{1}{{{{\left( {{x_0} + 1} \right)}^2}}}\left( {x - {x_0}} \right) \Leftrightarrow \frac{1}{{{{\left( {{x_0} + 1} \right)}^2}}}x + y - \frac{{x_0^2 + 4{x_0} + 2}}{{{{\left( {{x_0} + 1} \right)}^2}}} = 0\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizamaabm % aabaGaamysaiaacYcacaqGGaGaeyiLdqeacaGLOaGaayzkaaGaeyyp % a0ZaaSaaaeaadaabdaqaaiabgkHiTmaalaaabaGaaGymaaqaamaabm % aabaGaamiEamaaBaaaleaacaaIWaaabeaakiabgUcaRiaaigdaaiaa % wIcacaGLPaaadaahaaWcbeqaaiaaikdaaaaaaOGaey4kaSIaaGymai % abgkHiTmaalaaabaGaamiEamaaDaaaleaacaaIWaaabaGaaGOmaaaa % kiabgUcaRiaaisdacaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaey4kaS % IaaGOmaaqaamaabmaabaGaamiEamaaBaaaleaacaaIWaaabeaakiab % gUcaRiaaigdaaiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaaaaa % GccaGLhWUaayjcSdaabaWaaOaaaeaadaWcaaqaaiaaigdaaeaadaqa % daqaaiaadIhadaWgaaWcbaGaaGimaaqabaGccqGHRaWkcaaIXaaaca % GLOaGaayzkaaWaaWbaaSqabeaacaaI0aaaaaaakiabgUcaRiaaigda % aSqabaaaaOGaeyypa0ZaaSaaaeaacaaIYaWaaqWaaeaacaWG4bWaaS % baaSqaaiaaicdaaeqaaOGaey4kaSIaaGymaaGaay5bSlaawIa7aaqa % amaakaaabaWaaeWaaeaacaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaey % 4kaSIaaGymaaGaayjkaiaawMcaamaaCaaaleqabaGaaGinaaaakiab % gUcaRiaaigdaaSqabaaaaOGaeyizImQaaGOmamaakaaabaWaaSaaae % aadaqadaqaaiaadIhadaWgaaWcbaGaaGimaaqabaGccqGHRaWkcaaI % XaaacaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaaGcbaGaaGOmam % aakaaabaWaaeWaaeaacaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaey4k % aSIaaGymaaGaayjkaiaawMcaamaaCaaaleqabaGaaGinaaaaaeqaaa % aaaeqaaOGaeyypa0ZaaOaaaeaacaaIYaaaleqaaaaa!827E! d\left( {I,{\rm{ }}\Delta } \right) = \frac{{\left| { - \frac{1}{{{{\left( {{x_0} + 1} \right)}^2}}} + 1 - \frac{{x_0^2 + 4{x_0} + 2}}{{{{\left( {{x_0} + 1} \right)}^2}}}} \right|}}{{\sqrt {\frac{1}{{{{\left( {{x_0} + 1} \right)}^4}}} + 1} }} = \frac{{2\left| {{x_0} + 1} \right|}}{{\sqrt {{{\left( {{x_0} + 1} \right)}^4} + 1} }} \le 2\sqrt {\frac{{{{\left( {{x_0} + 1} \right)}^2}}}{{2\sqrt {{{\left( {{x_0} + 1} \right)}^4}} }}} = \sqrt 2 \)

Dựa vào bảng biến thiên ta thấy hàm số nghịch biến trên khoảng (-1;1)

Gọi H là trung điểm của AB, suy ra \(SH \bot \left( {ABCD} \right)\).

Gọi G là trọng tâm tam giác \(\Delta SAB\) và O là tâm hình vuông ABCD.

Từ G kẻ GI // HO suy ra GI là trục đường tròn ngoại tiếp tam giác \(\Delta SAB\) và từ O kẻ OI // SH thì OI là trục đường tròn ngoại tiếp hình vuông ABCD.

Ta có hai đường này cùng nằm trong mặt phẳng và cắt nhau tại I.

Suy ra I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.

\( R = SI = \sqrt {S{G^2} + G{I^2}} = \frac{{a\sqrt {21} }}{6}\)

Suy ra thể tích khối cầu ngoại tiếp khối chóp S.ABCD là . 

\(V = \frac{4}{3}\pi {R^3} = \frac{{7\sqrt {21} }}{{54}}\pi {a^3}\)

Ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOmamaaCa % aaleqabaGaamiEamaaCaaameqabaGaaGOmaaaaliabgkHiTiaaioda % caWG4bGaey4kaSIaaGOmaaaakiabg2da9iaaisdaaaa!3EE2! {2^{{x^2} - 3x + 2}} = 4\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % iEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaiodacaWG4bGaey4k % aSIaaGOmaiabg2da9iaaikdaaaa!4047! \Leftrightarrow {x^2} - 3x + 2 = 2\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aam % qaaeaafaqabeGabaaabaGaamiEaiabg2da9iaaicdaaeaacaWG4bGa % eyypa0JaaG4maaaaaiaawUfaaaaa!3ED5! \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0}\\ {x = 3} \end{array}} \right.\)

Vậy \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamivaiabg2 % da9iaadIhadaqhaaWcbaGaaGymaaqaaiaaiodaaaGccqGHRaWkcaWG % 4bWaa0baaSqaaiaaikdaaeaacaaIZaaaaaaa!3E04! T = x_1^3 + x_2^3=27\)

Ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaikdaaeqaaOWaaSaaaeaacaWG4bWaaWba % aSqabeaacaaIYaaaaOGaeyOeI0IaaGOnaiaadIhacqGHRaWkcaaI4a % aabaGaaGinaiaadIhacqGHsislcaaIXaaaaiabgwMiZkaaicdaaaa!45E6! {\log _2}\frac{{{x^2} - 6x + 8}}{{4x - 1}} \ge 0\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aaS % aaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaeyOeI0IaaGOnaiaa % dIhacqGHRaWkcaaI4aaabaGaaGinaiaadIhacqGHsislcaaIXaaaai % abgwMiZkaaigdaaaa!4481! \Leftrightarrow \frac{{{x^2} - 6x + 8}}{{4x - 1}} \ge 1\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aaS % aaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaeyOeI0IaaGymaiaa % icdacaWG4bGaey4kaSIaaGyoaaqaaiaaisdacaWG4bGaeyOeI0IaaG % ymaaaacqGHLjYScaaIWaaaaa!4536! \Leftrightarrow \frac{{{x^2} - 10x + 9}}{{4x - 1}} \ge 0\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aam % qaaqaabeqaamaaceaaeaqabeaacaWG4bWaaWbaaSqabeaacaaIYaaa % aOGaeyOeI0IaaGymaiaaicdacaWG4bGaey4kaSIaaGyoaiabgwMiZk % aaicdaaeaacaaI0aGaamiEaiabgkHiTiaaigdacqGH+aGpcaaIWaaa % aiaawUhaaaqaamaaceaaeaqabeaacaWG4bWaaWbaaSqabeaacaaIYa % aaaOGaeyOeI0IaaGymaiaaicdacaWG4bGaey4kaSIaaGyoaiabgsMi % JkaaicdaaeaacaaI0aGaamiEaiabgkHiTiaaigdacqGH8aapcaaIWa % aaaiaawUhaaaaacaGLBbaaaaa!58B0! \Leftrightarrow \left[ \begin{array}{l} \left\{ \begin{array}{l} {x^2} - 10x + 9 \ge 0\\ 4x - 1 > 0 \end{array} \right.\\ \left\{ \begin{array}{l} {x^2} - 10x + 9 \le 0\\ 4x - 1 < 0 \end{array} \right. \end{array} \right.\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aam % qaaqaabeqaamaalaaabaGaaGymaaqaaiaaisdaaaGaeyipaWJaamiE % aiabgsMiJkaaigdaaeaacaWG4bGaeyyzImRaaGyoaaaacaGLBbaaaa % a!42D1! \Leftrightarrow \left[ \begin{array}{l} \frac{1}{4} < x \le 1\\ x \ge 9 \end{array} \right.\)

Nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamivaiabg2 % da9maajadabaWaaSaaaeaacaaIXaaabaGaaGinaaaacaGG7aGaaGym % aaGaayjkaiaaw2faaiabgQIiipaajibabaGaaGyoaiaacUdacqGHRa % WkcqGHEisPaiaawUfacaGLPaaaaaa!440F! T = \left( {\frac{1}{4};1} \right] \cup \left[ {9; + \infty } \right)\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % ytaiabg2da9iaadggacqGHRaWkcaWGIbaaaa!3CD7! \Rightarrow M = a + b\) = 1+ 9 =10

Phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCa % aaleqabaGaaGOmaaaakiabgUcaRiaad2gacaWG4bGaeyOeI0IaamyB % aiabgUcaRiaaigdacqGH9aqpcaaIWaaaaa!3FF0! {x^2} + mx - m + 1 = 0\) có hai nghiệm trái dấu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % yyaiaadogacqGH8aapcaaIWaGaeyi1HSTaamyBaiabg6da+iaaigda % aaa!40ED! \Leftrightarrow ac < 0 \Leftrightarrow m > 1\).

Áp dụng phương trình mặt phẳng theo đoạn chắn ta có phương trình mặt phẳng là

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WG4baabaGaaGymaaaacqGHRaWkdaWcaaqaaiaadMhaaeaacaaIZaaa % aiabgUcaRmaalaaabaGaamOEaaqaaiaaikdaaaGaeyypa0JaaGymaa % aa!3ED7! \frac{x}{1} + \frac{y}{3} + \frac{z}{2} = 1\)

Ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqr1ngB % PrgifHhDYfgasaacH8srps0lbbf9q8WrFfeuY-Hhbba9q8qqaqFr0x % c9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8fr % Fve9Fve9Ff0dmeaabiqaceGabiGaaeaabaWaaeaaeaaakeaadaqada % qaaiaaikdadaahaaWcbeqaaiaadggaaaGccqGHRaWkdaWcaaqaaiaa % igdaaeaacaaIYaWaaWbaaSqabeaacaWGHbaaaaaaaOGaayjkaiaawM % caamaaCaaaleqabaGaaGOmaiaaicdacaaIXaGaaG4naaaakiabgsMi % JoaabmaabaGaaGOmamaaCaaaleqabaGaaGOmaiaaicdacaaIXaGaaG % 4naaaakiabgUcaRmaalaaabaGaaGymaaqaaiaaikdadaahaaWcbeqa % aiaaikdacaaIWaGaaGymaiaaiEdaaaaaaaGccaGLOaGaayzkaaWaaW % baaSqabeaacaWGHbaaaaaa!4F2D! {\left( {{2^a} + \frac{1}{{{2^a}}}} \right)^{2017}} \le {\left( {{2^{2017}} + \frac{1}{{{2^{2017}}}}} \right)^a}\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqr1ngB % PrgifHhDYfgasaacH8srps0lbbf9q8WrFfeuY-Hhbba9q8qqaqFr0x % c9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8fr % Fve9Fve9Ff0dmeaabiqaceGabiGaaeaabaWaaeaaeaaakeaacqGHsh % I3caaIYaGaaGimaiaaigdacaaI3aGaaeiBaiaab+gacaqGNbWaaSba % aSqaaiaaikdaaeqaaOWaaeWaaeaacaaIYaWaaWbaaSqabeaacaWGHb % aaaOGaey4kaSYaaSaaaeaacaaIXaaabaGaaGOmamaaCaaaleqabaGa % amyyaaaaaaaakiaawIcacaGLPaaacqGHKjYOcaWGHbGaaeiBaiaab+ % gacaqGNbWaaSbaaSqaaiaaikdaaeqaaOWaaeWaaeaacaaIYaWaaWba % aSqabeaacaaIYaGaaGimaiaaigdacaaI3aaaaOGaey4kaSYaaSaaae % aacaaIXaaabaGaaGOmamaaCaaaleqabaGaaGOmaiaaicdacaaIXaGa % aG4naaaaaaaakiaawIcacaGLPaaaaaa!58A0! \Rightarrow 2017{\rm{lo}}{{\rm{g}}_2}\left( {{2^a} + \frac{1}{{{2^a}}}} \right) \le a{\rm{lo}}{{\rm{g}}_2}\left( {{2^{2017}} + \frac{1}{{{2^{2017}}}}} \right)\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqr1ngB % PrgifHhDYfgasaacH8srps0lbbf9q8WrFfeuY-Hhbba9q8qqaqFr0x % c9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8fr % Fve9Fve9Ff0dmeaabiqaceGabiGaaeaabaWaaeaaeaaakeaacqGHsh % I3daWcaaqaaiaabYgacaqGVbGaae4zamaaBaaaleaacaaIYaaabeaa % kmaabmaabaGaaGOmamaaCaaaleqabaGaamyyaaaakiabgUcaRmaala % aabaGaaGymaaqaaiaaikdadaahaaWcbeqaaiaadggaaaaaaaGccaGL % OaGaayzkaaaabaGaamyyaaaacqGHKjYOdaWcaaqaaiaabYgacaqGVb % Gaae4zamaaBaaaleaacaaIYaaabeaakmaabmaabaGaaGOmamaaCaaa % leqabaGaaGOmaiaaicdacaaIXaGaaG4naaaakiabgUcaRmaalaaaba % GaaGymaaqaaiaaikdadaahaaWcbeqaaiaaikdacaaIWaGaaGymaiaa % iEdaaaaaaaGccaGLOaGaayzkaaaabaGaaGOmaiaaicdacaaIXaGaaG % 4naaaaaaa!58C0! \Rightarrow \frac{{{\rm{lo}}{{\rm{g}}_2}\left( {{2^a} + \frac{1}{{{2^a}}}} \right)}}{a} \le \frac{{{\rm{lo}}{{\rm{g}}_2}\left( {{2^{2017}} + \frac{1}{{{2^{2017}}}}} \right)}}{{2017}}\)

Xét hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqr1ngB % PrgifHhDYfgasaacH8srps0lbbf9q8WrFfeuY-Hhbba9q8qqaqFr0x % c9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8fr % Fve9Fve9Ff0dmeaabiqaceGabiGaaeaabaWaaeaaeaaakeaacaWG5b % Gaeyypa0JaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiabg2da % 9maalaaabaGaaeiBaiaab+gacaqGNbWaaSbaaSqaaiaaikdaaeqaaO % WaaeWaaeaacaaIYaWaaWbaaSqabeaacaWG4baaaOGaey4kaSYaaSaa % aeaacaaIXaaabaGaaGOmamaaCaaaleqabaGaamiEaaaaaaaakiaawI % cacaGLPaaaaeaacaWG4baaaiabg2da9maalaaabaGaaeiBaiaab+ga % caqGNbWaaSbaaSqaaiaaikdaaeqaaOWaaeWaaeaacaaI0aWaaWbaaS % qabeaacaWG4baaaOGaey4kaSIaaGymaaGaayjkaiaawMcaaiabgkHi % TiaadIhaaeaacaWG4baaaiabg2da9maalaaabaGaaeiBaiaab+gaca % qGNbWaaSbaaSqaaiaaikdaaeqaaOWaaeWaaeaacaaI0aWaaWbaaSqa % beaacaWG4baaaOGaey4kaSIaaGymaaGaayjkaiaawMcaaaqaaiaadI % haaaGaeyOeI0IaaGymaaaa!6311! y = f\left( x \right) = \frac{{{\rm{lo}}{{\rm{g}}_2}\left( {{2^x} + \frac{1}{{{2^x}}}} \right)}}{x} = \frac{{{\rm{lo}}{{\rm{g}}_2}\left( {{4^x} + 1} \right) - x}}{x} = \frac{{{\rm{lo}}{{\rm{g}}_2}\left( {{4^x} + 1} \right)}}{x} - 1\)

Ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqr1ngB % PrgifHhDYfgasaacH8srps0lbbf9q8WrFfeuY-Hhbba9q8qqaqFr0x % c9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8fr % Fve9Fve9Ff0dmeaabiqaceGabiGaaeaabaWaaeaaeaaakeaaceWG5b % GbauaacqGH9aqpdaWcaaqaaiaaigdaaeaacaqGSbGaaeOBaiaaikda % aaWaamWaaeaadaWcaaqaamaalaaabaWaaeWaaeaacaaI0aWaaWbaaS % qabeaacaWG4baaaOGaey4kaSIaaGymaaGaayjkaiaawMcaaiaacEca % aeaacaaI0aWaaWbaaSqabeaacaWG4baaaOGaey4kaSIaaGymaaaaca % GGUaGaamiEaiabgkHiTiaabYgacaqGUbWaaeWaaeaacaaI0aWaaWba % aSqabeaacaWG4baaaOGaey4kaSIaaGymaaGaayjkaiaawMcaaaqaai % aadIhadaahaaWcbeqaaiaaikdaaaaaaaGccaGLBbGaayzxaaGaeyyp % a0ZaaSaaaeaacaaIXaaabaGaaeiBaiaab6gacaaIYaaaamaadmaaba % WaaSaaaeaacaaI0aWaaWbaaSqabeaacaWG4baaaOGaaiOlaiaabYga % caqGUbGaaGinaiaac6cacaWG4bGaeyOeI0YaaeWaaeaacaaI0aWaaW % baaSqabeaacaWG4baaaOGaey4kaSIaaGymaaGaayjkaiaawMcaaiaa % bYgacaqGUbWaaeWaaeaacaaI0aWaaWbaaSqabeaacaWG4baaaOGaey % 4kaSIaaGymaaGaayjkaiaawMcaaaqaaiaadIhadaahaaWcbeqaaiaa % ikdaaaGcdaqadaqaaiaaisdadaahaaWcbeqaaiaadIhaaaGccqGHRa % WkcaaIXaaacaGLOaGaayzkaaaaaaGaay5waiaaw2faaiabgYda8iaa % icdaaaa!76D6! y' = \frac{1}{{{\rm{ln}}2}}\left[ {\frac{{\frac{{\left( {{4^x} + 1} \right)'}}{{{4^x} + 1}}.x - {\rm{ln}}\left( {{4^x} + 1} \right)}}{{{x^2}}}} \right] = \frac{1}{{{\rm{ln}}2}}\left[ {\frac{{{4^x}.{\rm{ln}}4.x - \left( {{4^x} + 1} \right){\rm{ln}}\left( {{4^x} + 1} \right)}}{{{x^2}\left( {{4^x} + 1} \right)}}} \right] < 0\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqr1ngB % PrgifHhDYfgasaacH8srps0lbbf9q8WrFfeuY-Hhbba9q8qqaqFr0x % c9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8fr % Fve9Fve9Ff0dmeaabiqaceGabiGaaeaabaWaaeaaeaaakeaaceWG5b % GbauaacqGH9aqpdaWcaaqaaiaaigdaaeaacaqGSbGaaeOBaiaaikda % aaWaamWaaeaadaWcaaqaaiaaisdadaahaaWcbeqaaiaadIhaaaGcca % GGUaGaaeiBaiaab6gacaaI0aWaaWbaaSqabeaacaWG4baaaOGaeyOe % I0YaaeWaaeaacaaI0aWaaWbaaSqabeaacaWG4baaaOGaey4kaSIaaG % ymaaGaayjkaiaawMcaaiaabYgacaqGUbWaaeWaaeaacaaI0aWaaWba % aSqabeaacaWG4baaaOGaey4kaSIaaGymaaGaayjkaiaawMcaaaqaai % aadIhadaahaaWcbeqaaiaaikdaaaGcdaqadaqaaiaaisdadaahaaWc % beqaaiaadIhaaaGccqGHRaWkcaaIXaaacaGLOaGaayzkaaaaaaGaay % 5waiaaw2faaiabgYda8iaaicdaaaa!5B06! y' = \frac{1}{{{\rm{ln}}2}}\left[ {\frac{{{4^x}.{\rm{ln}}{4^x} - \left( {{4^x} + 1} \right){\rm{ln}}\left( {{4^x} + 1} \right)}}{{{x^2}\left( {{4^x} + 1} \right)}}} \right] < 0\) \(;% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqr1ngB % PrgifHhDYfgasaacH8srps0lbbf9q8WrFfeuY-Hhbba9q8qqaqFr0x % c9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8fr % Fve9Fve9Ff0dmeaabiqaceGabiGaaeaabaWaaeaaeaaakeaacqGHai % IicaWG4bGaeyOpa4JaaGimaaaa!3AE3! \forall x > 0\)

Nên y = f(x) là hàm giảm trên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqr1ngB % PrgifHhDYfgasaacH8srps0lbbf9q8WrFfeuY-Hhbba9q8qqaqFr0x % c9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8fr % Fve9Fve9Ff0dmeaabaqaceGabiGaaeaabaWaaeaaeaaakeaadaqada % qaaiaaicdacaGG7aGaey4kaSIaeyOhIukacaGLOaGaayzkaaaaaa!3CA7! \left( {0; + \infty } \right)\).

Do đó \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqr1ngB % PrgifHhDYfgasaacH8srps0lbbf9q8WrFfeuY-Hhbba9q8qqaqFr0x % c9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8fr % Fve9Fve9Ff0dmeaabiqaceGabiGaaeaabaWaaeaaeaaakeaacaWGMb % WaaeWaaeaacaWGHbaacaGLOaGaayzkaaGaeyizImQaamOzamaabmaa % baGaaGOmaiaaicdacaaIXaGaaG4naaGaayjkaiaawMcaaaaa!41C9! f\left( a \right) \le f\left( {2017} \right)\), ( a > 0)  khi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqr1ngB % PrgifHhDYfgasaacH8srps0lbbf9q8WrFfeuY-Hhbba9q8qqaqFr0x % c9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8fr % Fve9Fve9Ff0dmeaabiqaceGabiGaaeaabaWaaeaaeaaakeaacaaIWa % GaeyipaWJaamyyaiabgsMiJkaaikdacaaIWaGaaGymaiaaiEdaaaa!3E9F! 0 < a \le 2017\).

Gọi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOEaiabg2 % da9iaadIhacqGHRaWkcaWGPbGaamyEaaaa!3BC4! z = x + iy\) với \( x, y \in R\) ta có hệ phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaqaabe % qaamaaemaabaGaamOEaiabgkHiTiaaikdaaiaawEa7caGLiWoacqGH % 9aqpdaabdaqaaiaadQhaaiaawEa7caGLiWoaaeaadaqadaqaaiaadQ % hacqGHRaWkcaaIXaaacaGLOaGaayzkaaWaaeWaaeaaceWG6bGbaeba % cqGHsislcaWGPbaacaGLOaGaayzkaaGaeyicI4SaeSyhHekaaiaawU % haaaaa!4D9A! \left\{ \begin{array}{l} \left| {z - 2} \right| = \left| z \right|\\ \left( {z + 1} \right)\left( {\bar z - i} \right) \in R \end{array} \right.\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aai % qaaqaabeqaamaabmaabaGaamiEaiabgkHiTiaaikdaaiaawIcacaGL % PaaadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaWG5bWaaWbaaSqabe % aacaaIYaaaaOGaeyypa0JaamiEamaaCaaaleqabaGaaGOmaaaakiab % gUcaRiaadMhadaahaaWcbeqaaiaaikdaaaaakeaadaqadaqaaiaadI % hacqGHRaWkcaaIXaGaey4kaSIaamyAaiaadMhaaiaawIcacaGLPaaa % daqadaqaaiaadIhacqGHsislcaWGPbGaamyEaiabgkHiTiaadMgaai % aawIcacaGLPaaacqGHiiIZcqWIDesOaaGaay5Eaaaaaa!584E! \Leftrightarrow \left\{ \begin{array}{l} {\left( {x - 2} \right)^2} + {y^2} = {x^2} + {y^2}\\ \left( {x + 1 + iy} \right)\left( {x - iy - i} \right) \in R \end{array} \right.\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aai % qaaqaabeqaaiaadIhacqGH9aqpcaaIXaaabaWaaeWaaeaacqGHsisl % caWG4bGaeyOeI0IaaGymaaGaayjkaiaawMcaamaabmaabaGaamyEai % abgUcaRiaaigdaaiaawIcacaGLPaaacqGHRaWkcaWG4bGaamyEaiab % g2da9iaaicdaaaGaay5Eaaaaaa!4A0B! \Leftrightarrow \left\{ \begin{array}{l} x = 1\\ \left( { - x - 1} \right)\left( {y + 1} \right) + xy = 0 \end{array} \right.\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aai % qaaqaabeqaaiaadIhacqGH9aqpcaaIXaaabaGaamyEaiabg2da9iab % gkHiTiaaikdaaaGaay5Eaaaaaa!3FDC! \Leftrightarrow \left\{ \begin{array}{l} x = 1\\ y = - 2 \end{array} \right.\)\(\Rightarrow z = 1 - 2i\)

Gọi A là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi môn Hóa học”.

B là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi môn Vật lí”.

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiabgQ % Iiilaadkeaaaa!3920! A \cup B\) là biến cố “Học sinh được chọn đạt điểm tổng kết môn Hóa học hoặc Vật lí loại giỏi”.

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiabgM % Iihlaadkeaaaa!391E! A \cap B\) là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi cả hai môn Hóa học và Vật lí”.

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBamaabm % aabaGaamyqaiabgQIiilaadkeaaiaawIcacaGLPaaacqGH9aqpcaaI % WaGaaiilaiaaiwdacaGGUaGaaGinaiaaicdaaaa!40F5! n\left( {A \cup B} \right) = 0,5.40 = 20\)

Mặt khác: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBamaabm % aabaGaamyqaiabgQIiilaadkeaaiaawIcacaGLPaaacqGH9aqpcaWG % UbWaaeWaaeaacaWGbbaacaGLOaGaayzkaaGaey4kaSIaamOBamaabm % aabaGaamOqaaGaayjkaiaawMcaaiabgkHiTiaad6gadaqadaqaaiaa % dgeacaGGUaGaamOqaaGaayjkaiaawMcaaaaa!49B1! n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A.B} \right)\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % OBamaabmaabaGaamyqaiaac6cacaWGcbaacaGLOaGaayzkaaGaeyyp % a0JaamOBamaabmaabaGaamyqaaGaayjkaiaawMcaaiabgUcaRiaad6 % gadaqadaqaaiaadkeaaiaawIcacaGLPaaacqGHsislcaWGUbWaaeWa % aeaacaWGbbGaeyOkIGSaamOqaaGaayjkaiaawMcaaaaa!4C0E! \Rightarrow n\left( {A.B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cup B} \right)\) = 12 + 13 - 20 = 5

Công thức số hạng tổng quát : \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyDamaaBa % aaleaacaWGUbaabeaakiabg2da9iaadwhadaWgaaWcbaGaaGymaaqa % baGccqGHRaWkdaqadaqaaiaad6gacqGHsislcaaIXaaacaGLOaGaay % zkaaGaamizaaaa!40F6! {u_n} = {u_1} + \left( {n - 1} \right)d\), \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBaiabgw % MiZkaaikdaaaa!3968! n \ge 2\)

Ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aerbdfgBPjMCPbqeeuuDJXwAKbsr4rNCHbGeaGqiVu0Je9sqqrpepC % 0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs0-yq % aqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaaiaabe % qaamaaeaqbaaGcbaGaamOEamaaBaaaleaacaaIXaaabeaakiabgUca % RiaadQhadaWgaaWcbaGaaGOmaaqabaGccqGHRaWkcaWG6bWaaSbaaS % qaaiaaiodaaeqaaOGaeyypa0JaeyOeI0IaamyyaiabgsDiBlaaisda % caWG3bGaey4kaSIaaGymaiaaikdacaWGPbGaeyOeI0IaaGinaiabg2 % da9iabgkHiTiaadggaaaa!5340! {z_1} + {z_2} + {z_3} = - a \Leftrightarrow 4w + 12i - 4 = - a\) là số thực, suy ra w có phần ảo 3i hay w = m - 3i.

Khi đó \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aerbdfgBPjMCPbqeeuuDJXwAKbsr4rNCHbGeaGqiVu0Je9sqqrpepC % 0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs0-yq % aqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaaiaabe % qaamaaeaqbaaGcbaGaamOEamaaBaaaleaacaaIXaaabeaakiabg2da % 9iaad2gacaGG7aGaaGPaVlaaykW7caWG6bWaaSbaaSqaaiaaikdaae % qaaOGaeyypa0JaamyBaiabgUcaRiaaiAdacaWGPbGaai4oaiaaykW7 % caWG6bWaaSbaaSqaaiaaiodaaeqaaOGaeyypa0JaaGOmaiaad2gacq % GHsislcaaI2aGaamyAaiabgkHiTiaaisdaaaa!565B! {z_1} = m;\,\,{z_2} = m + 6i;\,{z_3} = 2m - 6i - 4\) mà \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aerbdfgBPjMCPbqeeuuDJXwAKbsr4rNCHbGeaGqiVu0Je9sqqrpepC % 0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs0-yq % aqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaaiaabe % qaamaaeaqbaaGcbaGaamOEamaaBaaaleaacaaIZaaabeaakiaacUda % caaMc8UaaGPaVlaadQhadaWgaaWcbaGaaGOmaaqabaaaaa!449D! {z_3};\,\,{z_2}\) là liên hợp của nhau nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aerbdfgBPjMCPbqeeuuDJXwAKbsr4rNCHbGeaGqiVu0Je9sqqrpepC % 0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs0-yq % aqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaaiaabe % qaamaaeaqbaaGcbaGaamyBaiabg2da9iaaikdacaWGTbGaeyOeI0Ia % aGinaiabgsDiBlaad2gacqGH9aqpcaaI0aaaaa!4752! m = 2m - 4 \Leftrightarrow m = 4\).

Vậy \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aerbdfgBPjMCPbqeeuuDJXwAKbsr4rNCHbGeaGqiVu0Je9sqqrpepC % 0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs0-yq % aqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaaiaabe % qaamaaeaqbaaGcbaGaamOEamaaBaaaleaacaaIXaaabeaakiabg2da % 9iaaisdacaGG7aGaaGPaVlaaykW7caWG6bWaaSbaaSqaaiaaikdaae % qaaOGaeyypa0JaaGinaiabgUcaRiaaiAdacaWGPbGaai4oaiaaykW7 % caWG6bWaaSbaaSqaaiaaiodaaeqaaOGaeyypa0JaaGinaiabgkHiTi % aaiAdacaWGPbaaaa!5358! {z_1} = 4;\,\,{z_2} = 4 + 6i;\,{z_3} = 4 - 6i\).

Theo Viet ta có.

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aerbdfgBPjMCPbqeeuuDJXwAKbsr4rNCHbGeaGqiVu0Je9sqqrpepC % 0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs0-yq % aqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaaiaabe % qaamaaeaqbaaGcbaWaaiqaaqaabeqaaiaadQhadaWgaaWcbaGaaGym % aaqabaGccqGHRaWkcaWG6bWaaSbaaSqaaiaaikdaaeqaaOGaey4kaS % IaamOEamaaBaaaleaacaaIZaaabeaakiabg2da9iabgkHiTiaadgga % aeaacaWG6bWaaSbaaSqaaiaaigdaaeqaaOGaamOEamaaBaaaleaaca % aIYaaabeaakiabgUcaRiaadQhadaWgaaWcbaGaaGOmaaqabaGccaWG % 6bWaaSbaaSqaaiaaiodaaeqaaOGaey4kaSIaamOEamaaBaaaleaaca % aIXaaabeaakiaadQhadaWgaaWcbaGaaG4maaqabaGccqGH9aqpcaWG % IbaabaGaamOEamaaBaaaleaacaaIXaaabeaakiaadQhadaWgaaWcba % GaaGOmaaqabaGccaWG6bWaaSbaaSqaaiaaiodaaeqaaOGaeyypa0Ja % eyOeI0Iaam4yaaaacaGL7baacqGHshI3daGabaabaeqabaGaamyyai % abg2da9iabgkHiTiaaigdacaaIYaaabaGaamOyaiabg2da9iaaiIda % caaI0aaabaGaam4yaiabg2da9iabgkHiTiaaikdacaaIWaGaaGioaa % aacaGL7baaaaa!70D5! \left\{ \begin{array}{l} {z_1} + {z_2} + {z_3} = - a\\ {z_1}{z_2} + {z_2}{z_3} + {z_1}{z_3} = b\\ {z_1}{z_2}{z_3} = - c \end{array} \right. \Rightarrow \left\{ \begin{array}{l} a = - 12\\ b = 84\\ c = - 208 \end{array} \right.\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aerbdfgBPjMCPbqeeuuDJXwAKbsr4rNCHbGeaGqiVu0Je9sqqrpepC % 0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs0-yq % aqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaaiaabe % qaamaaeaqbaaGcbaGaamiuaiabg2da9maaemaabaGaeyOeI0IaaGym % aiaaikdacqGHRaWkcaaI4aGaaGinaiabgkHiTiaaikdacaaIWaGaaG % ioaaGaay5bSlaawIa7aiabg2da9iaaigdacaaIZaGaaGOnaaaa!4D14! P = \left| { - 12 + 84 - 208} \right| = 136\)

Nếu hàm số đạt cực trị tại \(x_0\) thì hàm số không có đạo hàm tại \(x_0 \) hoặc \(f'(x_0) = 0\)

Vì d đi qua A, vuông góc với (P) nên d có một vectơ chỉ phương là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8Haaeaaca % WGHbaacaGLxdcacqGH9aqpdaqadaqaaiaaikdacaGG7aGaeyOeI0Ia % aGymaiaacUdacaaIZaaacaGLOaGaayzkaaaaaa!3FBB! \overrightarrow a = \left( {2; - 1;3} \right)\).

* Vậy phương trình tham số của d là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaqaabe % qaaiaadIhacqGH9aqpcaaIXaGaey4kaSIaaGOmaiaadshaaeaacaWG % 5bGaeyypa0JaeyOeI0IaaG4maiabgkHiTiaadshaaeaacaWG6bGaey % ypa0JaaGOmaiabgUcaRiaaiodacaWG0baaaiaawUhaaaaa!4757! \left\{ \begin{array}{l} x = 1 + 2t\\ y = - 3 - t\\ z = 2 + 3t \end{array} \right.\)

Gọi I là trung điểm đoạn AB \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % ysamaabmaabaGaeyOeI0IaaGymaiaacUdacaaIWaGaai4oaiabgkHi % TiaaigdaaiaawIcacaGLPaaaaaa!4030! \Rightarrow I\left( { - 1;0; - 1} \right)\).

Mặt cầu cần tìm có tâm \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysamaabm % aabaGaeyOeI0IaaGymaiaacUdacaaIWaGaai4oaiabgkHiTiaaigda % aiaawIcacaGLPaaaaaa!3DD3! I\left( { - 1;0; - 1} \right)\)

và bán kính \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOuaiabg2 % da9iaadMeacaWGbbGaeyypa0ZaaOaaaeaadaqadaqaaiabgkHiTiaa % igdacqGHRaWkcaaIZaaacaGLOaGaayzkaaWaaWbaaSqabeaacaaIYa % aaaOGaey4kaSYaaeWaaeaacaaIWaGaeyOeI0IaaGymaaGaayjkaiaa % wMcaamaaCaaaleqabaGaaGOmaaaakiabgUcaRmaabmaabaGaeyOeI0 % IaaGymaiabgUcaRiaaisdaaiaawIcacaGLPaaadaahaaWcbeqaaiaa % ikdaaaaabeaakiabg2da9maakaaabaGaaGymaiaaisdaaSqabaaaaa!4F3E! R = IA = \sqrt {{{\left( { - 1 + 3} \right)}^2} + {{\left( {0 - 1} \right)}^2} + {{\left( { - 1 + 4} \right)}^2}} = \sqrt {14} \).

Ta có phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WG4bGaey4kaSIaaGymaaGaayjkaiaawMcaamaaCaaaleqabaGaaGOm % aaaakiabgUcaRiaadMhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkda % qadaqaaiaadQhacqGHRaWkcaaIXaaacaGLOaGaayzkaaWaaWbaaSqa % beaacaaIYaaaaOGaeyypa0JaaGymaiaaisdacaGGUaaaaa!4707! {\left( {x + 1} \right)^2} + {y^2} + {\left( {z + 1} \right)^2} = 14.\)

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aebbfv3ySLgzGueE0jxyaibaieYlh9qrpeeu0dXdh9vqqj-hEeeu0x % Xdbba9frFj0-OqFfea0dXdd9vqaq-JfrVkFHe9pgea0dXdar-Jb9hs % 0dXdbPYxe9vr0-vr0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaO % qaamaalaaabaGaamOvamaaBaaaleaacaWGebGaaiOlaiaad2eacaWG % obGaamiuaaqabaaakeaacaWGwbWaaSbaaSqaaiaadseacaGGUaGaam % isaiaadMeacaWGlbaabeaaaaGccqGH9aqpdaWcaaqaaiaadseacaWG % nbaabaGaamiraiaadIeaaaGaaiOlamaalaaabaGaamiraiaad6eaae % aacaWGebGaamysaaaacaGGUaWaaSaaaeaacaWGebGaamiuaaqaaiaa % dseacaWGlbaaaiabg2da9maabmaabaWaaSaaaeaacaaIYaaabaGaaG % 4maaaaaiaawIcacaGLPaaadaahaaWcbeqaaiaaiodaaaaaaa!54C5! \frac{{{V_{D.MNP}}}}{{{V_{D.HIK}}}} = \frac{{DM}}{{DH}}.\frac{{DN}}{{DI}}.\frac{{DP}}{{DK}} = {\left( {\frac{2}{3}} \right)^3}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aebbfv3ySLgzGueE0jxyaibaieYlh9qrpeeu0dXdh9vqqj-hEeeu0x % Xdbba9frFj0-OqFfea0dXdd9vqaq-JfrVkFHe9pgea0dXdar-Jb9hs % 0dXdbPYxe9vr0-vr0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaO % qaaiabgkDiElaadAfadaWgaaWcbaGaamiraiaac6cacaWGnbGaamOt % aiaadcfaaeqaaOGaeyypa0ZaaSaaaeaacaaI4aaabaGaaGOmaiaaiE % daaaGaamOvamaaBaaaleaacaWGebGaaiOlaiaadIeacaWGjbGaam4s % aaqabaGccqGH9aqpdaWcaaqaaiaaiIdaaeaacaaIYaGaaG4naaaaca % GGUaWaaSaaaeaacaaIXaaabaGaaGinaaaacaGGUaGaamOvamaaBaaa % leaacaWGebGaaiOlaiaadgeacaWGcbGaam4qaaqabaGccqGH9aqpda % WcaaqaaiaaikdaaeaacaaIYaGaaG4naaaacaGGUaGaamOvamaaBaaa % leaacaWGebGaaiOlaiaadgeacaWGcbGaam4qaaqabaaaaa!5D2B! \Rightarrow {V_{D.MNP}} = \frac{8}{{27}}{V_{D.HIK}} = \frac{8}{{27}}.\frac{1}{4}.{V_{D.ABC}} = \frac{2}{{27}}.{V_{D.ABC}}\)

Ta có:\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aebbfv3ySLgzGueE0jxyaibaieYlh9qrpeeu0dXdh9vqqj-hEeeu0x % Xdbba9frFj0-OqFfea0dXdd9vqaq-JfrVkFHe9pgea0dXdar-Jb9hs % 0dXdbPYxe9vr0-vr0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaO % qaaiaadAfadaWgaaWcbaGaamiraiaac6cacaWGbbGaamOqaiaadoea % aeqaaOGaeyypa0ZaaSaaaeaacaaIXaaabaGaaG4maaaacaGGUaGaam % 4uamaaBaaaleaacaWGbbGaamOqaiaadoeaaeqaaOGaaiOlaiaadsea % caWGfbaaaa!474B! {V_{D.ABC}} = \frac{1}{3}.{S_{ABC}}.DE\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aebbfv3ySLgzGueE0jxyaibaieYlh9qrpeeu0dXdh9vqqj-hEeeu0x % Xdbba9frFj0-OqFfea0dXdd9vqaq-JfrVkFHe9pgea0dXdar-Jb9hs % 0dXdbPYxe9vr0-vr0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaO % qaaiabg2da9maalaaabaGaaGymaaqaaiaaiodaaaGaaiOlamaalaaa % baGaaGymaaqaaiaaikdaaaGaaiOlaiaadgeacaWGcbGaaiOlaiaadg % eacaWGdbGaaiOlaiGacohacaGGPbGaaiOBaiaadgeacaGGUaGaamir % aiaadweaaaa!495D! = \frac{1}{3}.\frac{1}{2}.AB.AC.\sin A.DE\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aebbfv3ySLgzGueE0jxyaibaieYlh9qrpeeu0dXdh9vqqj-hEeeu0x % Xdbba9frFj0-OqFfea0dXdd9vqaq-JfrVkFHe9pgea0dXdar-Jb9hs % 0dXdbPYxe9vr0-vr0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaO % qaaiabgsMiJoaalaaabaGaaGymaaqaaiaaiAdaaaGaamyqaiaadkea % caGGUaGaamyqaiaadoeacaGGUaGaamiraiaadweaaaa!42D4! \le \frac{1}{6}AB.AC.DE\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aebbfv3ySLgzGueE0jxyaibaieYlh9qrpeeu0dXdh9vqqj-hEeeu0x % Xdbba9frFj0-OqFfea0dXdd9vqaq-JfrVkFHe9pgea0dXdar-Jb9hs % 0dXdbPYxe9vr0-vr0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaO % qaaiabgsMiJoaalaaabaGaaGymaaqaaiaaiAdaaaGaamyqaiaadkea % caGGUaGaamyqaiaadoeacaGGUaGaamiraiaadgeaaaa!42D0! \le \frac{1}{6}AB.AC.DA\)

DE  là đường cao của hình chóp D.ABC

Dấu bằng xảy ra khi: DA = DE và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aebbfv3ySLgzGueE0jxyaibaieYlh9qrpeeu0dXdh9vqqj-hEeeu0x % Xdbba9frFj0-OqFfea0dXdd9vqaq-JfrVkFHe9pgea0dXdar-Jb9hs % 0dXdbPYxe9vr0-vr0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaO % qaamaaHaaabaGaamOqaiaadgeacaWGdbaacaGLcmaacqGH9aqpcaaI % 5aGaaGimamaaCaaaleqabaGaeSigI8gaaaaa!4083! \widehat {BAC} = {90^ \circ }\)

Suy ra:\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aebbfv3ySLgzGueE0jxyaibaieYlh9qrpeeu0dXdh9vqqj-hEeeu0x % Xdbba9frFj0-OqFfea0dXdd9vqaq-JfrVkFHe9pgea0dXdar-Jb9hs % 0dXdbPYxe9vr0-vr0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaO % qaamaabmaabaGaamOvamaaBaaaleaacaWGebGaaiOlaiaadgeacaWG % cbGaam4qaaqabaaakiaawIcacaGLPaaadaWgaaWcbaGaciyBaiaacg % gacaGG4baabeaakiabg2da9maalaaabaGaaGymaaqaaiaaiodaaaGa % aiOlamaalaaabaGaaGymaaqaaiaaikdaaaGaaiOlaiaadgeacaWGcb % GaaiOlaiaadgeacaWGdbGaaiOlaiaadseacaWGbbGaeyypa0ZaaSaa % aeaacaaIXaaabaGaaGOnaaaacaGGUaGaaG4maiaadggacaGGUaGaaG % inaiaadggacaGGUaGaaGynaiaadggacqGH9aqpcaaIXaGaaGimaiaa % dggadaahaaWcbeqaaiaaiodaaaaaaa!5C5A! {\left( {{V_{D.ABC}}} \right)_{\max }} = \frac{1}{3}.\frac{1}{2}.AB.AC.DA = \frac{1}{6}.3a.4a.5a = 10{a^3}\)

Vây: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aebbfv3ySLgzGueE0jxyaibaieYlh9qrpeeu0dXdh9vqqj-hEeeu0x % Xdbba9frFj0-OqFfea0dXdd9vqaq-JfrVkFHe9pgea0dXdar-Jb9hs % 0dXdbPYxe9vr0-vr0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaO % qaaiaadAfadaWgaaWcbaGaamiraiaac6cacaWGnbGaamOtaiaadcfa % aeqaaOGaeyypa0ZaaSaaaeaacaaIYaaabaGaaGOmaiaaiEdaaaGaai % OlaiaaigdacaaIWaGaamyyamaaCaaaleqabaGaaG4maaaakiabg2da % 9maalaaabaGaaGOmaiaaicdaaeaacaaIYaGaaG4naaaacaWGHbWaaW % baaSqabeaacaaIZaaaaaaa!4BB1! {V_{D.MNP}} = \frac{2}{{27}}.10{a^3} = \frac{{20}}{{27}}{a^3}\)

Ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8Haaeaaca % WGbbGaamOqaaGaay51GaGaeyypa0ZaaeWaaeaacqGHsislcaaIZaGa % ai4oaiabgkHiTiaaigdacaGG7aGaaGimaaGaayjkaiaawMcaaaaa!414E! \overrightarrow {AB} = \left( { - 3; - 1;0} \right)\); \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysamaabm % aabaWaaSaaaeaacaaIZaaabaGaaGOmaaaacaGG7aWaaSaaaeaacaaI % 1aaabaGaaGOmaaaacaGG7aGaaGymaaGaayjkaiaawMcaaaaa!3D98! I\left( {\frac{3}{2};\frac{5}{2};1} \right)\) là trung điểm của AB.

Gọi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq % aHXoqyaiaawIcacaGLPaaaaaa!391C! \left( \alpha \right)\) là mặt phẳng trung trực của AB và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdqKaey % ypa0ZaaeWaaeaacqaHXoqyaiaawIcacaGLPaaacqGHPiYXdaqadaqa % aiaadcfaaiaawIcacaGLPaaaaaa!3F84! \Delta = \left( \alpha \right) \cap \left( P \right)\). Khi đó \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdqeaaa!375A! \Delta \) chính là đường thẳng thuộc mặt phẳng (P) và cách đều hai điểm A,B.

Phương trình mặt phẳng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq % aHXoqyaiaawIcacaGLPaaaaaa!391C! \left( \alpha \right)\) đi qua \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysamaabm % aabaWaaSaaaeaacaaIZaaabaGaaGOmaaaacaGG7aWaaSaaaeaacaaI % 1aaabaGaaGOmaaaacaGG7aGaaGymaaGaayjkaiaawMcaaaaa!3D98! I\left( {\frac{3}{2};\frac{5}{2};1} \right)\) và có véc tơ pháp tuyến  là:\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8Haaeaaca % WGbbGaamOqaaGaay51GaGaeyypa0ZaaeWaaeaacqGHsislcaaIZaGa % ai4oaiabgkHiTiaaigdacaGG7aGaaGimaaGaayjkaiaawMcaaaaa!414E! \overrightarrow {AB} = \left( { - 3; - 1;0} \right)\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyOeI0IaaG % 4mamaabmaabaGaamiEaiabgkHiTmaalaaabaGaey4mamdabaGaaGOm % aaaaaiaawIcacaGLPaaacqGHsisldaqadaqaaiaadMhacqGHsislda % WcaaqaaiaaiwdaaeaacaaIYaaaaaGaayjkaiaawMcaaiabg2da9iaa % icdacqGHuhY2caaIZaGaamiEaiabgUcaRiaadMhacqGHsislcaaI3a % Gaeyypa0JaaGimaaaa!4DDF! - 3\left( {x - \frac{3}{2}} \right) - \left( {y - \frac{5}{2}} \right) = 0 \Leftrightarrow 3x + y - 7 = 0\)

Khi đó d là đường giao tuyến của \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq % aHXoqyaiaawIcacaGLPaaaaaa!391C! \left( \alpha \right)\) và (P).

Véctơ chỉ phương của \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiaacQ % dadaWhcaqaaiaadwhadaWgaaWcbaGaamizaaqabaaakiaawEniaiab % g2da9maadmaabaWaa8HaaeaacaWGUbWaaSbaaSqaamaabmaabaGaeq % ySdegacaGLOaGaayzkaaaabeaaaOGaay51GaGaaiilamaaFiaabaGa % amOBamaaBaaaleaadaqadaqaaiaadcfaaiaawIcacaGLPaaaaeqaaa % GccaGLxdcaaiaawUfacaGLDbaacqGH9aqpdaqadaqaaiabgkHiTiaa % igdacaGG7aGaaG4maiaacUdacqGHsislcaaIYaaacaGLOaGaayzkaa % Gaeyypa0JaeyOeI0YaaeWaaeaacaaIXaGaai4oaiabgkHiTiaaioda % caGG7aGaaGOmaaGaayjkaiaawMcaaaaa!5A85! d:\overrightarrow {{u_d}} = \left[ {\overrightarrow {{n_{\left( \alpha \right)}}} ,\overrightarrow {{n_{\left( P \right)}}} } \right] = \left( { - 1;3; - 2} \right) = - \left( {1; - 3;2} \right)\), d  đi qua \(C(0;7;0)\).

Vậy d có phương trình tham số là: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaqaabe % qaaiaadIhacqGH9aqpcaWG0baabaGaamyEaiabg2da9iaaiEdacqGH % sislcaaIZaGaamiDaaqaaiaadQhacqGH9aqpcaaIYaGaamiDaaaaca % GL7baaaaa!4334! \left\{ \begin{array}{l} x = t\\ y = 7 - 3t\\ z = 2t \end{array} \right.\) ( t là tham số).

Hình lập phương có 8 đỉnh, 12 cạnh và 6 mặt.

Vậy tổng số đỉnh, số cạnh và số mặt của hình lập phương là 26.

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaOaaaeaaca % aIZaaaleqaaOGaeyycI8SaeSijHikaaa!39D3! \sqrt 3 \notin Z\) nên hàm số xác định khi và chỉ khi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOmaiabgk % HiTiaadIhacqGH+aGpcaaIWaaaaa!3A5C! 2 - x > 0\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % iEaiabgYda8iaaikdaaaa!3B0D! \Leftrightarrow x < 2\)

Vậy tập xác định của hàm số là: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiraiabg2 % da9maabmaabaGaeyOeI0IaeyOhIuQaai4oaiaaikdaaiaawIcacaGL % Paaaaaa!3D25! D = \left( { - \infty ;2} \right)\)

Tập xác định D = R\{1}

Hoành độ giao điểm của đường thẳng d và đồ thị (C) là nghiệm của phương trình.

\( \frac{{x + 1}}{{x - 1}} = 2x -1\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuqr1ngBPrgarmqr1ngBPrgitL % xBI9gBamXvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2D % aeHbuLwBLnhiov2DGi1BTfMBaebbfv3ySLgzGueE0jxyaibaieYlf9 % irVeea0dXdh9vqqj-hEeeu0xXdbba9frFj0-OqFfea0dXdd9vqaq-J % frVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpWqaaeaabi % GaciaacaqabeaadaabauaaaOqaaiabgsDiBpaaceaaeaqabeaacqWG % 4baEcqGHGjsUcqaIXaqmaeaacqWG4baEdaahaaWcbeqaaiabikdaYa % aakiabgkHiTiabikdaYiabdIha4jabg2da9iabicdaWaaacaGL7baa % aaa!4E47! \Leftrightarrow \left\{ \begin{array}{l} x \ne 1\\ {x^2} - 2x = 0 \end{array} \right.\)\(\left[\begin{matrix}x = 0\\ x = 2\\ \end{matrix}\right.\)

Với x = 0 suy ra A ( 0 ; -1)

Với x = 2 suy ra B ( 2;3)

Do đó \(AB= { \sqrt{2^2+4^2} }= 2\sqrt{5}\)

Dựa vào bảng biến thiên ta thấy phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafa % Gaeyypa0JaaG4maiaadggacaWG4bWaaWbaaSqabeaacaaIYaaaaOGa % ey4kaSIaaGOmaiaadkgacaWG4bGaey4kaSIaam4yaiabg2da9iaaic % daaaa!42A3! y' = 3a{x^2} + 2bx + c = 0\) có hai nghiệm phân biệt đều dương.

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H49aai % qaaqaabeqaaiaadkgadaahaaWcbeqaaiaaikdaaaGccqGHsislcaaI % ZaGaamyyaiaadogacqGH+aGpcaaIWaaabaGaamiEamaaBaaaleaaca % aIXaaabeaakiabgUcaRiaadIhadaWgaaWcbaGaaGOmaaqabaGccqGH % 9aqpcqGHsisldaWcaaqaaiaaikdacaWGIbaabaGaaG4maiaadggaaa % GaeyOpa4JaaGimaaqaaiaadIhadaWgaaWcbaGaaGymaaqabaGccaGG % UaGaamiEamaaBaaaleaacaaIYaaabeaakiabg2da9maalaaabaGaam % 4yaaqaaiaadggaaaGaeyOpa4JaaGimaaaacaGL7baaaaa!5586! \Rightarrow \left\{ \begin{array}{l} {b^2} - 3ac > 0\\ {x_1} + {x_2} = - \frac{{2b}}{{3a}} > 0\\ {x_1}.{x_2} = \frac{c}{a} > 0 \end{array} \right.\) 

và hệ số a < 0 \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHRaWkcqGHEisP % aeqaaOWaaeWaaeaacaWGHbGaamiEamaaCaaaleqabaGaaG4maaaaki % abgUcaRiaadkgacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIa % am4yaiaadIhacqGHRaWkcaWGKbaacaGLOaGaayzkaaGaeyypa0Jaey % OeI0IaeyOhIukaaa!4E53! \mathop {\lim }\limits_{x \to + \infty } \left( {a{x^3} + b{x^2} + cx + d} \right) = - \infty \)

Từ đó suy ra c < 0 ; b > 0