Các góc tạo bởi một đường thẳng cắt hai đường thẳng
I. Các kiến thức cần nhớ
Cho hình vẽ
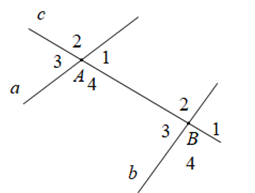
+ Hai cặp góc so le trong
\({\widehat A_4}\) và \({\widehat B_2}\); \({\widehat A_1}\) và \({\widehat B_3}\)
+ Bốn cặp góc đồng vị
\({\widehat A_2}\) và \({\widehat B_2}\); \({\widehat A_3}\) và \({\widehat B_3}\); \({\widehat A_4}\) và \({\widehat B_4}\); \({\widehat A_1}\) và \({\widehat B_1}\)
+ Hai cặp góc trong cùng phía
\({\widehat A_1}\) và \({\widehat B_2}\); \({\widehat A_4}\) và \({\widehat B_3}\)
Quan hệ giữa các cặp góc
Nếu hai đường thẳng cắt một đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
+ Hai góc so le trong còn lại bằng nhau
+ Hai góc đồng vị bằng nhau
+ Hai góc trong cùng phía bù nhau
Ví dụ: \({\widehat A_1} = {\widehat B_1} \Rightarrow \left\{ \begin{array}{l}{\widehat A_2} = {\widehat B_2}\\{\widehat A_3} = {\widehat B_1}\\{\widehat A_2} + {\widehat B_1} = {180^0}\end{array} \right.\)
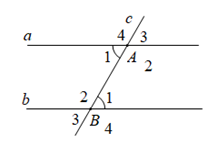
II. Các dạng toán thường gặp
Dạng 1: Xác định các cặp góc so le trong, cặp góc đồng vị, cặp góc trong cùng phía
Phương pháp:
Căn cứ vào vị trí của góc so với hai đường thẳng và đường thẳng thứ ba
Dạng 2: Tính số đo góc khi biết một trong bốn góc tạo bởi hai đường thẳng
Phương pháp:
Chú ý đến tính chất các góc đối đỉnh và các góc kề bù
Dạng 3: Tìm các cặp góc bằng nhau, cặp góc bù nhau
Phương pháp:
Sử dụng quan hệ giữa các cặp góc so le trong, cặp góc đồng vị và cặp góc trong cùng phía.
