Tính chất ba đường trung tuyến của tam giác
1. Các kiến thức cần nhớ
Nhắc lại: Đường trung tuyến của một tam giác là đoạn thẳng nối đỉnh và trung điểm cạnh đối diện.
Định lý 1: Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác đó.
Định lý 2: Vị trí trọng tâm: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.
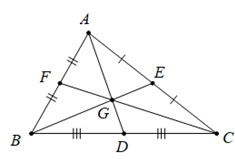
Ví dụ: Cho tam giác \(ABC\) có các đường trung tuyến \(AD,BE,CF\) cắt nhau tại \(G\). Khi đó $G$ là trọng tâm của \(\Delta ABC\) (hình vẽ), nên ta có
\(AG = \dfrac{2}{3}AD;\) \(BG = \dfrac{2}{3}BE;\) \(CG = \dfrac{2}{3}CF.\)
2. Các dạng toán thường gặp
Dạng 1: Tìm các tỉ lệ giữa các cạnh, tính độ dài đoạn thẳng
Phương pháp:
Chú ý đến vị trí trọng tâm của tam giác.
Với G là trọng tâm của \(\Delta ABC\) và \(AD,BE,CF\) là ba đường trung tuyến ta có
\(AG = \dfrac{2}{3}AD;\) \(BG = \dfrac{2}{3}BE;\) \(CG = \dfrac{2}{3}CF.\)
Dạng 2: Đường trung tuyến với các tam giác đặc biệt (tam giác cân, tam giác đều, tam giác vuông)
Phương pháp:
Chú ý rằng trong tam giác cân ( hoặc tam giác đều) đường trung tuyến ứng với cạnh đáy chia tam giác thành hai tam giác bằng nhau.
