Con lắc vướng đinh - sự trùng phùng của hai con lắc
I- ĐỘ CAO CON LẮC VƯỚNG ĐINH
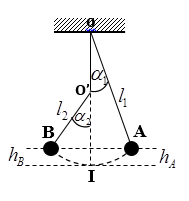
Phương pháp:
Một con lắc đơn đang dao động điều hòa với chiều dài ℓ1 thì con lắc vướng đinh làm cho nó dao động với ℓ2 nên chu kì, tần số góc, biên độ góc,… cũng thay đổi theo.
Chu kì T của CLVĐ:
\(T = \dfrac{1}{2}\left( {{T_1} + {T_2}} \right) \to T = \dfrac{\pi }{{\sqrt g }}(\sqrt {{l_1}} + \sqrt {{l_2}} )\)
Độ cao CLVĐ so với VTCB :
Vì \({W_A} = {W_B} \Rightarrow {h_A} = {\rm{ }}{h_B}\)
Tỉ số biên độ dao động 2 bên VTCB
– Góc lớn (α0>100):
Vì \(h_A = h_B\)
→ℓ1 (1–cosα1) = ℓ2(1–cosα2)
\( \to \dfrac{{{l_1}}}{{{l_2}}} = \dfrac{{1 - c{\rm{os}}{\alpha _2}}}{{1 - c{\rm{os}}{\alpha _1}}}\)
– Góc nhỏ:
$\left( {{\alpha _0} \le {\rm{ }}{{10}^0}) \to cos\alpha \approx 1-{\alpha ^2}/2} \right): \to \dfrac{{{l_1}}}{{{l_2}}} = {(\dfrac{{{\alpha _2}}}{{{\alpha _1}}})^2}$
II- SỰ TRÙNG PHÙNG CỦA HAI CON LẮC
Xét 2 con lắc dao động trong 2 mặt phẳng song song, con lắc 1 có chu kì T1, con lắc hai có chu kì T2 (T1>T2). Tại thời gian t = 0 hai con lắc có cùng 1 trạng thái (VD: cùng qua VTCB theochiều + chẳng hạn), sau thời gian nào đó trạng thái của 2 con lắc lại giống như trạng thái lúc t = 0 (tức lại cùng qua VTCB theo chiều +) được gọi là sự trùng phùng.
Phương pháp:
Thời gian ∆t nhỏ nhất kể từ khi thời điểm t = 0 cho tới lúc 2 còn lắc trùng phùng lần thứ nhất gọi là chu kì trùng phùng.
- Vì con lắc 2 có chu kì nhỏ hơn con lắc 1 nên sau lần dao động thứ nhất của con lắc 2 con lắc 1 cần 1 thời gian (T1-T2) để trở về vị trí xuất phát ban đầu của nó. Nói cách khác là con lắc 1 bị trễ so với con lắc 2 là (T1-T2).
- Sau n lần dao động của con lắc 2 khoảng thời gian trễ này sẽ là \(n.({T_1} - {T_2})\) . Để sự trùng phùng xảy ra thì khoảng thời gian trễ trên phải đúng bằng một chu kì T2. Hay:
\(\begin{array}{l}n({T_1} - {T_2}) = {T_2} \leftrightarrow n{T_1} = (n + 1){T_2} = \Delta t\\ \to \Delta \tau = \dfrac{{{T_1}{T_2}}}{{\left| {{T_1} - {T_2}} \right|}}\end{array}\)
hoặc \(\Delta t = b{T_1} = a{T_2}\) , trong đó: \(\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{a}{b}\) (phân số tối giản)
Thời gian trùng phùng lần đầu kể từ lúc t = 0 cũng chính là chu kì trùng phùng \(\Delta \tau \)
