Mẫu nguyên tử Bo - Quang phổ của nguyên tử Hidro
I - NỘI DUNG
1. Mẫu nguyên tử Bo
a. Tiên đề về trạng thái dừng
- Nguyên tử chỉ tồn tại trong những trạng thái có năng lượng xác định \({E_n}\) gọi là trạng thái dừng. Khi ở trạng thái dừng năng lượng không bức xạ.
- Bán kính quỹ dạo dừng: \({r_n} = {n^2}{r_0}\)
Trong đó:
- \({r_0}\) - bán kính nguyên tử ở trạng thái cơ bản \(\left( {{r_0} = {\rm{ }}{{5,3.10}^{ - 11}}} \right)\)
- \(n{\rm{ }} = {\rm{ }}1,{\rm{ }}2,{\rm{ }}3{\rm{ }}...\)

- Năng lượng electron trong nguyên tử hiđro: \({E_n} = - \dfrac{{13,6}}{{{n^2}}}eV\) với \(n \in N*\)
b. Tiên đề về sự bức xạ và hấp thụ
- Khi nguyên tử chuyển từ trạng thái dừng có năng lượng \({E_n}\) sang trạng thái có năng lượng \({E_m} < {\rm{ }}{E_n}\) thì nó phát ra một photon có năng lượng \(\varepsilon = {E_n} - {E_m}\).
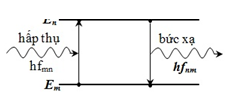
- Ngược lại, nếu nguyên tử ở trạng thái dừng có năng lượng \({E_m}\) mà hấp thụ được một phôtôn có năng lượng hf đúng bằng hiệu \({E_n}--{\rm{ }}{E_m}\) thì nó chuyển sang trạng thái dừng có năng lượng \({E_n}\) lớn hơn.
- Sự chuyển từ trạng thái dừng \({E_m}\) sang trạng thái dừng \({E_n}\) ứng với sự nhảy của electron từ quỹ đạo dừng có bán kính \({r_m}\) sang quỹ đạo dừng có bán kính \({r_n}\) và ngược lại.
2. Quang phổ vạch của nguyên tử Hidrro
- Bình thường electron (e) chỉ chuyển động trên quỹ đạo K (trạng thái cơ bản)
- Khi bị kích thích, e nhảy lên quỹ đạo có năng lượng lớn hơn L, M, N, ... Thời gian ở trạng thái kích thích rất ngắn (10-8s) sau đó e chuyển về các quỹ đạo bên trong và phát ra photon có năng lượng đúng bằng hiệu \(\varepsilon = {E_{cao}} - {E_{thap}}\)
- Mỗi photon tần số f ứng với vạch sáng có bước sóng \(\lambda = \dfrac{c}{f}\) cho 1 vạch quang phổ.
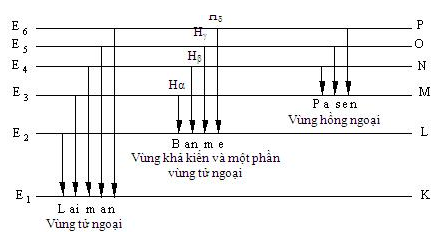
- Quang phổ vạch phát xạ của Hiđro nằm trong 3 dãy (hình trên)
- Dãy Laiman: e chuyển từ trạng thái kích thích \( \to \) quỹ đạo K
- Dãy Banme: e chuyển từ trạng thái kích thích \( \to \) quỹ đạo L
- Dãy Pasen: e chuyển từ trạng thái kích thích \( \to \) quỹ đạo M
Trong dãy Banme, nguyên tử Hiđro có 4 vạch: \({H_\alpha }\) (đỏ), \({H_\beta }\) (lam), \({H_\gamma }\) (chàm), \({H_\delta }\) (tím)
Ở trạng thái cơ bản \({E_1} = {\rm{ }} - 13,6eV,{E_n} = \dfrac{{{E_1}}}{{{n^2}}}\)
II - CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
1. Dạng 1: xác định vận tốc, tần số \(f\) , tốc độ góc \(\omega \) năng lượng của e ở trạng thái dừng thứ n.
Khi e chuyển động trên quỹ đạo n, lực hút tĩnh điện đóng vai trò là lực hướng tâm:
\(\left\{ \begin{array}{l}{F_{ht}} = {F_{CL}} \leftrightarrow \dfrac{{mv_n^2}}{{{r_n}}} = \dfrac{{k{q_1}{q_2}}}{{{r^2}}} = \dfrac{{k{e^2}}}{{{r_n}^2}}\\{r_n} = {n^2}{r_0}\end{array} \right. \to {v_n} = e\sqrt {\dfrac{k}{{{r_n}m}}} = \dfrac{e}{n}\sqrt {\dfrac{k}{{{r_0}m}}} \) với \(k{\rm{ }} = {\rm{ }}{9.10^9}\)
Tần số: \(f = \dfrac{\omega }{{2\pi }} = \dfrac{{{v_n}}}{{2\pi {r_n}}}\)
Năng lượng ở trạng thái dừng bao gồm: thế năng tương tác và động năng của electron:
\(\begin{array}{l}{E_n} = {{\rm{W}}_t} + {{\rm{W}}_{\rm{d}}} = - \dfrac{{k{e^2}}}{{{r_n}}} + \dfrac{{mv_n^2}}{2} = - mv_n^2 + \dfrac{{mv_n^2}}{2} = - \dfrac{{mv_n^2}}{2}\\ \to {v_n} = \sqrt { - \dfrac{{2{E_n}}}{m}} \end{array}\)
Khi e quay trên quỹ dạo dừng thì nó tạo ra dòng điện có cường độ: \(I = \dfrac{q}{t} = \dfrac{{\left| e \right|}}{T}\)
2. Dạng 2: tính bước sóng, tần số của photon hấp thụ hoặc bức xạ và số vạch quang phổ phát ra
\(\varepsilon = hf = \dfrac{{hc}}{\lambda } = {\rm{ }}{E_{cao}} - {\rm{ }}{E_{thap}}\)
Dựa vào sơ đồ mức năng lượng, ta có: \({E_3} - {\rm{ }}{E_1} = {\rm{ }}{E_3} - {\rm{ }}{E_2} + {\rm{ }}{E_2} - {\rm{ }}{E_1}\)
\({f_{31}} = {f_{32}} + {f_{21}} \to \dfrac{1}{{{\lambda _{31}}}} = \dfrac{1}{{{\lambda _{32}}}} + \dfrac{1}{{{\lambda _{21}}}}\)
\({f_{41}} = {f_{43}} + {f_{32}} + {f_{21}} \to \dfrac{1}{{{\lambda _{43}}}} + \dfrac{1}{{{\lambda _{32}}}} + \dfrac{1}{{{\lambda _{21}}}}\)
Số vạch quang phổ phát ra tối đa của một khối khí: \(\dfrac{{n(n - 1)}}{2}\)
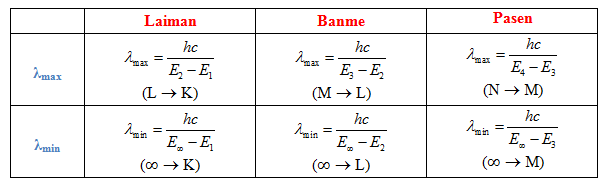
3. Dạng 3: tính \({\lambda _{{\bf{max}}}},{\lambda _{{\bf{min}}}}\) trong các dãy.
\(\dfrac{{hc}}{\lambda } = {\rm{ }}{E_n} - {\rm{ }}{E_m} \to \lambda = \dfrac{{hc}}{{{E_n} - {\rm{ }}{E_m}}}\); \({E_\infty } = {\rm{ }}0\)