Phương pháp giải bài tập sóng cơ - Các đại lượng đặc trưng cơ bản của sóng cơ học

Phương pháp giải bài tập sóng cơ - các đại lượng đặc trưng cơ bản của sóng cơ học MÔN LÝ Lớp 12 với nhiều phương pháp giải nhanh kèm bài tập vận dụng
(442) 1474 26/07/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    I. Bảng tóm tắt các đại lượng đặc trưng của sóng cơ

    II. Phương pháp giải bài tập sóng cơ - Các đại lượng đặc trưng cơ bản của sóng cơ học

    DẠNG  BÀI: TÌM CHU KỲ, TẦN SỐ, BƯỚC SÓNG, ĐỘ LỆCH PHA GIỮ HAI ĐIỂM TRÊN PHƯƠNG TRUYỀN

    Phương pháp:

    - Chu kỳ \(\left( T \right)\) , vận tốc \(\left( v \right)\) , tần số \(\left( f \right)\) , bước sóng \((\lambda )\) liên hệ với nhau :

    \(f = \frac{1}{T};\lambda  = vT = \frac{v}{f};v = \frac{{\Delta s}}{{\Delta t}}\) với \(\Delta s\)  là quãng đường sóng truyền trong thời gian \(\Delta t\).

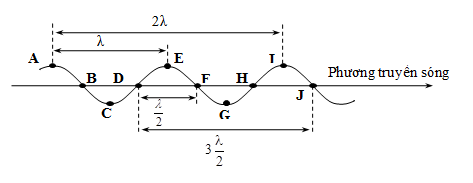
    - Quan sát hình ảnh sóng có n ngọn sóng liên tiếp thì có n - 1 bước sóng. Hoặc quan sát thấy từ ngọn sóng thứ n đến ngọn sóng thứ m (m > n) có chiều dài l thì bước sóng: \(\lambda  = \frac{l}{{m - n}}\)

    - Số lần nhô lên trên mặt nước là N trong khoảng thời gian t giây thì \(T = \frac{t}{{N - 1}}\)

    - Độ lệch pha giữa hai điểm cách nguồn một khoảng xM, xN:

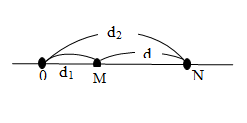
    \(\Delta {\varphi _{MN}} = \omega \frac{{{x_N} - {x_M}}}{v} = 2\pi \frac{{{x_N} - {x_M}}}{\lambda } = 2\pi \frac{d}{\lambda }\)  trong đó: \({x_N} - {x_M} = d\)  

    • Nếu 2 điểm M và N dao động cùng pha thì:

    \(\Delta {\varphi _{MN}} = 2k\pi  <  =  > 2\pi \frac{d}{\lambda } = 2k\pi  <  =  > d = k\lambda \).      \(({\rm{ }}k \in Z{\rm{ }})\)

    • Nếu 2 điểm M và N dao động ngược pha thì:

    \(\Delta {\varphi _{MN}} = (2k + 1)\pi  <  =  > 2\pi \frac{d}{\lambda } = (2k + 1)\pi  <  =  > d = (2k + 1)\frac{\lambda }{2}\).  \(({\rm{ }}k \in Z{\rm{ }})\)

    • Nếu 2 điểm M và N dao động vuông pha thì:

    \(\Delta {\varphi _{MN}} = (2k + 1)\frac{\pi }{2} <  =  > 2\pi \frac{d}{\lambda } = (2k + 1)\frac{\pi }{2} <  =  > d = (2k + 1)\frac{\lambda }{4}\). \(({\rm{ }}k \in Z{\rm{ }})\)

    Đơn vị của \(x,{\rm{ }}{x_1},{\rm{ }}{x_2},d,\lambda ,v\) phải tương ứng với nhau.

    Xem toàn bộ nội dung Vật lý 12:

    (442) 1474 26/07/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý Thuyết Lớp 12 Vật lý 12