Ôn tập chương 2 - Sóng cơ và sóng âm

I. Bảng tổng hợp lý thuyết chương 2: Sóng cơ

II. Ôn tập chương 2 - Sóng cơ và sóng âm

I – SỰ TRUYỀN SÓNG CƠ

1. Định nghĩa

Sóng ngang truyền được trong chất rắn và bề mặt chất lỏng

Ví dụ: Sóng trên mặt nước, sóng trên sợi dây cao su

Sóng dọc truyền được cả trong chất rắn, lỏng và khí.

Ví dụ: sóng âm, sóng trên một lò xo

2. Phương trình sóng

Phương trình tại nguồn: \({u_0} = Ac{\rm{os}}\omega {\rm{t}}\)

Phương trình sóng tại một điểm M trên phương truyền sóng Ox là: \(u = Acos\left( {\omega t + \varphi  \pm \dfrac{{2\pi d}}{\lambda }} \right)\)

+ Nếu M ở trước O theo chiều truyền sóng thì ${\varphi _M} = \varphi  + {\text{ }}2\pi \dfrac{x}{\lambda }$

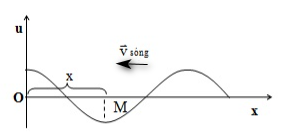
+ Nếu M ở sau O theo chiều truyền sóng thì ${\varphi _M} = \varphi  - {\rm{ }}2\pi \dfrac{x}{\lambda }$

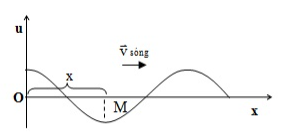
3. Độ lệch pha

Độ lệch pha \(\Delta \varphi  = \dfrac{{2\pi d}}{\lambda }\) , trong đó $d$- khoảng cách hai điểm

+ Hai điểm dao động cùng pha nếu: \(\Delta \varphi  = k2\pi \)  hay \(d = k\lambda \)

+ Hai điểm dao động ngược pha nếu: \(\Delta \varphi  = \left( {2k + 1} \right)\pi \) hay \(d = \left( {2k + 1} \right)\dfrac{\lambda }{2}\)

+ Hai điểm dao động vuông pha nếu: \(\Delta \varphi  = \left( {2k + 1} \right)\dfrac{\pi }{2}\) hay \(d = \left( {2k + 1} \right)\dfrac{\lambda }{4}\)

II – GIAO THOA SÓNG

* Điều kiện giao thoa: Hai sóng là hai sóng kết hợp tức là hai sóng cùng tần số và có độ lệch pha không đổi theo thời gian.

Xét với hai nguồn cùng pha, ta có:

+ Biên độ dao động tổng hợp tại M: \({A_M} = \left| {2acos\left( {\dfrac{{\pi \left( {{d_1} - {d_2}} \right)}}{\lambda }} \right)} \right|\)

+ Điểm có biên độ cực đại khi: \(\Delta d = {d_1} - {d_2} = k\lambda \)

+ Điểm có biên độ cực tiểu khi: \(\Delta d = {d_1} - {d_2} = \left( {2k + 1} \right)\dfrac{\lambda }{2}\)

+ Số điểm dao động cực đại, cực tiểu giữa hai nguồn AB (không tính hai nguồn)

* Số Cực đại: $ - \dfrac{l}{\lambda }  < k <  + \dfrac{l}{\lambda } $

* Số Cực tiểu: $ - \dfrac{l}{\lambda } - \dfrac{1}{2} < k <  + \dfrac{l}{\lambda } - \dfrac{1}{2}{\rm{     (k}} \in {\rm{Z)}}$    Hay  $ - \dfrac{l}{\lambda } < k + 0,5 <  + \dfrac{l}{\lambda }{\rm{     (k}} \in {\rm{Z)}}$

Xem đầy đủ các dạng bài giao thoa sóng cơ

Xem các dạng bài về pha dao động

III – SÓNG DỪNG

Trong sóng dừng có một số điểm luôn luôn đứng yên gọi là nút, và một số điểm luôn luôn dao động với biên độ cực đại gọi là bụng.

+ Khoảng cách giữa 2 nút hoặc 2 bụng liền kề của sóng dừng là \(\dfrac{\lambda }{2}\).

+ Khoảng cách giữa nút và bụng liền kề là \(\dfrac{\lambda }{4}\) .

+ Khoảng cách giữa hai nút (bụng, múi) sóng bất kỳ là : \(k\dfrac{\lambda }{2}\)

- Phương trình sóng dừng nếu chọn góc O là nút:

\(u = {A_b}\sin \dfrac{{2\pi x}}{\lambda }cos\left( {\omega t + \varphi } \right)\)

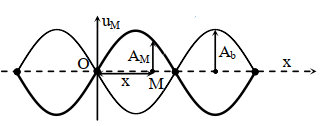
- Điều kiện xảy ra sóng dừng:

IV – SÓNG ÂM

- Các đặc trưng vật lí của âm:

+ Tần số \(f\)

+ Cường độ âm: \(I = \dfrac{{\rm{W}}}{{St}} = \dfrac{P}{S} = \dfrac{P}{{4\pi {r^2}}}\)

+ Mức cường độ âm: \(L = \log \dfrac{I}{{{I_0}}}\left( B \right) = 10\log \dfrac{I}{{{I_0}}}\left( {dB} \right)\)

- Các đặc trứng sinh lí của âm                                                  

+ Độ cao: là một đặc trưng sinh lí phụ thuộc vào tần số âm, không phụ thuộc vào năng lượng âm.

+ Độ to: là 1 đặc trưng sinh lí phụ thuộc vào tần số âm và mức cường độ âm.

+ Âm sắc: là đặc trưng của âm giúp ta phân biệt được các âm phát ra từ các nguồn khác nhau. Âm sắc liên quan đến đồ thị dao động âm.