Phương pháp giải bài tập sự thay đổi chu kì con lắc đơn khi chịu thêm tác dụng của lực lạ
Chu kì dao động của con lắc đơn khi con lắc chịu thêm tác dụng của lực lạ là: \(T' = 2\pi \sqrt {\frac{l}{{g'}}} \)
Ta có: \(\overrightarrow {P'} = \overrightarrow P + \overrightarrow F \)
Trong đó: \(\overrightarrow {P'} \) : trọng lực biểu kiến (có vai trò như trọng lực), \(\overrightarrow P \) : trọng lực, \(\overrightarrow F \) lực lạ.
\( \to \overrightarrow {g'} = \overrightarrow g + \frac{{\overrightarrow F }}{m}\) : gia tốc trọng trường hiệu dụng hay gia tốc trọng trường biểu kiến.
I- CÁC LỰC LẠ THƯỜNG GẶP:
- Lực quán tính: \(\overrightarrow F = - m\overrightarrow a \), độ lớn F = ma ( \(\overrightarrow F \uparrow \downarrow \overrightarrow a \))
+ Chuyển động nhanh dần đều \(\overrightarrow a \uparrow \uparrow \overrightarrow v \) (\(\overrightarrow v \) có hướng chuyển động)
+ Chuyển động chậm dần đều \(\overrightarrow a \uparrow \downarrow \overrightarrow v \)
- Lực điện trường: \(\overrightarrow F = q\overrightarrow E \), độ lớn F = |q|E (Nếu q > 0 Þ \(\overrightarrow F \uparrow \uparrow \overrightarrow E \); còn nếu q < 0 Þ \(\overrightarrow F \uparrow \downarrow \overrightarrow E \))
- Lực đẩy Ácsimét: \(F = DgV\) (\(\overrightarrow F \)luông thẳng đứng hướng lên)
Trong đó:
- D là khối lượng riêng của chất lỏng hay chất khí.
- g là gia tốc rơi tự do.
- V là thể tích của phần vật chìm trong chất lỏng hay chất khí đó.
II- CÔNG THỨC ÁP DỤNG LÀM BÀI TẬP
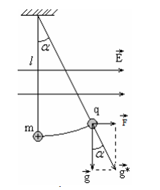
- \(\overrightarrow F \) có phương ngang: \(\overrightarrow F \bot \overrightarrow P \)
Tại VTCB dây treo lệch với phương thẳng đứng một góc có: \(\tan \alpha = \frac{F}{P}\)
Thì \(g' = \sqrt {{g^2} + {{(\frac{F}{m})}^2}} \)
Ví dụ:
- \(\overrightarrow F \)có phương thẳng đứng thì \(g' = g \pm \frac{F}{m}\)
- Nếu \(\overrightarrow F \) hướng xuống thì \(g' = g + \frac{F}{m}\)
- Nếu \(\overrightarrow F \) hướng lên thì \(g' = g - \frac{F}{m}\)
- \(\overrightarrow F \)có hướng xiên:
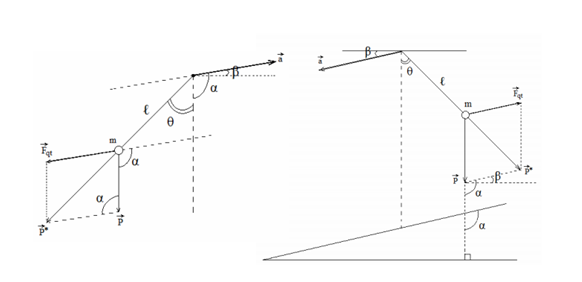
- Xiên xuống:
\(\begin{array}{l}P' = \sqrt {{P^2} + F_{qt}^2 - 2P.{F_{qt}}{\rm{cos}}\left( {{{90}^0} + \beta } \right)} \\ \to g' = \sqrt {{g^2} + {a^2} - 2g.ac{\rm{os(9}}{{\rm{0}}^0} + \beta )} \end{array}\)
Góc θ: \(\frac{a}{{\sin \theta }} = \frac{{g'}}{{\sin ({{90}^0} + \beta )}}\)
- Xiên lên:
\(\begin{array}{l}P' = \sqrt {{P^2} + F_{qt}^2 - 2P.{F_{qt}}{\rm{cos}}\left( {{{90}^0} - \beta } \right)} \\ \to g' = \sqrt {{g^2} + {a^2} - 2g.ac{\rm{os(9}}{{\rm{0}}^0} - \beta )} \end{array}\)
Vì \(cos(\pi - a) = - cosa\)
\( \to P' = \sqrt {{P^2} + F_{qt}^2 + 2P.{F_{qt}}{\rm{cos}}\alpha } \)
Góc θ: \(\frac{a}{{\sin \theta }} = \frac{{g'}}{{\sin ({{90}^0} - \beta )}}\)
