Mạch dao động LC - Các đại lượng đặc trưng
I - NỘI DUNG LÍ THUYẾT
1. Mạch dao động điện từ tự do
- Mạch dao động LC bao gồm một tụ điện có điện dung C và cuộn cảm có độ tự cảm L tạo thành mạch kín, gọi là mạch dao động hay khung dao động.
- Điện tích trên tụ điện dao động điều hòa với tần số góc ω có biểu thức: \(q{\rm{ }} = {\rm{ }}{Q_0}cos\left( {\omega t + \varphi } \right)\)
- Dòng điện tức thời qua cuộn cảm có biểu thức: \(i = q' = - \omega {Q_0}sin(\omega t + \varphi ) = {I_0}cos(\omega t + \varphi + \dfrac{\pi }{2})\)
- Điện áp giữa hai đầu tụ điện có biểu thức: \(u = \dfrac{q}{C} = \dfrac{{{Q_0}}}{C}{\rm{cos(}}\omega {\rm{t + }}\varphi {\rm{) = }}{{\rm{U}}_0}{\rm{cos(}}\omega {\rm{t + }}\varphi {\rm{)}}\)
- Các đại lượng đặc trưng riêng cho mạch dao động LC:
\(\omega = \dfrac{1}{{\sqrt {LC} }},{\rm{ }}f = \dfrac{1}{{2\pi \sqrt {LC} }},{\rm{ }}T = 2\pi \sqrt {LC} \)
- Mối liên hệ giữa các giá trị cực đại:
\({I_0} = \omega {Q_0} = \dfrac{{{Q_0}}}{{\sqrt {LC} }}\) , \({U_0} = \dfrac{{{Q_0}}}{C} = \dfrac{{{I_0}}}{{\omega C}} = \omega L{I_0} = {I_0}\sqrt {\dfrac{L}{C}} \)
- Biến thiên của điện và từ trường trong mạch LC được gọi là dao động điện từ. Nếu không có tác động về điện hoặc từ với bên ngoài thì được gọi là dao động điện từ tự do.
2. Năng lượng điện từ trong mạch dao động
- Năng lượng điện trường tập trung ở trong tụ điện: \({W_d} = \dfrac{1}{2}C{u^2} = \dfrac{1}{2}qu = \dfrac{{{q^2}}}{{2C}} = \dfrac{{Q_0^2}}{{2C}}{\rm{co}}{{\rm{s}}^2}(\omega t + \varphi )\)
- Năng lượng từ trường tập trung trong cuộn cảm: \({W_t} = \dfrac{1}{2}L{i^2} = \dfrac{{Q_0^2}}{{2C}}{\sin ^2}\left( {\omega t + \varphi } \right)\)
- Trong quá trình dao động của mạch, năng lượng từ và năng lượng điện trường luôn chuyển hóa cho nhau, nhưng tổng năng lượng điện từ là không đổi.
- Mạch dao động có tần số góc \(\omega \) , tần số f và chu kì T thì Wđ và Wt biến thiên với tần số góc \(2\omega \) , tần số \(2f\) và chu kì T/2.
- Khi tụ phóng điện thì q và u giảm và ngược lại khi tụ tích điện thì q và u tăng.
II - CÁC DẠNG BÀI TẬP
1. Dạng 1: Xác định chu kì, tần số của mạch dao động
- Tần số góc: \(\omega = \dfrac{1}{{\sqrt {LC} }}{\rm{ }} \to T = 2\pi \sqrt {LC} ;{\rm{ }}f = \dfrac{1}{{2\pi \sqrt {LC} }}\)
- Lập tỉ số, ta có: \(\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{{f_2}}}{{{f_1}}} = \dfrac{{{\omega _1}}}{{{\omega _2}}} = \sqrt {\dfrac{{{L_2}}}{{{L_1}}}} .\sqrt {\dfrac{{{C_2}}}{{{C_1}}}} \)
- \({\omega _0} = \dfrac{1}{{\sqrt {LC} }} = \dfrac{{{I_0}}}{{{Q_0}}},{\rm{ }} \to {\rm{T = 2}}\pi \dfrac{{{Q_0}}}{{{I_0}}},{\rm{ f = }}\dfrac{{{I_0}}}{{2\pi {Q_0}}}\)
- Bài toán ghép tụ điện nối tiếp và song song
Mạch gồm L và C1 có tần số f1 - Mạch gồm L và C2 có tần số f2
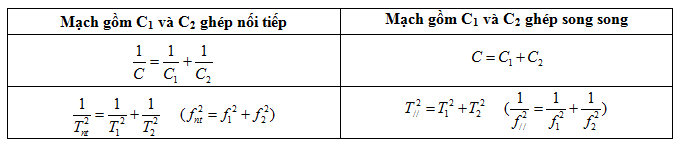
- Bài toán ghép cuộn cảm nối tiếp và song song
Mạch gồm L1 và C có tần số f1 - Mạch gồm L2 và C có tần số f2
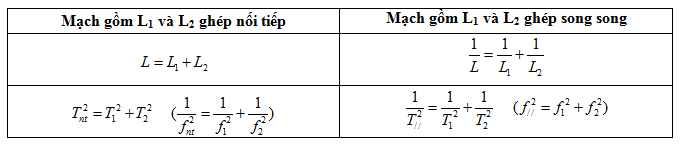
2. Dạng 2: Xác định I0, Q0, U0, u, i
- Từ phương trình dao động: \(q = {Q_0}cos\left( {\omega t + \varphi } \right),i = q' = - \omega {Q_0}sin(\omega t + \varphi ) = {I_0}cos(\omega t + \varphi + \dfrac{\pi }{2})\)
\(u = \dfrac{q}{C} = \dfrac{{{Q_0}}}{C}{\rm{cos(}}\omega {\rm{t + }}\varphi {\rm{) = }}{{\rm{U}}_0}{\rm{cos(}}\omega {\rm{t + }}\varphi {\rm{)}}\)
=> Mối liên hệ giữa các đại lượng:
\({I_0} = \omega {Q_0} = \dfrac{{{Q_0}}}{{\sqrt {LC} }}\) , \({U_0} = \dfrac{{{Q_0}}}{C} = \dfrac{{{I_0}}}{{\omega C}} = \omega L{I_0} = {I_0}\sqrt {\dfrac{L}{C}} \)
- Điện áp tức thời:
- Cách 1: Thay vào phương trình: \(u = \dfrac{q}{C} = \dfrac{{{Q_0}}}{C}{\rm{cos(}}\omega {\rm{t + }}\varphi {\rm{) = }}{{\rm{U}}_0}{\rm{cos(}}\omega {\rm{t + }}\varphi {\rm{)}}\)
- Cách 2: \({u^2} = U_0^2 - \dfrac{L}{C}{i^2} = \dfrac{L}{C}(I_0^2 - {i^2})\)
- Dòng điện tức thời:
- Cách 1: Thay vào phương trình:\(i = q = - \omega {Q_0}sin(\omega t + \varphi ) = {I_0}cos(\omega t + \varphi + \dfrac{\pi }{2})\)
- Cách 2: \({i^2} = I_0^2 - \dfrac{C}{L}{u^2} = \dfrac{C}{L}(U_0^2 - {u^2})\)
- Điện tích tức thời:
- Cách 1: Thay vào phương trình: \(q = {Q_0}cos\left( {\omega t + \varphi } \right)\)
- Cách 2: \({q^2} = {(Cu)^2} = Q_0^2 - \dfrac{{{i^2}}}{{{\omega ^2}}} = \dfrac{1}{{{\omega ^2}}}(I_0^2 - {i^2})\)
Điện áp và cường độ dòng điện hiệu dụng: \(U = \dfrac{{{U_0}}}{{\sqrt 2 }};I = \dfrac{{{I_0}}}{{\sqrt 2 }}\)
