Đề thi thử THPT QG năm 2022 môn Toán - Trường THPT Tiên Lãng
Đề thi thử THPT QG năm 2022 môn Toán
-
Hocon247
-
50 câu hỏi
-
90 phút
-
62 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Nếu \(\int {f\left( x \right)} dx = \dfrac{{{x^3}}}{3} + {e^x} + C\) thì \(f\left( x \right)\) bằng
\(\int {f\left( x \right)} dx = \dfrac{{{x^3}}}{3} + {e^x} + C \Rightarrow f\left( x \right) = {x^2} + {e^x}\).
Chọn: C
Có bao nhiêu giá trị x thỏa mãn \({5^{{x^2}}} = {5^x}\)?
Ta có: \({5^{{x^2}}} = {5^x} \Leftrightarrow {x^2} = x \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\).
Chọn: D
Đường cong trong hình bên là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Quan sát đồ thị ta thấy: Đồ thị hàm số đi qua điểm \(O\left( {0;0} \right)\).
Chọn: B
Với giá trị nào của x thì biểu thức \({\left( {4 - {x^2}} \right)^{\frac{1}{3}}}\) sau có nghĩa
ĐKXĐ: \(4 - {x^2} > 0 \Leftrightarrow - 2 < x < 2\).
Chọn: C
Đường cong trong hình bên là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Hàm số đồng biến trên \(\left( {0; + \infty } \right) \Rightarrow \)Loại phương án C
Đồ thị hàm số đi qua điểm \(\left( {\dfrac{1}{2}; - 1} \right) \Rightarrow \) Chọn phương án B , do \( - 1 \ne {\log _2}\left( {2.\dfrac{1}{2}} \right);\,\,\,\, - 1 = {\log _2}\dfrac{1}{2}\) và \( - 1 \ne {\log _{\sqrt 2 }}\dfrac{1}{2}\)
Chọn: B
Có bao nhiêu điểm thuộc đồ thị \(\left( C \right)\) của hàm số \(y = \dfrac{2}{{{x^2} + 2x + 2}}\) có hoành độ và tung độ đều là số nguyên?
Ta có: \(y = \dfrac{2}{{{x^2} + 2x + 2}} = \dfrac{2}{{{{\left( {x + 1} \right)}^2} + 1}}\)
Mà \(0 < \dfrac{2}{{{{\left( {x + 1} \right)}^2} + 1}} \le 2,\,\,do{\left( {x + 1} \right)^2} \ge 0 \Rightarrow y \in \left\{ {1;2} \right\}\)
Với \(y = 1 \Rightarrow \dfrac{2}{{{x^2} + 2x + 2}} = 1 \Leftrightarrow {x^2} + 2x + 2 = 2 \Leftrightarrow {x^2} + 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right. \Rightarrow \) Các điểm \(\left( { - 2;1} \right),\,\,\left( {0;1} \right)\) thỏa mãn.
Với \(y = 2 \Rightarrow \dfrac{2}{{{x^2} + 2x + 2}} = 2 \Leftrightarrow {x^2} + 2x + 2 = 1 \Leftrightarrow {x^2} + 2x + 1 = 0 \Leftrightarrow x = - 1 \Rightarrow \) Điểm \(\left( { - 1;2} \right)\) thỏa mãn.
Vậy, đồ thị \(\left( C \right)\) có 3 điểm có hoành độ và tung độ đều là số nguyên.
Chọn: D
Xét một bảng ô vuông gồm \(4 \times 4\) ô vuông. Người ta điền vào mỗi ô vuông một trong hai số 1 hoặc -1 sao cho tổng các số trong mỗi hàng và tổng các số trong mỗi cột đều bằng 0. Hỏi có bao nhiêu cách điền số?
Nhận xét:
Để tổng các số trong mỗi hàng và tổng các số trong mỗi cột đều bằng 0 thì số lượng số 1 và số lượng số -1 trong mỗi hàng và mỗi cột đều là 2.
\( \Leftrightarrow \) Mỗi hàng và mỗi cột đều có đúng 2 số 1.
- Chọn 2 ô ở cột 1 để đặt số 1, ta có: \(C_4^2 = 6\) (cách)
Ví dụ:
- Ở mỗi hàng mà chứa 2 ô vừa được chọn, ta chọn đúng 1 ô để đặt số 1, khi đó có 2 trường hợp:
TH1: 2 ô được chọn ở cùng một hàng: có \(C_3^1 = 3\) (cách)
Ví dụ:
Khi đó, ở 2 hàng còn lại có duy nhất cách đặt số 1 vào 4 ô : không cùng hàng và cột với các ô đã điền.
Như hình vẽ sau:
TH2: 2 ô được chọn khác hàng: có: \(3.2 = 6\) (cách)
Ví dụ:
Khi đó, số cách đặt 4 số 1 còn lại là: \(1.1.2! = 2\) (cách), trong đó, 2 số 1 để vào đúng 2 ô còn lại của cột chưa điền, 2 số 1 còn lại hoàn vị vào 2 ô ở 2 cột vừa điền ở bước trước.
Ví dụ:
Vậy, số cách xếp là: \(6.\left( {3.1 + 6.2} \right) = 6.15 = 90\) (cách).
Chọn: B
Hỏi có bao nhiêu giá trị m nguyên trong \(\left[ { - 2017;2017} \right]\) để phương trình \(\log \left( {mx} \right) = 2\log \left( {x + 1} \right)\) có nghiệm duy nhất?
\(\log \left( {mx} \right) = 2\log \left( {x + 1} \right) \Leftrightarrow \left\{ \begin{array}{l}x > - 1\\mx = {\left( {x + 1} \right)^2}\end{array} \right.\) (I)
Ta thấy \(x = 0\) không phải nghiệm của, khi đó \((I) \Leftrightarrow \) \(\left\{ \begin{array}{l}x > - 1\\m = \dfrac{{{{\left( {x + 1} \right)}^2}}}{x} = x + \dfrac{1}{x} + 2\end{array} \right.\) (II)
Xét hàm số \(f\left( x \right) = x + \dfrac{1}{x} + 2,\,\,\,x \in \left( { - 1; + \infty } \right){\rm{\backslash }}\left\{ 0 \right\}\) có \(f'\left( x \right) = 1 - \dfrac{1}{{{x^2}}}\)
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1(L)\end{array} \right.\)
Bảng biến thiên:
Dựa vào bảng biên thiên, ta có: phương trình đã cho có 1 nghiệm duy nhất \( \Leftrightarrow \left[ \begin{array}{l}m < 0\\m = 4\end{array} \right.\)
Mà \(m \in \mathbb{Z},\,\,m \in \left[ { - 2017;2017} \right] \Rightarrow m \in \left\{ { - 2017; - 2016;...; - 1} \right\} \cup \left\{ 4 \right\}\): Có 2018 giá trị của m thỏa mãn.
Chọn: D
Đạo hàm của hàm số \(y = \sin \,x + {\log _3}{x^3}\,\,\left( {x > 0} \right)\) là
\(y = \sin \,x + {\log _3}{x^3}\,\, = \sin \,x + 3{\log _3}x\,\,\left( {x > 0} \right)\,\,\, \Rightarrow y' = \cos x + \dfrac{3}{{x\ln 3}}\).
Chọn: A
Nguyên hàm của hàm số \(f\left( x \right) = {x^{2019}}\), \(\left( {x \in \mathbb{R}} \right)\) là hàm số nào trong các hàm số dưới đây?
\(\int {f\left( x \right)dx} = \int {{x^{2019}}} dx = \dfrac{{{x^{2020}}}}{{2020}} + C\).
Chọn: C
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm O cạnh a, SO vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SO = a\). Khoảng cách giữa \(SC\) và \(AB\) bằng
Ta có: \(\left\{ \begin{array}{l}AB//CD\\CD \subset \left( {SCD} \right)\\AB \not\subset \left( {SCD} \right)\end{array} \right.\,\, \Rightarrow AB//\left( {SCD} \right)\,\).
Mà \(SC \subset \left( {SCD} \right)\,\, \Rightarrow d\left( {AB;SC} \right) = d\left( {AB;\left( {SCD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right)\)
Do \(O\) là trung điểm của AC,
\( \Rightarrow \dfrac{{d\left( {A;\left( {SCD} \right)} \right)}}{{d\left( {O;\left( {SCD} \right)} \right)}} = \dfrac{{AC}}{{OC}} = 2 \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = 2d\left( {O;\left( {SCD} \right)} \right)\)
Gọi I là trung điểm của CD. Dựng \(OH \bot SI,\,\,H \in SI\) (1)
Ta có: \(\left\{ \begin{array}{l}CD \bot OI\\CD \bot SO\end{array} \right.\,\, \Rightarrow CD \bot \left( {SOI} \right) \Rightarrow CD \bot OH\) (2)
Từ (1), (2), suy ra \(OH \bot \left( {SCD} \right)\, \Rightarrow d\left( {O;\left( {SCD} \right)} \right) = OH\)
\(\Delta SOI\)vuông tại O, \(OH \bot SI \Rightarrow \dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{I^2}}} + \dfrac{1}{{S{O^2}}} = \dfrac{1}{{{{\left( {\dfrac{a}{2}} \right)}^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{5}{{{a^2}}} \Rightarrow OH = \dfrac{{a\sqrt 5 }}{5}\)
\( \Rightarrow d\left( {AB;CD} \right) = \dfrac{{2a\sqrt 5 }}{5}\).
Chọn: C
Trong không gian với hệ tọa độ \(Oxyz\), cho \(A\left( { - 3;0;0} \right),\,B\left( {0;0;3} \right),C\left( {0; - 3;0} \right)\). Điểm \(M\left( {a;b;c} \right)\) nằm trên mặt phẳng \(Oxy\) sao cho \(M{A^2} + M{B^2} - M{C^2}\) nhỏ nhất. Tính \({a^2} + {b^2} - {c^2}\).
\(A\left( { - 3;0;0} \right),\,B\left( {0;0;3} \right),C\left( {0; - 3;0} \right)\)
+) Xác định điểm \(I\) thỏa mãn \(\overrightarrow {IA} + \overrightarrow {IB} - \overrightarrow {IC} = \overrightarrow 0 \):
\(\overrightarrow {IA} + \overrightarrow {IB} - \overrightarrow {IC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {IA} = \overrightarrow {BC} \Leftrightarrow \left\{ \begin{array}{l} - 3 - {x_I} = 0 - 0\\0 - {y_I} = - 3 - 0\\0 - {z_I} = 0 - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_I} = - 3\\{y_I} = 3\\{z_I} = 3\end{array} \right. \Rightarrow I\left( { - 3;3;3} \right)\)
+) Khi đó, \(M{A^2} + M{B^2} - M{C^2} = {\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2} - {\overrightarrow {MC} ^2} = {\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)^2} - {\left( {\overrightarrow {MI} + \overrightarrow {IC} } \right)^2}\)
\( = M{I^2} + 2\overrightarrow {MI} .\left( {\overrightarrow {IA} + \overrightarrow {IB} - \overrightarrow {IC} } \right) + I{A^2} + I{B^2} - I{C^2} = M{I^2} + I{A^2} + I{B^2} - I{C^2}\)
\(M{A^2} + M{B^2} - M{C^2}\) nhỏ nhất khi và chỉ khi \(MI\) ngắn nhất\( \Leftrightarrow M\) là hình chiếu vuông góc của I lên \(\left( {Oxy} \right)\).
\( \Leftrightarrow M\left( { - 3;3;0} \right)\)\( \Rightarrow {a^2} + {b^2} - {c^2} = {\left( { - 3} \right)^2} + {3^2} - 0 = 18\).
Chọn: A
Hàm số \(y = \dfrac{{{x^3}}}{3} - 3{x^2} + 5x + 2019\) nghịch biến trên khoảng nào trong các khoảng dưới đây?
\(y = \dfrac{{{x^3}}}{3} - 3{x^2} + 5x + 2019 \Rightarrow y' = {x^2} - 6x + 5\); \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 5\end{array} \right.\)
Hàm số \(y = \dfrac{{{x^3}}}{3} - 3{x^2} + 5x + 2019\) nghịch biến \(\left( {1;5} \right)\)
Chọn: D
Hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + 2\) đạt cực tiểu tại điểm \(x = 1\) và \(f\left( 1 \right) = - 3\). Tính \(b + 2a\).
Hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + 2\) đạt cực tiểu tại điểm \(x = 1\) và \(f\left( 1 \right) = - 3\)
\( \Leftrightarrow \left\{ \begin{array}{l}3 + 2a + b = 0\\6 + 2a > 0\\1 + a + b + 2 = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2a + b = - 3\\a + b = - 6\\a > - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = - 9\\a > - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = - 9\end{array} \right.\) \( \Rightarrow b + 2a = - 9 + 2.3 = - 3\).
Chọn: D
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng a. Diện tích S của mặt cầu ngoại tiếp hình lập phương đó là:
Hình lập phương \(ABCD.A'B'C'D'\) ,cạnh bằng a có bán kính mặt cầu ngoại tiếp \(R = \dfrac{{AC'}}{2} = \dfrac{{a\sqrt 3 }}{2}\)
Diện tích mặt cầu đó là: \(S = 4.\pi .{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)^2} = 3\pi {a^2}\).
Chọn: C
Trong không gian với hệ tọa độ \(Oxyz\), biết rằng tập hợp tất cả các điểm \(M\left( {x;y;z} \right)\) sao cho \(\left| x \right| + \left| y \right| + \left| z \right| = 3\) là một hình đa diện. Tính thể tích V của khối đa diện đó.
Tập hợp tất cả các điểm \(M\left( {x;y;z} \right)\) sao cho \(\left| x \right| + \left| y \right| + \left| z \right| = 3\) là hình bát diện đều SABCDS’ (như hình vẽ)
Thể tích V của khối đa diện đó :
\(V = 2.{V_{S.ABCD}} = 2.\dfrac{1}{3}.SO.{S_{ABCD}}\)
\(ABCD\) là hình vuông có cạnh \(BC = OB.\sqrt 2 = 3\sqrt 2 \)
\( \Rightarrow {S_{ABCD}} = {\left( {3\sqrt 2 } \right)^2} = 18\)
\( \Rightarrow V = 2.\dfrac{1}{3}.3.18 = 36\).
Chọn: B
Cho hàm số \(f\left( x \right)\) thỏa mãn \(f'\left( x \right) = 27 + \cos x\) và \(f\left( 0 \right) = 2019\). Mệnh đề nào dưới đây đúng?
\(f'\left( x \right) = 27 + \cos x \Rightarrow \int {f'\left( x \right)} dx = \int {\left( {27 + \cos x} \right)} dx \Rightarrow f\left( x \right) = 27x + \sin \,x + C\)
Mà \(f\left( 0 \right) = 2019\)\( \Rightarrow 27.0 + \sin 0 + C = 2019 \Leftrightarrow C = 2019\)\( \Rightarrow f\left( x \right) = 27x + \sin \,x + 2019\).
Chọn: C
Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng \(4\pi \). Thể tích khối trụ là
\(ABB'A'\) là hình vuông \( \Rightarrow h = 2r\)
Diện tích xung quanh của hình trụ : \({S_{xq}} = 2\pi rh = 2\pi r.2r = 4\pi {r^2} = 4\pi \,\, \Rightarrow r = 1 \Rightarrow h = 2\)
Thể tích khối trụ: \(V = \pi {r^2}h = \pi {.1^2}.2 = 2\pi \).
Chọn: B
Có bao nhiêu tiếp tuyến của đồ thị hàm số \(y = - {x^3} + 2{x^2}\) song song với đường thẳng \(y = x\)?
Gọi \(d\) là tiếp tuyến cần tìm, \(M\left( {{x_0};{y_0}} \right)\) là tiếp điểm. Ta có: \(y = - {x^3} + 2{x^2} \Rightarrow y' = - 3{x^2} + 4x\)
Do d song song với đường thẳng \(y = x\)\( \Rightarrow y'\left( {{x_0}} \right) = 1 \Leftrightarrow - 3x_0^2 + 4{x_0} = 1 \Leftrightarrow 3x_0^2 - 4{x_0} + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 1\\{x_0} = \dfrac{1}{3}\end{array} \right.\)
+) \({x_0} = 1 \Rightarrow {y_0} = 1 \Rightarrow \)Phương trình đường thẳng d là: \(y = 1.\left( {x - 1} \right) + 1 \Leftrightarrow y = x\): Loại
+) \({x_0} = \dfrac{1}{3} \Rightarrow {y_0} = \dfrac{5}{{27}} \Rightarrow \)Phương trình đường thẳng d là: \(y = 1.\left( {x - \dfrac{1}{3}} \right) + \dfrac{5}{{27}} \Leftrightarrow y = x - \dfrac{4}{{27}}\): Thỏa mãn
Vậy, có 1 tiếp tuyến của đồ thị hàm số \(y = - {x^3} + 2{x^2}\) song song với đường thẳng \(y = x\).
Chọn: D
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của m để phương trình \(f\left( {2 - \sqrt {2x - {x^2}} } \right) = m\) có nghiệm?
Xét hàm số \(t\left( x \right) = 2 - \sqrt {2x - {x^2}} ,\,\,x \in \left[ {0;2} \right]\), có \(t'\left( x \right) = \dfrac{{x - 1}}{{\sqrt {2x - {x^2}} }};\,\,t'\left( x \right) = 0 \Leftrightarrow x = 1\)
Hàm số \(t\left( x \right)\) liên tục trên \(\left[ {0;2} \right]\) có \(t\left( 0 \right) = t\left( 2 \right) = 2,\,\,t\left( 1 \right) = 1 \Rightarrow \mathop {\min }\limits_{\left[ {0;2} \right]} t\left( x \right) = 1,\,\,\mathop {\max }\limits_{\left[ {0;2} \right]} t\left( x \right) = 2\)
\(x \in \left[ {0;2} \right] \Rightarrow t \in \left[ {1;2} \right]\). Khi đó bài toán trở thành có bao nhiêu giá trị nguyên của m để phương trình \(f\left( t \right) = m\) có nghiệm \(t \in \left[ {1;2} \right]\).
Quan sát đồ thị hàm số \(y = f\left( t \right)\) trên đoạn \(\left[ {1;2} \right]\) ta thấy, phương trình \(f\left( t \right) = m\) có nghiệm \( \Leftrightarrow 3 \le m \le 5\)
Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {3;4;5} \right\}\): có 3 giá trị của m thỏa mãn.
Chọn: C
Tìm tọa độ điểm M trên trục Ox cách đều hai điểm \(A\left( {1;2; - 1} \right)\) và điểm \(B\left( {2;1;2} \right)\).
\(M \in Ox \Rightarrow M\left( {m;0;0} \right)\)
Theo đề bài, ta có:
\(\begin{array}{l}MA = MB \Leftrightarrow M{A^2} = M{B^2}\\ \Leftrightarrow {\left( {m - 1} \right)^2} + {2^2} + {1^2} = {\left( {m - 2} \right)^2} + {1^2} + {2^2} \Leftrightarrow {\left( {m - 1} \right)^2} = {\left( {m - 2} \right)^2}\\ \Leftrightarrow \left[ \begin{array}{l}m - 1 = m - 2\,\,\left( {Vo\,\,nghiem} \right)\\m - 1 = 2 - m\end{array} \right. \Leftrightarrow m = \dfrac{3}{2} \Rightarrow M\left( {\dfrac{3}{2};0;0} \right)\end{array}\)
Chọn: B
Tích \(\dfrac{1}{{2019!}}{\left( {1 - \dfrac{1}{2}} \right)^1}.{\left( {1 - \dfrac{1}{3}} \right)^2}.{\left( {1 - \dfrac{1}{4}} \right)^3}...{\left( {1 - \dfrac{1}{{2019}}} \right)^{2018}}\) được viết dưới dạng \({a^b}\), khi đó \(\left( {a;b} \right)\) là cặp nào trong các cặp sau?
\(\begin{array}{l}\,\,\,\,\dfrac{1}{{2019!}}{\left( {1 - \dfrac{1}{2}} \right)^1}.{\left( {1 - \dfrac{1}{3}} \right)^2}.{\left( {1 - \dfrac{1}{4}} \right)^3}...{\left( {1 - \dfrac{1}{{2019}}} \right)^{2018}}\\ = \dfrac{1}{{2019!}}.{\left( {\dfrac{1}{2}} \right)^1}.{\left( {\dfrac{2}{3}} \right)^2}.{\left( {\dfrac{3}{4}} \right)^3}...{\left( {\dfrac{{2018}}{{2019}}} \right)^{2018}}\\ = \dfrac{1}{{2019!}}.\dfrac{{1.2.3...2018}}{{{{2019}^{2018}}}} = \dfrac{1}{{{{2019}^{2019}}}} = {2019^{ - 2019}}\end{array}\)
Khi đó \(\left( {a;b} \right)\) là cặp \(\left( {2019; - 2019} \right)\).
Chọn: B
Gọi \(S = C_n^0 + C_n^1 + C_n^2 + ... + C_n^n\). Giá trị của S là bao nhiêu?
\(S = C_n^0 + C_n^1 + C_n^2 + ... + C_n^n = {\left( {1 + 1} \right)^n} = {2^n}\).
Chọn: D
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ: Đồ thị hàm số \(y = f\left( x \right)\) có mấy điểm cực trị?
Đồ thị hàm số \(y = f\left( x \right)\) có 2 điểm cực trị.
Chọn: B
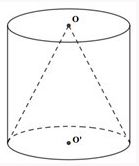
Một hình trụ có chiều cao h và bán kính đáy R. Hình nón có đỉnh là tâm đáy trên của hình trụ và đáy là hình tròn đáy dưới của hình trụ. Gọi \({V_1}\) là thể tích của hình trụ, \({V_2}\) là thể tích của hình nón. Tính tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\).
Nhận xét: Hai khối nón và khối trụ có cùng chiều cao \(h\) và cùng bán kính đáy bằng \(r\).
Ta có: \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\pi {r^2}h}}{{\dfrac{1}{3}\pi {r^2}h}} = 3\)
Chọn: C
Cho cấp số nhân \({u_1},\,{u_2},\,{u_3},...,{u_n}\) với công bội \(q\) \(\left( {q \ne 0,q \ne 1} \right)\). Đặt \({S_n} = {u_1} + {u_2} + ... + {u_n}\). Khi đó, ta có:
\({S_n} = \dfrac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}} \Leftrightarrow {S_n} = \dfrac{{{u_1}\left( {{q^n} - 1} \right)}}{{q - 1}}\).
Chọn: A
Khối hộp có 6 mặt đều là các hình thoi cạnh a, các góc nhọn của các mặt đều bằng \({60^0}\) có thể tích là
Giả sử các góc ở đỉnh A’ đều bằng \({60^0}\), khi đó tứ diện AA’B’D’ là tứ diện đều, có cạnh bằng a.
Gọi I là trung điểm của A’D’, G là trọng tâm tam giác đều A’B’D’.
\( \Rightarrow B'I = \dfrac{{a\sqrt 3 }}{2},\,\,\,B'G = \dfrac{2}{3}B'I = \dfrac{{a\sqrt 3 }}{3},\,\,\,\,{S_{A'B'D'}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
\(AG = \sqrt {AB{'^2} - B'{G^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{3}} = \sqrt {\dfrac{2}{3}} a\)
\({V_{A.A'B'D'}} = \dfrac{1}{3}AG.{S_{A'B'D'}} = \dfrac{1}{3}.\sqrt {\dfrac{2}{3}} .a.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 2 }}{{12}}\)
\({V_{ABCD.A'B'C'D'}} = 2{V_{ABD.A'B'D'}} = 6{V_{A.A'B'D'}} = 6.\dfrac{{{a^3}\sqrt 2 }}{{12}} = \dfrac{{{a^3}\sqrt 2 }}{2}\).
Chọn: D
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau và một điểm M không thuộc \(\left( P \right)\) và \(\left( Q \right)\). Qua M có bao nhiêu mặt phẳng vuông góc với \(\left( P \right)\) và \(\left( Q \right)\)?
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau và một điểm M không thuộc \(\left( P \right)\) và \(\left( Q \right)\). Qua M có vô số mặt phẳng vuông góc với \(\left( P \right)\) và \(\left( Q \right)\). Đó là các mặt phẳng chứa d, với d là đường thẳng qua M và vuông góc với \(\left( P \right)\) và \(\left( Q \right)\).
Chọn: D
Tính thể tích V của khối nón có bán kính đáy \(r = \sqrt 3 \) và chiều cao \(h = 4\).
Thể tích V của khối nón có bán kính đáy \(r = \sqrt 3 \) và chiều cao \(h = 4\) là: \(V = \dfrac{1}{3}\pi .{\left( {\sqrt 3 } \right)^2}.4 = 4\pi \).
Chọn: A
Cho hình bình hành ABCD với \(A\left( { - 2;3;1} \right),B\left( {3;0; - 1} \right),\,C\left( {6;5;0} \right)\). Tọa độ đỉnh D là
\(ABCD\) là hình bình hành\( \Rightarrow \overrightarrow {DC} = \overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}6 - {x_D} = 3 + 2\\5 - {y_D} = 0 - 3\\ - {z_D} = - 1 - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 1\\{y_D} = 8\\{z_D} = 2\end{array} \right.\,\, \Rightarrow \)\(D\left( {1;8;2} \right)\).
Chọn: C
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có đồ thị là đường cong trong hình vẽ bên dưới. Đặt \(g\left( x \right) = f\left( {{x^2}} \right)\). Tìm số nghiệm của phương trình \(g'\left( x \right) = 0\).
\(g\left( x \right) = f\left( {{x^2}} \right)\)\( \Rightarrow g'\left( x \right) = 2x.f'\left( x^2 \right)\)
\(g'\left( x \right) = 0 \Leftrightarrow 2x.f'\left( {{x^2}} \right) = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
f'\left( {{x^2}} \right) = 0 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
\left[ \matrix{
{x^2} = 0 \hfill \cr
{x^2} = c \hfill \cr} \right. \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = \pm \sqrt c \hfill \cr} \right.\)
(với \(2 < c < 3\), được biểu diễn trên hình vẽ bên)
Vậy, phương trình \(g'\left( x \right) = 0\) có 3 nghiệm.
Chọn: C
Cho hàm số \(f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) thỏa mãn \(f'\left( x \right) - 2018f\left( x \right) = 2018{x^{2017}}{e^{2018x}}\) với mọi \(x \in \mathbb{R}\), \(f\left( 0 \right) = 2018\). Tính \(f\left( 1 \right)\)?
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,f'\left( x \right) - 2018f\left( x \right) = 2018{x^{2017}}{e^{2018x}}\\ \Leftrightarrow {e^{ - 2018x}}f'\left( x \right) - 2018{e^{ - 2018x}}.f\left( x \right) = 2018{x^{2017}}\end{array}\)
\( \Rightarrow {\left( {{e^{ - 2018x}}f\left( x \right)} \right)^\prime } = 2018{x^{2017}} \Rightarrow {e^{ - 2018x}}f\left( x \right)\) là một nguyên hàm của \(2018{x^{2017}}\)
Ta có:
\(\int {2018{x^{2017}}} dx = {x^{2018}} + C\)\( \Rightarrow {e^{ - 2018x}}f\left( x \right) = {x^{2018}} + {C_0}\)
Mà \(f\left( 0 \right) = 2018\)\( \Rightarrow 2018 = {C_0}\, \Rightarrow {e^{ - 2018x}}f\left( x \right) = {x^{2018}} + 2018 \Leftrightarrow f\left( x \right) = {x^{2018}}{e^{2018x}} + 2018{e^{2018x}}\)
\( \Rightarrow f\left( 1 \right)\)\( = {e^{2018}} + 2018{e^{2018}} = 2019{e^{2018}}\).
Chọn: A
Tính thể tích của khối lập phương ABCD.A’B’C’D’ cạnh a.
Thể tích của khối lập phương ABCD.A’B’C’D’ cạnh a là : \({a^3}\)
Chọn: C
Trong không gian với hệ trục tọa độ Oxyz, cho \(\overrightarrow a = - \overrightarrow i + 2\overrightarrow j - 3\overrightarrow k \). Tọa độ của vectơ \(\overrightarrow a \) là
\(\overrightarrow a = - \overrightarrow i + 2\overrightarrow j - 3\overrightarrow k \Rightarrow \) Tọa độ của vectơ \(\overrightarrow a \) là : \(\left( { - 1;2; - 3} \right)\).
Chọn: C
Cho \({\log _3}x = 3{\log _3}2\). Khi đó giá trị của x là
Ta có: \({\log _3}x = 3{\log _3}2 \Leftrightarrow {\log _3}x = {\log _3}{2^3} \Leftrightarrow x = 8\).
Chọn: A
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh a, biết \(SA = SB\), \(SC = SD\), \(\left( {SAB} \right) \bot \left( {SCD} \right)\). Tổng diện tích hai tam giác SAB, SCD bằng \(\dfrac{{7{a^2}}}{{10}}\). Thể tích khối chóp \(S.ABCD\) là
Gọi I, J lần lượt là trung điểm của AB, CD.
\(\Delta SAB\) và \(\Delta SCD\) cân tại S\( \Rightarrow SI \bot AB,\,\,\,SJ \bot CD\)
Ta có: \(\left\{ \begin{array}{l}CD \bot SJ\\CD \bot IJ\end{array} \right. \Rightarrow CD \bot \left( {SIJ} \right) \Rightarrow \left( {SCD} \right) \bot \left( {SIJ} \right)\)
Tương tự : \(\left( {SAB} \right) \bot \left( {SIJ} \right)\) \( \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {SI;SJ} \right)} = \widehat {ISJ} = {90^0}\)
Kẻ \(SH \bot IJ\). Mà \(SH \subset \left( {SIJ} \right) \Rightarrow SH \bot CD \Rightarrow SH \bot \left( {ABCD} \right)\)
Ta có: \({S_{\Delta SAB}} + {S_{\Delta SCD}} = \dfrac{1}{2}.SI.AB + \dfrac{1}{2}.SJ.CD\)\( = \dfrac{1}{2}.SI.a + \dfrac{1}{2}.SJ.a = \dfrac{1}{2}.\left( {SI + SJ} \right).a = \dfrac{{7{a^2}}}{{10}}\)
\( \Rightarrow SI + SJ = \dfrac{{7a}}{5}\) (1)
\(\Delta SIJ\) vuông tại S \( \Rightarrow S{I^2} + S{J^2} = I{J^2} \Rightarrow {\left( {SI + SJ} \right)^2} - 2.SI.SJ = {a^2} \Leftrightarrow {\left( {\dfrac{{7a}}{5}} \right)^2} - 2.SI.SJ = {a^2}\)
\( \Leftrightarrow SI.SJ = \dfrac{{12{a^2}}}{{25}}\)
Ta có: \(SI.SJ = SH.IJ \Leftrightarrow \dfrac{{12{a^2}}}{{25}} = SH.a \Leftrightarrow SH = \dfrac{{12a}}{{25}}\)
Thể tích khối chóp \(S.ABCD\) là \(V = \dfrac{1}{3}SH.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{12a}}{{25}}.{a^2} = \dfrac{{4{a^3}}}{{25}}\).
Chọn: B
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn \(\left[ { - 2019;2019} \right]\) để đồ thị hàm số \(y = \dfrac{{2x + 1}}{{\sqrt {4{x^2} - 2x + m} }}\) có hai đường tiệm cận đứng?
Đồ thị hàm số có hai tiệm cận đứng \( \Rightarrow 4{x^2} - 2x + m = 0\) (1) có hai nghiệm phân biệt
+) \(x = - \dfrac{1}{2}\) là nghiệm của (1) \( \Leftrightarrow 4.{\left( { - \dfrac{1}{2}} \right)^2} - 2.\left( { - \dfrac{1}{2}} \right) + m = 0 \Leftrightarrow m = - 2\)
Khi đó, \(y = \dfrac{{2x + 1}}{{\sqrt {4{x^2} - 2x - 2} }}\) (TXĐ: \(D = \left( { - \dfrac{1}{2};1} \right)\))
\(\mathop {\lim }\limits_{x \to {{\left( { - \frac{1}{2}} \right)}^ + }} \dfrac{{2x + 1}}{{\sqrt {4{x^2} - 2x - 2} }} = \mathop {\lim }\limits_{x \to {{\left( { - \frac{1}{2}} \right)}^ + }} \dfrac{{2x + 1}}{{\sqrt {\left( {x - 1} \right)\left( {2x + 1} \right)} }} = \mathop {\lim }\limits_{x \to {{\left( { - \frac{1}{2}} \right)}^ + }} \sqrt {\dfrac{{2x + 1}}{{x - 1}}} = 0\)
\( \Rightarrow x = - \dfrac{1}{2}\) không phải TCĐ của đồ thị hàm số đã cho \( \Rightarrow \) Đồ thị hàm số có ít hơn 2 đường tiệm cận đứng \( \Rightarrow m = - 2\): Loại
+) \(x = - \dfrac{1}{2}\) là nghiệm của (1) \( \Leftrightarrow m \ne - 2\)
Khi đó, để có hai tiệm cận đứng thì (1) có 2 nghiệm phân biệt\( \Leftrightarrow \Delta ' > 0 \Leftrightarrow 1 - 4m > 0 \Leftrightarrow m < \dfrac{1}{4} \Rightarrow \left\{ \begin{array}{l}m < \dfrac{1}{4}\\m \ne - 2\end{array} \right.\)
Mà \(m \in \mathbb{Z},\,\,m \in \left[ { - 2019;2019} \right] \Rightarrow m \in \left\{ { - 2019; - 2018;...;0} \right\}\backslash \left\{ { - 2} \right\}\): Có 2019 số m thỏa mãn.
Chọn: D
Cho hai hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên \(\mathbb{R}\). Trong các mệnh đề sau, mệnh đề nào sai?
Mệnh đề sai là: \(\int {\left| {\dfrac{{f\left( x \right)}}{{g\left( x \right)}}} \right|dx} = \dfrac{{\int {f\left( x \right)dx} }}{{\int {g\left( x \right)dx} }}\), \(\left( {g\left( x \right) \ne 0,\,\,\forall x \in \mathbb{R}} \right)\).
Chọn: A
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 4x + 2y + 6z - 1 = 0\). Tâm của mặt cầu là
\(\left( S \right):{x^2} + {y^2} + {z^2} - 4x + 2y + 6z - 1 = 0\) có tâm \(I\left( {2; - 1; - 3} \right)\).
Chọn: C
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có \(f\left( 1 \right) = 1,\,\,f\left( { - 1} \right) = - \dfrac{1}{3}\). Đặt \(g\left( x \right) = {f^2}\left( x \right) - 4f\left( x \right)\). Cho biết đồ thị của \(y = f'\left( x \right)\) có dạng như hình vẽ dưới đây.
Mệnh đề nào sau đây đúng?
Bảng biến thiên của \(y = f\left( x \right)\):
\( \Rightarrow f\left( x \right) \le 1,\forall x\)
Ta có: \(g\left( x \right) = {f^2}\left( x \right) - 4f\left( x \right) \Rightarrow g'\left( x \right) = 2f\left( x \right).f'\left( x \right) - 4f'\left( x \right) = 2f'\left( x \right).\left( {f\left( x \right) - 2} \right)\)
Mà \(f\left( x \right) - 2 < 0,\,\,\forall x\) (do \(f\left( x \right) \le 1,\forall x\))
Ta có bảng biến thiên của \(y = g\left( x \right)\) như sau:
Chọn: B
Đầu năm 2016, Curtis Cooper và các cộng sự tại nhóm nghiên cứu Đại học Central Mis-souri, Mỹ công bố số nguyên tố lớn nhất tại thời điểm đó. Số nguyên tố này là một dạng Mersenne, có giá trị bằng \(M = {2^{74207281}} - 1\). Hỏi M có bao nhiêu chữ số?
+) Xác định số chữ số của \(M + 1 = {2^{74207281}}\)
Tìm số tự nhiên n thỏa mãn \({10^n} \le {2^{74207281}} < {10^{n + 1}} \Leftrightarrow \left\{ \begin{array}{l}{10^n} \le {2^{74207281}}\\{10^{n + 1}} > {2^{74207281}}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}n \le \log \left( {{2^{74207281}}} \right)\\n + 1 > \log \left( {{2^{74207281}}} \right)\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}n \le 74207281.\log 2 \approx 22338617,5\\n > 74207281.\log 2 - 1 \approx 22338616,5\end{array} \right. \Leftrightarrow n = 22338617\)
Vậy, \(M + 1 = {2^{74207281}}\) có \(n + 1 = \)22338618 chữ số
+) Xác định số chữ số của \(M = {2^{74207281}} - 1\)
Nhận xét: Do \(M + 1\) là số có 22338618 chữ số nên \(M\) hoặc có 22338618 chữ số hoặc có 22338617 chữ số.
\(M\) có 22338617 khi và chỉ khi \(M + 1 = {10^{22338617}}\), tức là: \({2^{74\,207\,281}} = {10^{22\,338\,617}} \Leftrightarrow {2^{51\,868664}} = {5^{22\,338\,617}}\): vô lí, do 2 là số chẵn, 5 là số lẻ.
Vậy, \(M = {2^{74207281}} - 1\) là số có \(22338618\) chữ số.
Chọn: D
Có bao nhiêu giá trị thực của m để bất phương trình \(\left( {2m + 2} \right)\left( {x + 1} \right)\left( {{x^3} - 1} \right) - \left( {{m^2} + m + 1} \right)\left( {{x^2} - 1} \right) + 2x + 2 < 0\) vô nghiệm?
Ta có: \(\left( {2m + 2} \right)\left( {x + 1} \right)\left( {{x^3} - 1} \right) - \left( {{m^2} + m + 1} \right)\left( {{x^2} - 1} \right) + 2x + 2 < 0\)
\(\begin{array}{l} \Leftrightarrow \left( {x + 1} \right)\left[ {\left( {2m + 2} \right)\left( {{x^3} - 1} \right) - \left( {{m^2} + m + 1} \right)\left( {x - 1} \right) + 2} \right] < 0\\ \Leftrightarrow \left( {x + 1} \right)\left[ {\left( {2m + 2} \right){x^3} - \left( {2m + 2} \right) - \left( {{m^2} + m + 1} \right)x + \left( {{m^2} + m + 1} \right) + 2} \right] < 0\\ \Leftrightarrow \left( {x + 1} \right)\left[ {\left( {2m + 2} \right){x^3} - \left( {{m^2} + m + 1} \right)x + \left( {{m^2} - m + 1} \right)} \right] < 0\,\,\,(*)\end{array}\)
(*) vô nghiệm \( \Leftrightarrow \)\(\left( {x + 1} \right)\left[ {\left( {2m + 2} \right){x^3} - \left( {{m^2} + m + 1} \right)x + \left( {{m^2} - m + 1} \right)} \right] \ge 0\) (2*) luôn đúng với mọi x
\( \Rightarrow x = - 1\) là nghiệm của \(\left( {2m + 2} \right){x^3} - \left( {{m^2} + m + 1} \right)x + \left( {{m^2} - m + 1} \right) = 0\)
\( \Rightarrow - \left( {2m + 2} \right) + \left( {{m^2} + m + 1} \right) + \left( {{m^2} - m + 1} \right) = 0 \Leftrightarrow 2{m^2} - 2m = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 1\end{array} \right.\)
+) \(m = 0\):
\((2*) \Leftrightarrow \left( {x + 1} \right)\left( {2{x^3} - x + 1} \right) \ge 0 \Leftrightarrow {\left( {x + 1} \right)^2}\left( {2{x^2} - 2x + 1} \right) \ge 0\) luôn đúng với mọi x
\( \Rightarrow m = 0\) : Thỏa mãn.
+) \(m = 1\):
\((2*) \Leftrightarrow \left( {x + 1} \right)\left( {4{x^3} - 3x + 1} \right) \ge 0 \Leftrightarrow {\left( {x + 1} \right)^2}\left( {4{x^2} - 4x + 1} \right) \ge 0 \Leftrightarrow {\left( {x + 1} \right)^2}{\left( {2x - 1} \right)^2} \ge 0\) luôn đúng với mọi x
\( \Rightarrow m = 1\) : Thỏa mãn.
Vậy có 2 giá trị của m thỏa mãn.
Chọn: D
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Hai điểm \(M,N\) thuộc các cạnh \(AB\) và \(AD\) (M, N không trùng với A, B, D). Sao cho \(\dfrac{{AB}}{{AM}} + 2.\dfrac{{AD}}{{AN}} = 4\). Kí hiệu \(V,\,{V_1}\) lần lượt là thể tích của các khối chóp \(S.ABCD\) và \(S.MBCDN\). Tìm giá trị lớn nhất của tỉ số \(\dfrac{{{V_1}}}{V}\).
Do các khối chóp \(S.ABCD\) và \(S.MBCDN\) có cùng chiều cao kẻ từ S nên \(\dfrac{{{V_1}}}{V} = \dfrac{{{S_{MBCDN}}}}{{{S_{ABCD}}}}\)
Ta có: \(\dfrac{{AB}}{{AM}} + 2.\dfrac{{AD}}{{AN}} = 4\). Áp dụng BĐT Cô si, ta có:
\(\dfrac{{AB}}{{AM}} + 2.\dfrac{{AD}}{{AN}} \ge 2\sqrt {\dfrac{{AB}}{{AM}}.2.\dfrac{{AD}}{{AN}}} = 2\sqrt 2 .\sqrt {\dfrac{{AB.AD}}{{AM.AN}}} \)(với \(\dfrac{{AB}}{{AM}} > 1,\,\,\dfrac{{AD}}{{AN}} > 1\))
\( \Rightarrow 2\sqrt 2 .\sqrt {\dfrac{{AB.AD}}{{AM.AN}}} \le 4 \Leftrightarrow \dfrac{{AB.AD}}{{AM.AN}} \le 2\)
\( \Rightarrow \dfrac{{{S_{\Delta ABD}}}}{{{S_{\Delta AMN}}}} \le 2 \Rightarrow \dfrac{{{S_{\Delta ABCD}}}}{{{S_{\Delta AMN}}}} \le 4\) (do \({S_{\Delta ABD}} = \dfrac{1}{2}{S_{\Delta ABCD}}\))\( \Rightarrow \dfrac{{{S_{\Delta AMN}}}}{{{S_{\Delta ABCD}}}} \ge \dfrac{1}{4}\)\( \Rightarrow \dfrac{{{S_{MBCDN}}}}{{{S_{ABCD}}}} \le \dfrac{3}{4} \Rightarrow \)\(\dfrac{{{V_1}}}{V} \le \dfrac{3}{4}\)
Tỉ số \(\dfrac{{{V_1}}}{V}\) đạt giá trị lớn nhất bằng \(\dfrac{3}{4}\) khi và chỉ khi \(\left\{ \begin{array}{l}\dfrac{{AB}}{{AM}} + 2.\dfrac{{AD}}{{AN}} = 4\\\dfrac{{AB}}{{AM}} = 2.\dfrac{{AD}}{{AN}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{AB}}{{AM}} = 2\\\dfrac{{AD}}{{AN}} = 1\end{array} \right.\)
Chọn: B
Cho hàm số \(y = \left| {{{\sin }^3}x - m.\sin \,x + 1} \right|\). Gọi S là tập hợp tất cả các số tự nhiên m sao cho hàm số đồng biến trên \(\left( {0;\dfrac{\pi }{2}} \right)\). Tính số phần tử của S?
Trên khoảng \(\left( {0;\dfrac{\pi }{2}} \right)\), hàm số \(y = \sin \,x\)đồng biến.
Đặt \(t = \sin x,\,\,x \in \left( {0;\dfrac{\pi }{2}} \right) \Rightarrow t \in \left( {0;1} \right)\) .
Khi đó, hàm số\(y = \left| {{{\sin }^3}x - m.\sin \,x + 1} \right|\) đồng biến trên \(\left( {0;\dfrac{\pi }{2}} \right)\) khi và chỉ khi \(y = f\left( t \right) = \left| {{t^3} - mt + 1} \right|\) đồng biến trên \(\left( {0;1} \right)\).
Xét hàm số \(y = f\left( t \right) = {t^3} - mt + 1\) trên khoảng \(\left( {0;1} \right)\), có :\(f'\left( t \right) = 3{t^2} - m\)
+) Khi \(m = 0\): \(f'\left( x \right) = 3{x^2} \ge 0,\,\,\forall x\)\( \Rightarrow y = f\left( x \right) = {x^3} + 1\) đồng biến trên \(\left( {0;1} \right)\)
Và đồ thị hàm số \(y = f\left( x \right) = {x^3} + 1\) cắt Ox tại điểm duy nhất là \(x = - 1 \in \left( {0;1} \right)\)
\( \Rightarrow \)\(y = g\left( x \right) = \left| {{x^3} - m\,x + 1} \right|\) đồng biến trên \(\left( {0;1} \right)\) \( \Rightarrow m = 0\): thỏa mãn.
+) \(m > 0\): \(f'\left( x \right) = 0\) có 2 nghiệm phân biệt \({x_1} = - \sqrt {\dfrac{m}{3}} ,\,\,{x_2} = \sqrt {\dfrac{m}{3}} \)
Hàm số \(y = f\left( x \right) = {x^3} - m\,x + 1\) đồng biến trên các khoảng \(\left( { - \infty ; - \sqrt {\dfrac{m}{3}} } \right)\) và \(\left( {\sqrt {\dfrac{m}{3}} ; + \infty } \right)\)
Nhận xét: \(\left( {0;1} \right) \not\subset \left( {\sqrt {\dfrac{m}{3}} ; + \infty } \right)\) , \(\left( {0;1} \right) \not\subset \left( { - \infty ; - \sqrt {\dfrac{m}{3}} } \right)\) , \(\forall m > 0\)
TH1: \( - \sqrt {\dfrac{m}{3}} < 0 < \sqrt {\dfrac{m}{3}} < 1 \Leftrightarrow 0 < m < 3\)
Để \(y = g\left( x \right) = \left| {{x^3} - m\,x + 1} \right|\) đồng biến trên \(\left( {0;1} \right)\) thì \({x^3} - m\,x + 1 = 0\) có nghiệm (bội lẻ) là \(x = \sqrt {\dfrac{m}{3}} \)
\( \Rightarrow \dfrac{{m\sqrt m }}{{3\sqrt 3 }} - \dfrac{{m\sqrt m }}{{\sqrt 3 }} + 1 = 0 \Leftrightarrow - 2m\sqrt m + 3\sqrt 3 = 0 \Leftrightarrow m\sqrt m = \dfrac{{3\sqrt 3 }}{2} \Leftrightarrow m = \dfrac{3}{{\sqrt[3]{4}}}\) (thỏa mãn)
TH2: \( - \sqrt {\dfrac{m}{3}} < 0 < 1 \le \sqrt {\dfrac{m}{3}} \Leftrightarrow m \ge 3\)
Để \(y = g\left( x \right) = \left| {{x^3} - m\,x + 1} \right|\) đồng biến trên \(\left( {0;1} \right)\) thì \({x^3} - m\,x + 1 \le 0,\,\,\forall x \in \left( {0;1} \right)\)
\( \Leftrightarrow mx \le {x^3} + 1,\,\,\forall x \in \left( {0;1} \right) \Leftrightarrow m \le {x^2} + \dfrac{1}{x},\,\,\forall x \in \left( {0;1} \right)\)
Xét hàm số \(y = {x^2} + \dfrac{1}{x},\,\,x \in \left( {0;1} \right)\, \Rightarrow y' = 2x - \dfrac{1}{{{x^2}}}\); \(y' = 0 \Leftrightarrow x = \dfrac{1}{{\sqrt[3]{2}}} \in \left( {0;1} \right)\)
Hàm số liên tục trên \(\left( {0;1} \right)\) và \(y\left( {\dfrac{1}{{\sqrt[3]{2}}}} \right) = \dfrac{3}{{\sqrt[3]{4}}};\,\,\,y\left( 1 \right) = 2;\,\,\mathop {\lim }\limits_{x \to {0^ + }} y = \, + \infty \, \Rightarrow \mathop {\min }\limits_{\left( {0;1} \right)} y = \dfrac{3}{{\sqrt[3]{4}}}\)
Để \(m \le {x^2} + \dfrac{1}{x},\,\,\forall x \in \left( {0;1} \right)\) thì \(m \le \dfrac{3}{{\sqrt[3]{4}}} \Rightarrow \)Không có giá trị của m thỏa mãn.
Vậy, chỉ có giá trị \(m = 0\) thỏa mãn.
Chọn: A
Cho hình chóp \(S.\,ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và \(\widehat {ABC} = 60^\circ \). Hình chiếu vuông góc của điểm \(S\) lên mặt phẳng \(\left( {ABCD} \right)\) trùng với trọng tâm tam giác \(ABC\). Gọi \(\varphi \) là góc giữa đường thẳng \(SB\) với mặt phẳng \(\left( {SCD} \right)\), tính \(\sin \varphi \) biết rằng \(SB = a\).
Gọi \(M\) là trung điểm của \(SD\), nhận xét góc giữa \(SB\) và \(\left( {SCD} \right)\) cũng bằng góc giữa \(OM\) và \(\left( {SCD} \right)\) (Vì \(OM//SB\))
Gọi \(H\) là hình chiếu của \(O\) trên \(\left( {SCD} \right)\) \( \Rightarrow \widehat {\left( {OM,\left( {SCD} \right)} \right)} = \widehat {\left( {OM,MH} \right)} = \widehat {OMH}\).
Trong \(\left( {SBD} \right)\) kẻ \(OE//SH\), khi đó tứ diện \(OECD\) là tứ diện vuông nên \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{C^2}}} + \dfrac{1}{{O{D^2}}} + \dfrac{1}{{O{E^2}}}\).
Ta dễ dàng tính được \(OC = \dfrac{a}{2},OD = \dfrac{{a\sqrt 3 }}{2}\).
Lại có: \(\dfrac{{OE}}{{SH}} = \dfrac{{OD}}{{HD}} = \dfrac{3}{4} \Rightarrow OE = \dfrac{3}{4}SH\), mà \(SH = \sqrt {S{B^2} - B{H^2}} = \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}} = \dfrac{{a\sqrt 6 }}{3}\)
Do đó \(OE = \dfrac{3}{4}SH = \dfrac{3}{4}.\dfrac{{a\sqrt 6 }}{3} = \dfrac{{a\sqrt 6 }}{4}\).
Suy ra \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{{{\left( {a/2} \right)}^2}}} + \dfrac{1}{{{{\left( {a\sqrt 3 /2} \right)}^2}}} + \dfrac{1}{{{{\left( {a\sqrt 6 /4} \right)}^2}}} = \dfrac{8}{{{a^2}}} \Rightarrow OH = \dfrac{{a\sqrt 2 }}{4}\).
Tam giác \(OMH\) vuông tại \(H\) có \(OM = \dfrac{1}{2}SB = \dfrac{a}{2},OH = \dfrac{{a\sqrt 2 }}{4} \Rightarrow \sin \widehat {OMH} = \dfrac{{OH}}{{OM}} = \dfrac{{\sqrt 2 }}{2}\).
Vậy \(\sin \varphi = \dfrac{{\sqrt 2 }}{2}\).
Chọn D.
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {x^2}\left( {x - 2} \right)\left( {{x^2} - 6x + m} \right)\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu số nguyên \(m\) thuộc đoạn \(\left[ { - 2019;\,2019} \right]\) để hàm số \(g\left( x \right) = f\left( {1 - x} \right)\) nghịch biến trên khoảng \(\left( { - \infty ;\, - 1} \right)\)?
Ta có: \(g'\left( x \right) = - f'\left( {1 - x} \right) = - {\left( {1 - x} \right)^2}\left( {1 - x - 2} \right)\left[ {{{\left( {1 - x} \right)}^2} - 6\left( {1 - x} \right) + m} \right]\) \( = - {\left( {1 - x} \right)^2}\left( { - 1 - x} \right)\left( {{x^2} + 4x + m - 5} \right) = {\left( {x - 1} \right)^2}\left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right)\)
Hàm số \(g\left( x \right)\) nghịch biến trên \(\left( { - \infty ; - 1} \right)\)
\( \Leftrightarrow g'\left( x \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right) \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right)\)
\( \Leftrightarrow {x^2} + 4x + m - 5 \ge 0,\forall x \in \left( { - \infty ; - 1} \right)\) (do \(x + 1 < 0,\forall x \in \left( { - \infty ; - 1} \right)\))
\( \Leftrightarrow h\left( x \right) = {x^2} + 4x - 5 \ge - m\,\,\forall x \in \left( { - \infty - 1} \right) \Leftrightarrow - m \le \mathop {\min }\limits_{\left( { - \infty - 1} \right]} h\left( x \right)\).
Ta có \(h'\left( x \right) = 2x + 4 = 0 \Leftrightarrow x = - 2\).
BBT:
Dựa vào BBT ta có \( - m \le - 9 \Leftrightarrow m \ge 9\).
Mà \(m \in \left[ { - 2019;2019} \right]\) và \(m\) nguyên nên \(m \in \left[ {9;10;11;...;2019} \right]\) hay có \(2019 - 9 + 1 = 2011\) giá trị của \(m\) thỏa mãn.
Chọn C.
Cho hình chóp \(S.\,ABC\) có \(AB = AC = 4,\,BC = 2,\,SA = 4\sqrt 3 \), . Tính thể tích khối chóp \(S.\,ABC.\)
Dễ thấy \(\Delta SAB = \Delta SAC\left( {c.g.c} \right)\) nên \(SB = SC\) hay tam giác \(\Delta SBC\) cân.
Gọi \(M\) là trung điểm \(BC\) ta có: \(AM \bot BC,SM \bot BC \Rightarrow BC \bot \left( {SAM} \right)\).
Gọi \(H\) là hình chiếu của \(S\) trên \(AM\) thì \(SH \bot AM,SH \bot BC\) nên \(SH\) là đường cao của hình chóp.
Xét tam giác \(SAB\) có: \(S{B^2} = S{A^2} + A{B^2} - 2SA.AB\cos {30^0} = 16 \Rightarrow SB = 4 \Rightarrow SC = 4\).
Do đó \(S{M^2} = \dfrac{{S{B^2} + S{C^2}}}{2} - \dfrac{{B{C^2}}}{4} = 15 \Rightarrow SM = \sqrt {15} \).
Tam giác \(ABC\) có \(A{M^2} = \dfrac{{A{B^2} + A{C^2}}}{2} - \dfrac{{B{C^2}}}{4} = 15 \Rightarrow AM = \sqrt {15} \).
Khi đó \({S_{SAM}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = 6\).
Do đó: \(SH = \dfrac{{2{S_{SAM}}}}{{AM}} = \dfrac{{2.6}}{{\sqrt {15} }} = \dfrac{{4\sqrt {15} }}{5}\).
\({V_{S.ABC}} = \dfrac{1}{3}{S_{ABC}}.SH = \dfrac{1}{3}.\dfrac{1}{2}AM.BC.SH = \dfrac{1}{6}.\sqrt {15} .2.\dfrac{{4\sqrt {15} }}{5} = 4\).
Chọn C.
Cho phương trình \(\left( {2\sin x - 1} \right)\left( {\sqrt 3 \tan x + 2\sin x} \right) = 3 - 4{\cos ^2}x\). Tổng tất cả các nghiệm thuộc đoạn \(\left[ {0;\,20\pi } \right]\) của phương trình bằng
\(\left( {2\sin x - 1} \right)\left( {\sqrt 3 \tan x + 2\sin x} \right) = 3 - 4{\cos ^2}x\,\,\left( * \right)\)
Điều kiện: \(\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \).
\(\begin{array}{l}\left( * \right) \Leftrightarrow \left( {2\sin x - 1} \right).\dfrac{{\sqrt 3 \sin x + 2\sin x\cos x}}{{\cos x}} = 3 - 4{\cos ^2}x\\ \Leftrightarrow \left( {2\sin x - 1} \right)\left( {\sqrt 3 \sin x + \sin 2x} \right) + \left( {4{{\cos }^3}x - 3\cos x} \right) = 0\\ \Leftrightarrow 2\sqrt 3 {\sin ^2}x - \sqrt 3 \sin x + 2\sin x\sin 2x - \sin 2x + \cos 3x = 0\\ \Leftrightarrow 2\sqrt 3 {\sin ^2}x - \sqrt 3 \sin x + \cos x - \cos 3x - \sin 2x + \cos 3x = 0\\ \Leftrightarrow \sqrt 3 \sin x\left( {2\sin x - 1} \right) - \sin 2x + \cos x = 0\\ \Leftrightarrow \sqrt 3 \sin x\left( {2\sin x - 1} \right) - \cos x\left( {2\sin x - 1} \right) = 0\\ \Leftrightarrow \left( {2\sin x - 1} \right)\left( {\sqrt 3 \sin x - \cos x} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2\sin x - 1 = 0\,\,\left( 1 \right)\\\sqrt 3 \sin x - \cos x = 0\,\,\left( 2 \right)\end{array} \right.\end{array}\)
Giải \(\left( 1 \right) \Leftrightarrow \sin x = \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\).
Giải \(\left( 2 \right) \Leftrightarrow \sqrt 3 \sin x = \cos x \Leftrightarrow \sqrt 3 \tan x = 1 \Leftrightarrow \tan x = \dfrac{1}{{\sqrt 3 }} \Leftrightarrow x = \dfrac{\pi }{6} + k\pi \left( {TM} \right)\).
Hợp nghiệm của \(\left( 1 \right)\) và \(\left( 2 \right)\) ta được \(\left[ \begin{array}{l}x = \dfrac{\pi }{6} + k\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
Mà \(x \in \left[ {0;20\pi } \right] \Rightarrow x \in \left\{ {\dfrac{\pi }{6};\dfrac{\pi }{6} + \pi ;...;\dfrac{\pi }{6} + 19\pi ;\dfrac{{5\pi }}{6};\dfrac{{5\pi }}{6} + 2\pi ;...\dfrac{{5\pi }}{6} + 18\pi } \right\}\)
Vậy tổng các nghiệm là:
\(\begin{array}{l}\,\,\,\,\,\dfrac{\pi }{6} + \dfrac{\pi }{6} + \pi + \dfrac{\pi }{6} + 2\pi + ... + \dfrac{\pi }{6} + 19\pi + \dfrac{{5\pi }}{6} + \dfrac{{5\pi }}{6} + 2\pi + ... + \dfrac{{5\pi }}{6} + 18\pi \\ = 20.\dfrac{\pi }{6} + \left( {1 + 2 + 3 + ... + 19} \right)\pi + \dfrac{{5\pi }}{6}.10 + 2\pi \left( {1 + 2 + ... + 9} \right) = \dfrac{{875\pi }}{3}\end{array}\).
Chọn D.
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(A\), \(AB = a\sqrt 3 \), \(BC = 2a\), đường thẳng \(AC'\) tạo với mặt phẳng \(\left( {BCC'B'} \right)\) một góc \(30^\circ \). Diện tích của mặt cầu ngoại tiếp hình lăng trụ đã cho bằng
Trong mặt phẳng \(\left( {ABC} \right)\) kẻ \(AH \bot BC\left( {H \in BC} \right)\).
Lại có \(AH \bot BB'\) (do \(BB \bot \left( {ABC} \right)\) suy ra \(AH \bot \left( {BCC'B'} \right)\).
Suy ra \(\widehat {\left( {AC',\left( {BCC'B'} \right)} \right)} = \widehat {AC'H} = {30^0}\).
Ta có: \(AC = \sqrt {B{C^2} - A{B^2}} = a,AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{a\sqrt 3 }}{2}\)
\(AC' = \dfrac{{AH}}{{\sin \widehat {AC'H}}} = a\sqrt 3 \) \( \Rightarrow CC' = \sqrt {AC{'^2} - A{C^2}} = a\sqrt 2 \).
Gọi \(R\) là bán kính mặt cầu ngoại tiếp lăng trụ, khi đó \(R = \sqrt {{r^2} + \dfrac{{{h^2}}}{4}} \) với \(r = \dfrac{{BC}}{2} = a\) là bán kính đường tròn ngoại tiếp tam giác vuông \(ABC\) và \(h = CC' = a\sqrt 2 \)
Do đó \(R = \sqrt {{a^2} + \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 6 }}{2} \Rightarrow S = 4\pi {R^2} = 4\pi .\dfrac{{6{a^2}}}{4} = 6\pi {a^2}\).
Chọn A.
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) thỏa mãn các điều kiện: \(f\left( 0 \right) = 2\sqrt 2 \), \(f\left( x \right) > 0,\forall x \in \mathbb{R}\) và \(f\left( x \right).f'\left( x \right) = \left( {2x + 1} \right)\sqrt {1 + {f^2}\left( x \right)} ,\,\forall x \in \mathbb{R}\). Khi đó giá trị \(f\left( 1 \right)\) bằng
Ta có: \(f\left( x \right).f'\left( x \right) = \left( {2x + 1} \right)\sqrt {1 + {f^2}\left( x \right)} \)
\( \Rightarrow \dfrac{{f\left( x \right).f'\left( x \right)}}{{\sqrt {1 + {f^2}\left( x \right)} }} = 2x + 1 \Rightarrow \int {\dfrac{{f\left( x \right).f'\left( x \right)}}{{\sqrt {1 + {f^2}\left( x \right)} }}dx} = \int {\left( {2x + 1} \right)dx} \)
Tính \(\int {\dfrac{{f\left( x \right).f'\left( x \right)}}{{\sqrt {1 + {f^2}\left( x \right)} }}dx} \) ta đặt \(\sqrt {1 + {f^2}\left( x \right)} = t \Rightarrow 1 + {f^2}\left( x \right) = {t^2} \Rightarrow 2f\left( x \right)f'\left( x \right)dx = 2tdt\) \( \Rightarrow f\left( x \right)f'\left( x \right)dx = tdt\)
Thay vào ta được \(\int {\dfrac{{f\left( x \right).f'\left( x \right)}}{{\sqrt {1 + {f^2}\left( x \right)} }}dx} = \int {\dfrac{{tdt}}{t}} = \int {dt} = t + C = \sqrt {1 + {f^2}\left( x \right)} + C\)
Do đó \(\sqrt {1 + {f^2}\left( x \right)} + C = {x^2} + x\).
\(f\left( 0 \right) = 2\sqrt 2 \Rightarrow \sqrt {1 + {{\left( {2\sqrt 2 } \right)}^2}} + C = 0 \Leftrightarrow C = - 3\).
Từ đó:
\(\begin{array}{l}\sqrt {1 + {f^2}\left( x \right)} - 3 = {x^2} + x \Rightarrow \sqrt {1 + {f^2}\left( 1 \right)} - 3 = 1 + 1 \Leftrightarrow \sqrt {1 + {f^2}\left( 1 \right)} = 5\\ \Leftrightarrow 1 + {f^2}\left( 1 \right) = 25 \Leftrightarrow {f^2}\left( 1 \right) = 24 \Leftrightarrow f\left( 1 \right) = \sqrt {24} \end{array}\)
Chọn C.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)



