Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón
I. Sơ đồ Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón

II. Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón
1. Các kiến thức cần nhớ
Hình nón
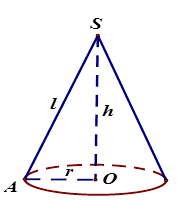
Cho hình nón có bán kính đáy $R = OA$, đường sinh $l = SA$, chiều cao $h = SO$. Khi đó :
+ Diện tích xung quanh: ${S_{xq}} = \pi Rl$
+ Diện tích đáy : \({S_d} = \pi {R^2}\)
+ Diện tích toàn phần: ${S_{tp}} = {S_{xq}} + {S_d} = \pi Rl + \pi {R^2}$
+ Thể tích: $V = \dfrac{1}{3}\pi {R^2}h$
+ Công thức liên hệ : ${R^2} + {h^2} = {l^2}$
Hình nón cụt
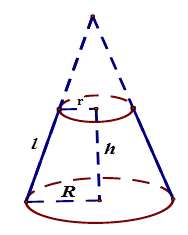
Cho hình nón cụt có các bán kính đáy là $R$ và $r,$chiều cao $h,$ đường sinh $l.$
+ Diện tích xung quanh: ${S_{xq}} = \pi (R + r)l$
+ Diện tích toàn phần: ${S_{tp}} = \pi (R + r)l + \pi {R^2} + \pi {r^2}$
+ Thể tích: $V = \dfrac{1}{3}\pi h({R^2} + Rr + {r^2})$
2. Các dạng toán thường gặp
Dạng 1: Tính diện tích, thể tích và các đại lượng liên quan của hình nón và hình nón cụt
Phương pháp:
Ta sử dụng các công thức ở phần lý thuyết
* Cho hình nón có bán kính đáy $R = OA$, đường sinh $l = SA$, chiều cao $h = SO$. Khi đó :
+ Diện tích xung quanh: ${S_{xq}} = \pi Rl.$
+ Diện tích toàn phần: ${S_{tp}} = \pi Rl + \pi {R^2}.$
+ Thể tích: $V = \dfrac{1}{3}\pi {R^2}h.$
+ Công thức liên hệ : ${R^2} + {h^2} = {l^2}$
* Cho hình nón cụt có các bán kính đáy là $R$ và $r,$chiều cao $h,$ đường sinh $l.$
+ Diện tích xung quanh: ${S_{xq}} = \pi (R + r)l.$
+ Diện tích toàn phần: ${S_{tp}} = \pi (R + r)l + \pi {R^2} + \pi {r^2}.$
+ Thể tích: $V = \dfrac{1}{3}\pi h({R^2} + Rr + {r^2}).$
