Khảo sát sự biến thiên và vẽ đồ thị của hàm số (hàm đa thức bậc ba)

Lý thuyết về khảo sát sự biến thiên và vẽ đồ thị của hàm đa thức bậc ba môn toán lớp 12 với nhiều dạng bài cùng phương pháp giải nhanh kèm bài tập vận dụng
(407) 1358 26/07/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    Hàm số bậc ba: \(y = a{x^3} + b{x^2} + cx + d\left( {a \ne 0} \right)\)

    +) TXĐ: $D = R$
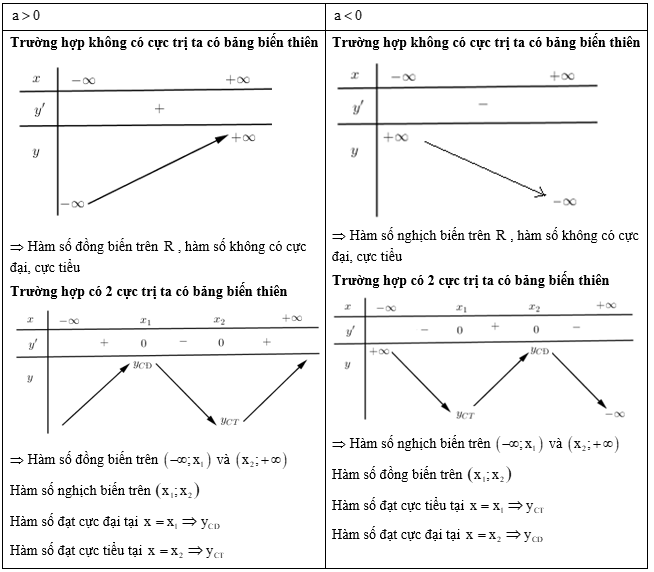
    +) Sự biến thiên:

    \(y' = 3a{x^2} + 2bx + c\)

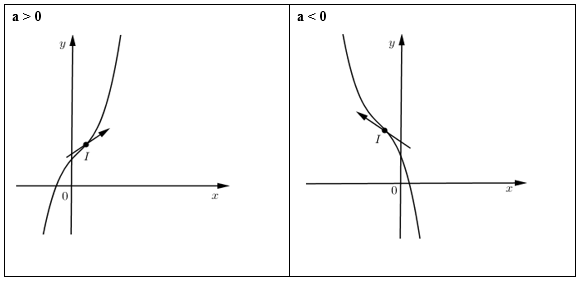
    \(y' = 0\) có hai nghiệm phân biệt \({x_1},{x_2} \Rightarrow \) có cực trị.

    \(y' = 0\) vô nghiệm hoặc có nghiệm kép \( \Rightarrow \) không có cực trị.

    +) Đồ thị:

    - Điểm uốn \(I\left( {{x_0};{y_0}} \right)\) với \({x_0}\) là nghiệm của phương trình \(y'' = 0\) và \({y_0} = f\left( {{x_0}} \right)\).

    TH1: \(y' = 0\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' = {b^2} - 3ac > 0\) 

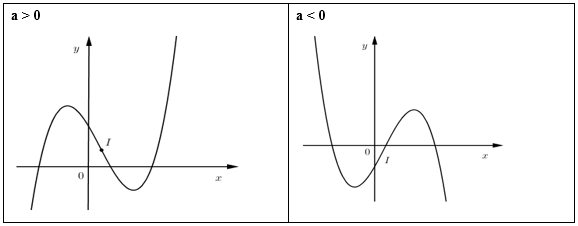
    TH2:\(y' = 0\) có nghiệm kép \( \Leftrightarrow \Delta ' = {b^2} - 3ac = 0\)

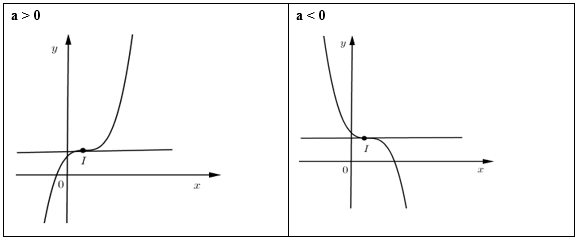
    TH3: \(y' = 0\) vô nghiệm \( \Leftrightarrow \Delta ' = {b^2} - 3ac < 0\)

    Xem toàn bộ nội dung Toán 12:

    (407) 1358 26/07/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý Thuyết Lớp 12 Toán 12