Phương pháp giải các bài toán về mối quan hệ giữa hai đường thẳng
1. Vị trí tương đối giữa hai đường thẳng
Cho \(d,d'\) là các đường thẳng có VTCP lần lượt là \(\overrightarrow u ,\overrightarrow {u'} ,M \in d,M' \in d'\) . Ta có:
+) \(d \equiv d' \Leftrightarrow \overrightarrow u ,\overrightarrow {u'} ,\overrightarrow {MM'} \) đôi một cùng phương \( \Leftrightarrow \left[ {\overrightarrow u ,\overrightarrow {u'} } \right] = \left[ {\overrightarrow u ,\overrightarrow {MM'} } \right] = \overrightarrow 0 \)
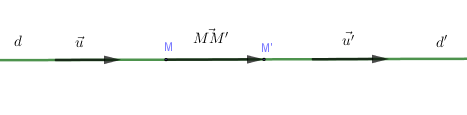
+) \(d//d' \Leftrightarrow \overrightarrow u ,\overrightarrow {u'} \) cùng phương nhưng \(\overrightarrow u ,\overrightarrow {MM'} \) không cùng phương \( \Leftrightarrow \left\{ \begin{array}{l}\left[ {\overrightarrow u ,\overrightarrow {u'} } \right] = \overrightarrow 0 \\\left[ {\overrightarrow u ,\overrightarrow {MM'} } \right] \ne \overrightarrow 0 \end{array} \right.\)
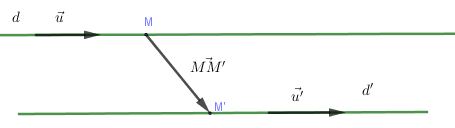
+) \(d\) cắt \(d' \Leftrightarrow \overrightarrow u ,\overrightarrow {u'} \) không cùng phương và \(\overrightarrow u ,\overrightarrow {u'} ,\overrightarrow {MM'} \) đồng phẳng \( \Leftrightarrow \left\{ \begin{array}{l}\left[ {\overrightarrow u ,\overrightarrow {u'} } \right] \ne \overrightarrow 0 \\\left[ {\overrightarrow u ,\overrightarrow {u'} } \right]\overrightarrow {MM'} = 0\end{array} \right.\)
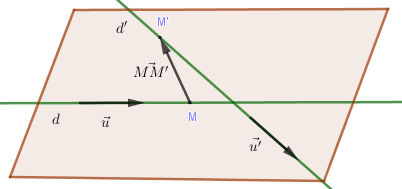
+) \(d\) chéo \(d' \Leftrightarrow \overrightarrow u ,\overrightarrow {u'} ,\overrightarrow {MM'} \) không đồng phẳng \( \Leftrightarrow \left[ {\overrightarrow u ,\overrightarrow {u'} } \right]\overrightarrow {MM'} \ne 0\)
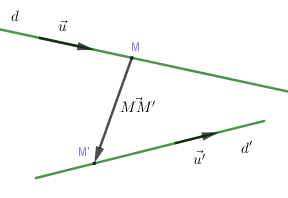
Ngoài ra, ta có thể giải hệ phương trình của hai đường thẳng để xét vị trí tương đối của hai đường thẳng:
+) Nếu hệ có nghiệm duy nhất thì \(d\) cắt \(d'\).
+) Nếu hệ vô số nghiệm thì \(d \equiv d'\).
+) Nếu hệ vô nghiệm thì:
\(d//d'\) nếu \(\overrightarrow u = k\overrightarrow {u'} \) hay \(\overrightarrow u ,\overrightarrow {u'} \) cùng phương.
\(d\) chéo \(d'\) nếu \(\overrightarrow u \ne k\overrightarrow {u'} \) hay \(\overrightarrow u ,\overrightarrow {u'} \) không cùng phương.
2. Khoảng cách và góc
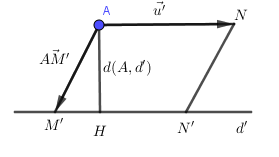
a) Khoảng cách từ điểm \(A\) đến đường thẳng \(d'\)
\(d\left( {A,d'} \right) = \dfrac{{{S_{ANN'M'}}}}{{AN}} = \dfrac{{\left| {\left[ {\overrightarrow {AM'} ,\overrightarrow {u'} } \right]} \right|}}{{\left| {\overrightarrow {u'} } \right|}}\)
b) Khoảng cách giữa hai đường thẳng:
\(d\left( {\Delta ,\Delta '} \right) = \dfrac{{\left| {\left[ {\overrightarrow u ,\overrightarrow {u'} } \right].\overrightarrow {MM'} } \right|}}{{\left| {\left[ {\overrightarrow u ,\overrightarrow {u'} } \right]} \right|}}\)
c) Góc giữa hai đường thẳng có các VTCP lần lượt là: \(\overrightarrow u ,\overrightarrow {u'} \):
$\cos \varphi = \left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right| = \dfrac{{\left| {\overrightarrow u .\overrightarrow {u'} } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow {u'} } \right|}}$
