Ta có: Đồ thị hàm số có bề lõm quay lên trên \( \Rightarrow \alpha  = 0\). Loại đáp án D.

Trục đối xứng \(x =  - \frac{b}{{2a}} < 0 \Rightarrow a.b > 0 \Rightarrow b > 0 \Rightarrow \) Loại đáp án A, C.

Đồ thị cắt trục Oy có \(y > 0 \Rightarrow c > 0\). 

Dựa vào bảng xét dấu y’ hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {2; + \infty } \right)\); nghịch biến trên khoảng (-1;0) và (0;2). 

\(\begin{array}{l}
I = \lim \frac{{2n - 3}}{{2{n^2} + 3n + 1}} = \lim \frac{{{n^2}\left( {\frac{2}{n} - \frac{3}{{{n^2}}}} \right)}}{{{n^2}\left( {2 + \frac{3}{n} + \frac{1}{{{n^2}}}} \right)}}\\
 = \lim \frac{{\frac{2}{n} - \frac{3}{{{n^2}}}}}{{2 + \frac{3}{n} + \frac{1}{{{n^2}}}}} = 0
\end{array}\)

Gọi R, I, h lần lượt là bán kính đáy, độ dài đường sinh, chiều cao của hình nón.

\(\begin{array}{l}
{S_{xq}} = \pi RI \Leftrightarrow R = \frac{{{S_{xq}}}}{{\pi I}} = \frac{{2\pi {a^2}}}{{2\pi a}} = a\\
h = \sqrt {{I^2} - {R^2}}  = \sqrt {4{a^2} - {a^2}}  = a\sqrt 3 \\
V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {a^2}a\sqrt 3  = \frac{{\pi {a^3}\sqrt 3 }}{3}
\end{array}\)

Đồ thị hàm số đi lên từ trái sang phải trong khoảng (-1;0) và \(\left( {2; + \infty } \right)\) 

⇒ Hàm số đồng biến trên khoảng (-1;0) và \(\left( {2; + \infty } \right)\)

Đồ thị hàm số đi xuống từ trái sang phải trong khoảng \(\left( { - \infty ; - 1} \right)\) và (0;2) 

⇒ Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\) và (0;2).

Thay tọa độ từng phương án thì phương tình của d chỉ có điểm M(-1;1;2) thỏa mãn vì

\(\frac{{ - 1 - 1}}{2} = \frac{{1 - 2}}{1} = \frac{2}{{ - 2}} =  - 1\) 

Điều kiện: x > 9

Ta có:

\(\begin{array}{l}
\log x + \log \left( {x - 9} \right) = 1\\
 \Leftrightarrow \log \left[ {x\left( {x - 9} \right)} \right] = 1\\
 \Leftrightarrow x\left( {x - 9} \right) = 10 \Leftrightarrow \left[ \begin{array}{l}
x =  - 1\\
x = 10
\end{array} \right.
\end{array}\) 

Kết hợp điều kiện, vậy phương trình có nghiệm x = 10.

Gọi phương trình elip là \(\left( E \right) = \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\).

Vì M(4;3) là một đỉnh của hình chữ nhật cơ sở nên a = 4; b = 3.

Vậy phương trình elip là \(\left( E \right):\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\)  

\(\begin{array}{l}
\tan x = \sqrt 3  \Leftrightarrow \tan x = \tan \frac{\pi }{3}\\
 \Leftrightarrow x = \frac{\pi }{3} + k\pi ,k \in Z
\end{array}\)

Số cách chọn 3 người bất kì trong 30 là: \(C_{30}^3\)

Áp dụng các tính chất của hình đa diện:

Mỗi cạnh là cạnh chung của đúng hai mặt.

Vậy đáp án D sai.

Mặt cầu tâm I(a;b;c), bán kính R có dạng \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2}{\left( {z - c} \right)^2} = {R^2}\).

Khi đó mặt cầu \({\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {z^2} = 9\) có tâm I(1;-3;0) và bán kính R = 3.  

Đường tròn tiếp xúc với đường thẳng d

\( \Rightarrow R = d\left( {I,d} \right) = \frac{{\left| {3 - 4\left( { - 2} \right) - 26} \right|}}{{\sqrt {9 + 16} }} = 3\) 

\(\begin{array}{l}
z = {z_1}\left( {3 - 2i} \right) + {z_2}\\
 = \left( {2 + i} \right)\left( {3 - 2i} \right) + \left( {5 - 3i} \right) = 13 - 4i\\
 \Rightarrow \overline z  = 13 + 4i
\end{array}\)

\(\begin{array}{l}
I = \int\limits_a^b {f\left( x \right)dx = F\left( b \right) - F\left( a \right)} \\
 = \frac{1}{2}\left[ {2F\left( b \right) - 2F\left( a \right)} \right] = \frac{1}{2}\left( { - 1} \right) =  - \frac{1}{2}
\end{array}\)

\({\left[ {{{\log }_3}\left( {{x^2} - 1} \right)} \right]^\prime } = \frac{{{{\left( {{x^2} - 1} \right)}^\prime }}}{{\left( {{x^2} - 1} \right)\ln 3}} = \frac{{2x}}{{\left( {{x^2} - 1} \right)\ln 3}}\)

Thời gian từ lúc hãm phanh đến dừng hẳn là:

\( - 2t + 20 = 0 \Leftrightarrow t = 10\left( s \right)\) 

Khi đó trong 15 giây ô tô chuyển động với vận tốc 20 (m/s) trong 5(s).

Quãng đường ô tô đi được trong 15 giây cuối cùng là:

\(\begin{array}{l}
S = 20.5 + \int\limits_0^{10} {\left( { - 2t + 20} \right)dt = \left. {100 + \left( { - {t^2} + 20t} \right)} \right|_0^{10}} \\
 = 100 + \left( { - 100 + 200} \right) = 200\left( m \right)
\end{array}\) 

Ta có:

\(\begin{array}{l}
\mathop {\lim }\limits_{x \to {o^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {o^ + }} \frac{{\sqrt {1 + 2x}  - 1}}{x}\\
 = \mathop {\lim }\limits_{x \to {o^ + }} \frac{{2x}}{{x\left( {\sqrt {1 + 2x}  + 1} \right)}} = \mathop {\lim }\limits_{x \to {o^ + }} \frac{2}{{\sqrt {1 + 2x}  + 1}} = 1
\end{array}\) 

Và \(\mathop {\lim }\limits_{x \to {o^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {o^ - }} \left( {3x + a - 1} \right) = a - 1\) 

Mặt khác: \(f\left( 0 \right) = a - 1\) 

Hàm số liên tục tại \(x=0\)

\(\begin{array}{l}
 \Leftrightarrow f\left( 0 \right) = \mathop {\lim }\limits_{x \to {o^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {o^ + }} f\left( x \right)\\
 \Leftrightarrow a - 1 = 1 \Leftrightarrow a = 2
\end{array}\) 

Khi quay tam giác ABC quanh AB tạo thành hình nón thì đường sinh của hình nón là cạnh BC.

Độ dài đường sinh \(l\) là:

\(BC = \frac{{AC}}{{\sin \widehat {ABC}}} = \frac{{2a}}{{\sin {{30}^0}}} = 4a\).

Xét hàm số \(f\left( x \right) = \sqrt {2x + 14}  + \sqrt {5 - x} \) xác định và liên tục trên [-7;5].

Ta có:

\(\begin{array}{l}
f'\left( x \right) = \frac{1}{{\sqrt {2x + 14} }} - \frac{1}{{2\sqrt {5 - x} }} = 0\\
 \Leftrightarrow 2\sqrt {5 - x}  = \sqrt {2x + 14} 
\end{array}\)

\( \Leftrightarrow \left\{ \begin{array}{l}
x \in \left( { - 7;5} \right)\\
4\left( {5 - x} \right) = 2x + 14
\end{array} \right. \Leftrightarrow x = 1 \in \left( { - 7;5} \right)\).

Ta có: \(\left\{ \begin{array}{l}
f\left( { - 7} \right) = 2\sqrt 3 \\
f\left( 5 \right) = 2\sqrt 6 \\
f\left( 1 \right) = 6
\end{array} \right. \Rightarrow \mathop {\min }\limits_{\left[ { - 7;5} \right]} f\left( x \right) = f\left( { - 7} \right) = 2\sqrt 3 \)    

Mặt cầu (S) có tâm I(2;0;0) và có bán kính R = 3. Khoảng cách từ tâm I đến mặt phẳng là:

\(\begin{array}{l}
d\left( {I;\left( P \right)} \right) = \sqrt {{R^2} - {r^2}}  = \sqrt {{3^2} - {{\left( {\sqrt 6 } \right)}^2}}  = \sqrt 3 \\
 \Leftrightarrow \frac{{\left| {2 + m} \right|}}{{\sqrt {{1^2} + {1^2} + {{\left( { - 1} \right)}^2}} }} = \sqrt 3  \Leftrightarrow \left| {2 + m} \right| = 3 \Leftrightarrow \left[ \begin{array}{l}
m = 1\\
m =  - 5
\end{array} \right.
\end{array}\) 

Để đồ thị hàm số \(y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)\) có điểm cực đại mà không có cực tiểu thì \(\left\{ \begin{array}{l}
a < 0\\
b \le 0
\end{array} \right.\) 

\( \Leftrightarrow  - \left( {m - 3} \right) \le 0 \Leftrightarrow m \ge 3\) 

Gọi \(z = x + yi\,\left( {x,y \in R} \right)\) được biểu diễn bởi điểm M(x;y) trong mặt phẳng tọa độ Oxy.

Ta có:

\(\begin{array}{l}
\left( {\overline z  + i} \right)\left( {z + 2} \right) = \left( {x - yi + i} \right)\left( {x + yi + 2} \right)\\
 = \left( {{x^2} + 2x + {y^2} - y} \right) + \left( {x - 2y + 2} \right)i
\end{array}\) 

Vì \(\left( {\overline z  + i} \right)\left( {z + 2} \right)\) là số thuần ảo nên ta có:

\({x^2} + 2x + {y^2} - y = 0 \Leftrightarrow {\left( {x + 1} \right)^2} + {\left( {y - \frac{1}{2}} \right)^2} = \frac{5}{4}\) 

Tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn tâm có \(I\left( { - 1;\frac{1}{2}} \right)\), bán kính bằng \(\frac{{\sqrt 5 }}{2}\).

Với trận động đất 7 độ Richte.

\(\begin{array}{l}
7 = \log A - {{\mathop{\rm logA}\nolimits} _0} \Leftrightarrow 7 = \log \frac{A}{{{A_0}}}\\
 \Leftrightarrow \frac{A}{{{A_0}}} = {10^7} \Leftrightarrow A = {10^7}.{A_0}
\end{array}\) 

Với trận động đất 5 độ Richte.

\(\begin{array}{l}
5 = \log A' - {{\mathop{\rm logA}\nolimits} _0} \Leftrightarrow 5 = \log \frac{{A'}}{{{A_0}}}\\
 \Leftrightarrow \frac{{A'}}{{{A_0}}} = {10^5} \Leftrightarrow A' = {10^5}.{A_0}
\end{array}\)

Khi đó ta được tỉ lệ:

\(\frac{A}{{A'}} = \frac{{{A_0}{{.10}^7}}}{{{A_0}{{.10}^5}}} = 100 \Leftrightarrow A = 100A'\).

Mặt phẳng (Q) có một vectơ pháp tuyến là \(\overrightarrow {{n_{\left( Q \right)}}}  = \left( {1;1;3} \right)\) 

Mặt phẳng (R) có một vectơ pháp tuyến là \(\overrightarrow {{n_{\left( R \right)}}}  = \left( {2; - 1;1} \right)\) 

Ta có: \(\left[ {{{\overrightarrow n }_{(Q)}},{{\overrightarrow n }_{(R)}}} \right] = \left( {4;5; - 3} \right)\) 

Khi đó mặt phẳng (P) đi qua A(2;1;-3) và nhận \(\left[ {{{\overrightarrow n }_{(Q)}},{{\overrightarrow n }_{(R)}}} \right] = \left( {4;5; - 3} \right)\) làm vectơ pháp tuyến.

Phương trình mặt phẳng (P) là:

\(\begin{array}{l}
4\left( {x - 2} \right) + 5\left( {y - 1} \right) - 3\left( {z + 3} \right)\\
 \Leftrightarrow 4x + 5y - 3z - 22 = 0
\end{array}\) 

Ta có \(\mathop {\lim }\limits_{x \to  + \infty } y =  - \infty \). Hệ số \(a < 0 \Rightarrow \) Loại đáp án A, D

Đồ thị hàm số cắt trục Oy tại điểm \(A\left( {0;c} \right) \Rightarrow c < 0\) 

Hàm số có 3 điểm cực trị \( \Rightarrow ab < 0 \Rightarrow b > 0\) (Vì a < 0)

⇒ Loại đáp án A, đáp án B thỏa mãn.

Ta có:

\(\begin{array}{l}
I = \int\limits_0^{\frac{\pi }{2}} {\sin 2x.f'\left( {{\mathop{\rm sinx}\nolimits} } \right)dx} \\
 = 2\int\limits_0^{\frac{\pi }{2}} {\sin x.f'\left( {\sin x} \right)\cos xdx} 
\end{array}\) 

Đặt \(t = \sin x \Rightarrow dt = \cos xdx\) 

Đổi cận: \(x = 0 \Rightarrow t = 0;\,x = \frac{\pi }{2} \Rightarrow t = 1\) 

Khi đó:

\(\begin{array}{l}
I = 2\int\limits_0^{\frac{\pi }{2}} {\sin x.f'\left( {\sin x} \right)\cos xdx} \\
 = 2\int\limits_0^1 {t.f'\left( t \right)dt = 2\int\limits_0^1 {x.f'\left( x \right)dx} } 
\end{array}\) 

Đặt: \(\left\{ \begin{array}{l}
u = x\\
dv = f'\left( x \right)dx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = dx\\
v = f\left( x \right)
\end{array} \right.\) 

Khi đó: \(I = 2\int\limits_0^1 {x.f'\left( x \right)dx = 2\left[ {\left. {x.f\left( x \right)} \right|_0^1 - \int\limits_0^1 {f\left( x \right)dx} } \right]} \) 

\( = 2\left[ {f\left( 1 \right) - \int\limits_0^1 {f\left( x \right)dx} } \right] = 2\left( {1 - \frac{1}{3}} \right) = \frac{4}{3}\) 

Có 20 cách để chọn 1 tổ trưởng từ 20 người.

Sau khi chọn 1 tổ trưởng thì có 19 cách để chọn 1 tổ phó.

Sau đó có \(C_{18}^3\) cách để chọn 3 thành viên còn lại.

Vậy có \(20.19.C_{18}^3 = 310080\) cách chọn một nhóm 5 người thỏa yêu cầu bài toán.

Theo giả thiết đề bài % cacbon 14 còn lại trong mẫu gôc là 80%.

\(\begin{array}{l}
 \Rightarrow 80 = 100.{\left( {0,5} \right)^{\frac{t}{{5750}}}} \Leftrightarrow {\left( {0,5} \right)^{\frac{t}{{5750}}}} = 0,8\\
 \Leftrightarrow \frac{t}{{5750}} = {\log _{0,5}}0,8\\
 \Leftrightarrow t = 5750.{\log _{0,5}}0,8 = 1851
\end{array}\) 

Gọi C là tâm của đáy ABCD.

Ta có: \(\left\{ \begin{array}{l}
BO \bot AC\\
BO \bot SA
\end{array} \right. \Rightarrow BO \bot \left( {SAC} \right)\) 

\( \Rightarrow SO\) là hình chiếu của SB trên (SAC).

Do đó góc giữa SB với mặt phẳng (SAC) là góc \(\widehat {BSO} = \alpha \)

Ta có: \(BO = \frac{{BD}}{2} = \frac{{a\sqrt 2 }}{2}\) 

\(SB = \sqrt {S{A^2} + A{B^2}}  = \sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {a^2}}  = 2a\) 

Xét tam giác SBO vuông tại O:

\(\sin \alpha  = \frac{{BO}}{{SB}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{2a}} = \frac{{\sqrt 2 }}{4}\) 

Xét tam giác A’AB vuông tại A:

\(AB = \sqrt {A'{B^2} - A{{A'}^2}}  = \sqrt {{{\left( {3a} \right)}^2} - {{\left( {2a} \right)}^2}}  = a\sqrt 5  = AC\) 

Diện tích tam giác ABC là:

\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}a\sqrt 5 .a\sqrt 5  = \frac{{5{a^2}}}{2}\) 

Thể tích khối lăng trụ ABC.A’B’C’ là:

\({V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = 2a.\frac{{5{a^2}}}{2} = 5{a^3}\). 

Xét cosx = 0 khi đó phương trình trở thành 1 = 0 (vô lý).

Với \(\cos x \ne 0\), chia 2 vế cho \({\cos ^2}x\), ta có:  

\(\begin{array}{l}
{\tan ^2}x - 4\tan x + 3 = 0\\
 \Leftrightarrow \left[ \begin{array}{l}
\tan x = 1\\
\tan x = 3
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
\tan x = 1\\
\cot x = \frac{1}{3}
\end{array} \right.
\end{array}\) 

Gọi I là tâm của mặt cầu (S) và H là hình chiếu của I trên (P)

Khi đó H là tâm của đường tròn (C).

Do tam giác ABC đều do đó H trọng tâm của tam giác ABC.

Đường tròn (C) có chu vi bằng \(8\pi \left( {cm} \right)\) 

Khi đó: CV = \(2\pi r \Leftrightarrow 8\pi  = 2\pi r \Leftrightarrow r = 4 = AH\) 

Ta có: \(AH = \frac{{AB\sqrt 3 }}{3} \Leftrightarrow AB = 4\sqrt 3 \) 

\( \Rightarrow {S_{ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = 12\sqrt 3 \) 

Thể tích khối tứ diện là:

\({V_{D.ABC}} = \frac{1}{3}d\left( {D;\left( {ABC} \right)} \right).{S_{ABC}} = d\left( {D;\left( {ABC} \right)} \right) = 4\sqrt 3 \) 

Do đó thể tích của tứ diện ABCD lớn nhất

⇔ khoảng cách từ D đến (ABC) là lớn nhất ⇔ H, I, D thẳng hàng

Ta có: \(IH = \sqrt {{R^2} - {r^2}}  = \sqrt {{5^2} - {4^2}}  = 3\).

Khi đó \(D{H_{\max }} = DI + IH = 5 + 3 = 8\) 

Vậy \({V_{\max }} = \frac{1}{3}d\left( {D;\left( {ABC} \right)} \right).{S_{ABC}} = \frac{1}{3}.8.12\sqrt 3  = 32\sqrt 3 \)  

Gọi A(a;0;0), B(0;b;0), C(0;0;c)

\( \Rightarrow OA = \left| a \right|\,,OB = \left| b \right|\,,OC = \left| c \right|\) 

Để O.ABC là hình chóp đều \(\left| a \right| = \left| b \right| = \left| c \right|\).

Mặt phẳng đoạn chắn đi qua các điểm A, B, C có dạng:

\(\left( P \right):\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) 

Mặt phẳng (P) đi qua điểm M nên: \(\frac{1}{a} + \frac{2}{b} + \frac{3}{c} = 1\) 

Từ đó ta có hệ phương trình: \(\left\{ \begin{array}{l}
\frac{1}{a} + \frac{2}{b} + \frac{3}{c} = 1\\
\left| a \right| = \left| b \right| = \left| c \right|
\end{array} \right.\)

Trường hợp 1: b = c = a khi đó ta được:

\(\frac{1}{a} + \frac{2}{a} + \frac{3}{a} = 1 \Leftrightarrow a = 6\) 

Phương trình mặt phẳng:

\(\left( P \right):\frac{x}{6} + \frac{y}{6} + \frac{z}{6} = 1 \Leftrightarrow x + y + z - 6 = 0\)

 \(\Rightarrow \) Đáp án A đúng.

Trường hợp 2: \(b = c =  - a\) khi đó ta được:

\(\frac{1}{a} + \frac{2}{{ - a}} + \frac{3}{{ - a}} = 1 \Rightarrow a =  - 4\) 

Phương trình mặt phẳng:

\(\left( P \right) :\frac{x}{{ - 4}} + \frac{y}{4} + \frac{z}{4} = 1 \Leftrightarrow x - y - z + 4 = 0 \)

\(\Rightarrow \) Đáp án B đúng.

Trường hợp 3: \(b =  - a\,,c = a\) khi đó ta được:

\(\frac{1}{a} + \frac{2}{{ - a}} + \frac{3}{a} = 1 \Rightarrow a = 2\) 

Phương trình mặt phẳng:

\(\left( P \right) :\frac{x}{2} + \frac{y}{{ - 2}} + \frac{z}{2} = 1 \Leftrightarrow x - y + z - 2 = 0\)

\( \Rightarrow \) Đáp án D đúng.

Trường hợp 4: \(b = a\,,c =  - a\) khi đó ta được \(\frac{1}{a} + \frac{2}{a} + \frac{3}{{ - a}} = 1 \Leftrightarrow 0 = 1\) (vô lý)

Điều kiện: \(\left\{ \begin{array}{l}
x > 0\\
x \ne \frac{1}{2}
\end{array} \right.\) 

\(\begin{array}{l}
{\log _2}\left( {\frac{{{{\left( {2x - 1} \right)}^2}}}{x}} \right) + \left( {4{x^2} - 4x + 1} \right) = 2x + 1\\
 \Leftrightarrow {\log _2}{\left( {2x - 1} \right)^2} + {\left( {2x - 1} \right)^2} - {\log _2}x = 2x + 1\\
 \Leftrightarrow {\log _2}{\left( {2x - 1} \right)^2} + {\left( {2x - 1} \right)^2} = {\log _2}2x + 2x
\end{array}\) 

Xét hàm \(f\left( t \right) = {\log _2}t + t\) trên khoảng \(\left( {0; + \infty } \right)\).

Ta có: \(f'\left( t \right) = \frac{1}{{t\ln 2}} + 1 > 0;\,\forall t > 0\) 

\( \Rightarrow f\left( t \right)\) đồng biến trên khoảng xác định.

Mà \(f\left[ {{{\left( {2x - 1} \right)}^2}} \right] = f\left( {2x} \right)\)

 \(\begin{array}{l}
 \Leftrightarrow {\left( {2x - 1} \right)^2} = 2x \Leftrightarrow 4{x^2} - 6x + 1 = 0\\
 \Leftrightarrow \left[ \begin{array}{l}
x = \frac{{3 + \sqrt 5 }}{4}\\
x = \frac{{3 - \sqrt 5 }}{4}
\end{array} \right.
\end{array}\)

Do \(\left( {{x_1} < {x_2}} \right) \Rightarrow \left\{ \begin{array}{l}
{x_1} = \frac{{3 - \sqrt 5 }}{4}\\
{x_2} = \frac{{3 + \sqrt 5 }}{4}
\end{array} \right.\).

\( \Rightarrow {x_1} + 2{x_2} = \frac{{3 - \sqrt 5 }}{4} + 2\left( {\frac{{3 + \sqrt 5 }}{4}} \right) = \frac{1}{4}\left( {9 + \sqrt 5 } \right)\)

\( \Rightarrow a = 9;\,b = 5 \Rightarrow P = a + b = 14\)  

Ta có: y’ = 12x³ – 12x² – 12x + 12.

Bảng biến thiên

=> M(-1;-10) => x₁ + y₁ = -11

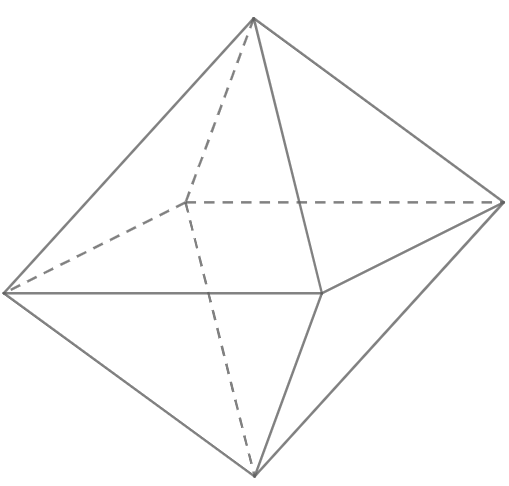
Hình bát diện đều có 12 cạnh.

Dựa vào đồ thị hàm số ta thấy hàm số có hệ số a > 0 nên loại D.

Điểm cực tiểu (1; -1) nên loại A và B.

Vậy chọn C. 

Mệnh đề đúng:

Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.

Giải tìm số điểm cực trị từng đáp án:

\(\begin{array}{l}
y' = 8{x^3} - 8x\\
y' = 0 \Leftrightarrow 8{x^3} - 8x = 0\\
 \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x =  \pm 1
\end{array} \right.
\end{array}\)

Chọn A

Chọn D.

Vì đồ thị Hình II nằm phía trên trục hoành và đi qua điểm (-1;0).

Chọn A.

y = 1 - sin²x là hàm số chẵn

\(\begin{array}{l}
\mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{7 - 2x}}{{x - 2}} =  + \infty \\
\mathop {\lim y}\limits_{x \to {2^ - }}  = \mathop {\lim }\limits_{x \to 2 - } \frac{{7 - 2x}}{{x - 2}} =  - \infty 
\end{array}\)

Vậy Đồ thị hàm số \(y=\frac{{7-2x}}{{x-2}}\) có tiệm cận đứng là đường thẳng x = 2.

Chọn A.

Hình 4 không phải là hình đa diện.

Hoành độ giao điểm của đồ thị  hàm số \(y=\frac{{2x+1}}{{x-1}}\) với đường thẳng y = 2x + 3 là nghiệm của phương trình

\(\frac{{2x+1}}{{x-1}}=2x + 3\)

Phương tình có 2 nghiệm phân biệt nên có 2 giao điểm

Chọn D.

\({u_{11}} = \frac{{{{11}^2} + 2.11 - 1}}{{11 + 1}} = \frac{{71}}{6}\)

Chọn C.

Đồ thị hình bên là của hàm số \(y=-x^4+2x^2+1\)

\(\left\{ \begin{array}{ccccc} {u_4} = {u_1} + 3d = - 12\\ u{ _{14}} = {u_1} + 13d = 18 \end{array} \right.\)

\(\Rightarrow \left\{ \begin{array}{l} {u_1} = - 21\\ d = 3 \end{array} \right.\)

\(\Rightarrow {S_{16}} = \frac{{16.\left( { - 42 + 15.3} \right)}}{2} = 24\)

Để đồ thị của hàm số \(y=2x^3-(2+m)x+m\) cắt trục hoành tại 3 điểm phân biệt thì phương trình x^3-(2+m)x+m=0 có 3 nghiệm phân biệt.

Giải ra được \(m > -\frac{1}{2}\,\,,m\ne 4\)