Hình có tâm đối xứng

HocOn247 - Học toán và các môn với bài tập, lý thuyết và đề thi đầy đủ
(397) 1324 26/09/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    I. Thế nào là hình có tâm đối xứng

    Các hình có đặc điểm:

    Mỗi hình có một điểm O, mà khi quay hình đó xung quanh điểm O đúng một nửa vòng thì hình thu được chồng khít với chính nó ở vị trí ban đầu (trước khi quay).

     Những hình như thế được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.

    Ví dụ:
    + Các hình tròn và chong chóng bốn cánh dưới đây là các hình có tâm đối xứng vì khi quay nửa vòng quanh điểm O thì hình thu được chồng khít với chính nó ở vị trí ban đầu.

    + Ta thấy hình chong chóng ba cánh khi quay nửa vòng quanh điểm O thì hình thu được không chồng khít với chính nó ở vị trí ban đầu => Hình này không có tâm đối xứng.

    II. Tâm đối xứng của một số hình phẳng

    1.

    Đoạn thẳng AB là hình có tâm đối xứng và tâm đối xứng là trung điểm M của đoạn thẳng

    Đường tròn là hình có tâm đối xứng và tâm đối xứng là tâm của nó.

    2. 

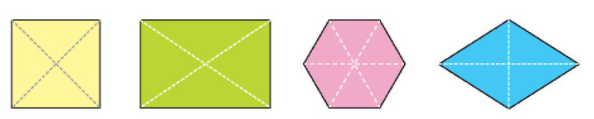
    - Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.

    - Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.

    Xem toàn bộ nội dung Toán 6 - Cánh diều:

    (397) 1324 26/09/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 6 Toán 6 - Cánh diều