Lý thuyết
Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Công thức
Công thức Toán học
Soạn văn
Toán THPT
Toán THCS
Thi vào lớp 10
Tuyển sinh
Đại học
Bản tin
Thư viện câu hỏi
Thi Online
Hỏi bàiTập hợp các số nguyên
I. Tập hợp số nguyên
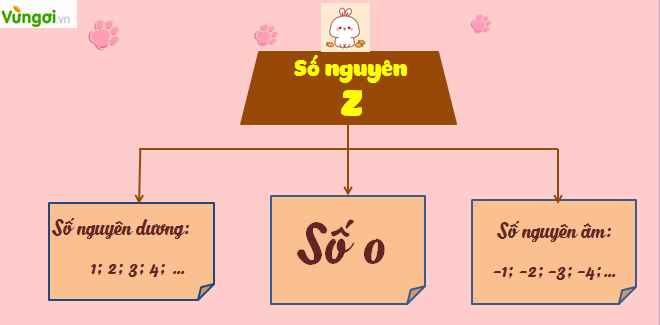
Tập hợp số gồm các số nguyên âm, số \(0\) và các số nguyên dương được gọi là tập hợp số nguyên.
Tập hợp các số nguyên được kí hiệu là \(\mathbb{Z}\).
\(\mathbb{Z} = \left\{ {...;\, - 4;\, - 3;\, - 2;\, - 1;\,\,0;\,\,1;\,\,2;\,\,3;\,\,4;...} \right\}\)
Chú ý:
Số \(0\) không là số nguyên dương, cũng không là số nguyên âm.
Ví dụ 1:
\(1;\,\,23;\,247;\, - 1;\, - 92;\,- 143\) là các số nguyên.
Ví dụ 2:
Ta có: \( - 3 \in \mathbb{Z};\,\,0 \in \mathbb{Z};\,\,25 \in \mathbb{Z}\).
II. Biểu diễn số nguyên trên trục số
1. Trục số nằm ngang
- Chiều dương hướng từ trái sang phải, chiều ngược lại là chiều âm.
- Điểm gốc của trục số là điểm \(0\).
- Điểm biểu diễn số nguyên \(a\) gọi là điểm \(a\).
- Đơn vị đo độ dài trên trục số là độ dài đoạn thẳng nối điểm \(0\) với điểm \(1\).
Ví dụ:
Trên trục số đã cho:
+ Điểm \(A\) biểu diễn số \( - 5\).
+ Điểm \(C\) biểu diễn số \( - 1\).
+ Điểm \(M\) biểu diễn số \(2\).
2. Trục số thẳng đứng
- Chiều dương hướng từ dưới lên trên, chiều ngược lại là chiều âm.
- Điểm gốc của trục số là điểm \(0\).
- Điểm biểu diễn số nguyên \(a\) gọi là điểm \(a\).
- Đơn vị đo độ dài trên trục số là độ dài đoạn thẳng nối điểm \(0\) với điểm \(1\).
Ví dụ:
Trên trục số đã cho:
+ Điểm \(A\) biểu diễn số \(2\).
+ Điểm \(B\) biểu diễn số \( - 1\).
III. Số đối của một số nguyên
Hai số nguyên trên trục số nằm ở hai phía của điểm \(0\) và cách đều điểm \(0\) được gọi là hai số đối nhau.
Chú ý:
- Số đối của một số nguyên dương là một số nguyên âm.
- Số đối của một số nguyên âm là một số nguyên dương.
- Số đối của \(0\) là \(0.\)
Ví dụ:
+ Số đối của \(3\) là \( - 3\).
+ Số đối của \( - 12\) là \(12\).
+ Số đối của 2021 là \( - 2021\).