Tam giác đều. Hình lục giác đều
I. Tam giác đều
1. Nhận biết tam giác đều
Trong tam giác đều:
+ Ba cạnh bằng nhau
+ Ba góc bằng nhau.
Ví dụ:
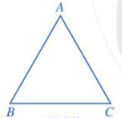
Tam giác đều \(ABC\) có:
+ Ba cạnh bằng nhau: \(AB = BC = CA\).
+ Ba góc ở các đỉnh \(A,B,\,C\) bằng nhau.
2. Vẽ tam giác đều
Cách vẽ tam giác đều cạnh \(a\,(cm)\) bằng thước và compa:
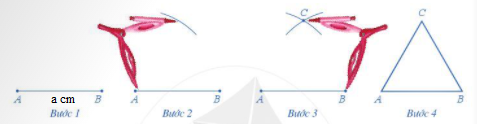
Bước 1. Dùng thước vẽ đoạn thẳng AB = a cm
Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB
Bước 3. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA; gọi C là giao
điểm của hai phần đường tròn vừa vẽ.
Bước 4. Dùng thước vẽ các đoạn thẳng AC và BC.
II. Lục giác đều
Lục giác đều \(ABCDEF\) có:
- Sáu đỉnh A, B, C, D, E, F
- Sáu cạnh bằng nhau: \(AB = BC = CD = DE = EF\).
- Sáu góc ở các đỉnh A, B, C, D, E, F bằng nhau.
- Ba đường chéo chính bằng nhau \(AD = BE = CF\).
Chú ý:
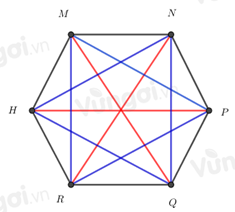
Cho hình lục giác đều \(MNPQRH\) như hình vẽ:
- MP, PR, MR, NQ, QH, HN được gọi là các đường chéo phụ của hình lục giác đều.
- Độ dài các đường chéo phụ bằng nhau.
- Các đường chéo chính cắt nhau tại 1 điểm.
- Mỗi góc của hình lục giác đều bằng \({120^0}\).
