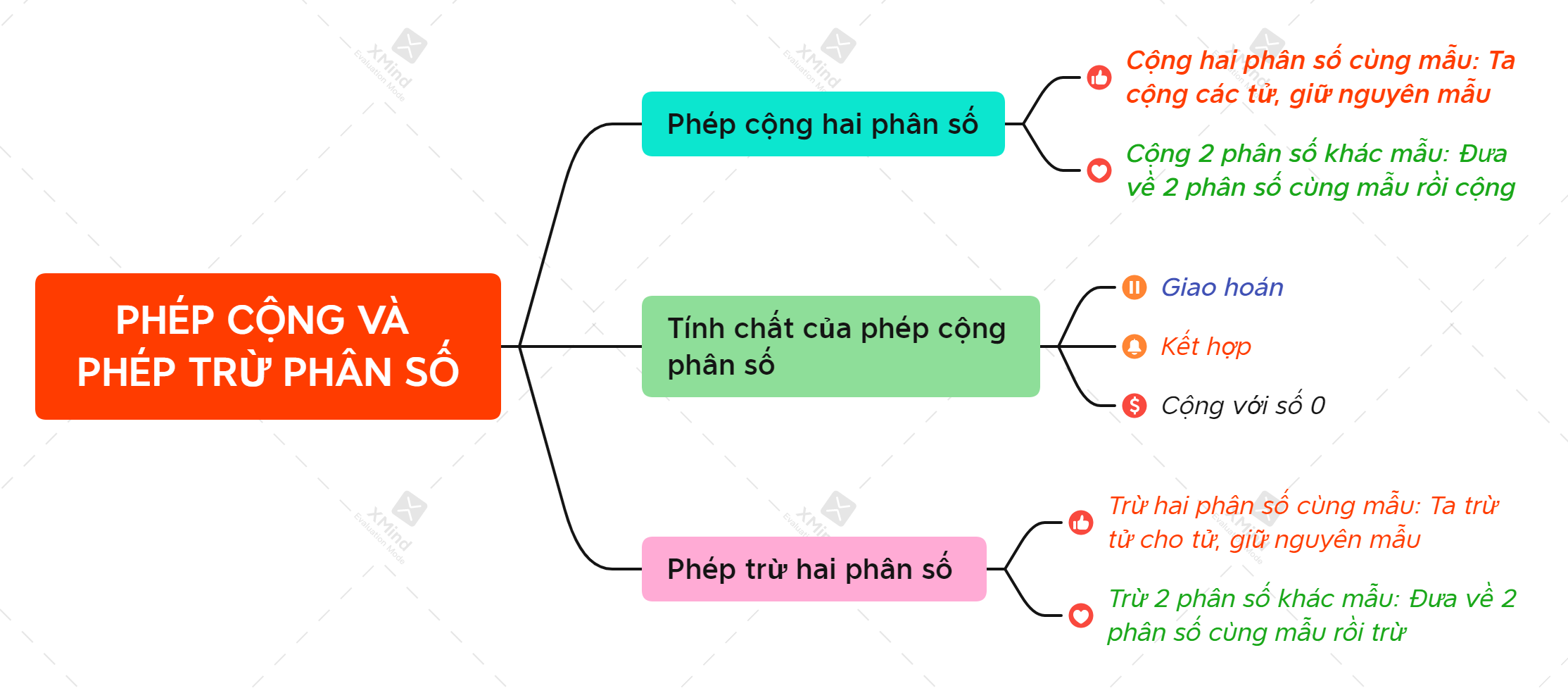
Phép cộng, phép trừ phân số

Lý thuyết về phép cộng, phép trừ phân số môn toán lớp 6 sách Cánh Diều với nhiều dạng bài cùng phương pháp giải nhanh kèm bài tập vận dụng
(398) 1325 26/09/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    I. Phép cộng hai phân số

    a) Cộng hai phân số cùng mẫu:

    Muốn cộng hai phân số cùng mẫu, ta cộng các tử và giữ nguyên mẫu.

    $\dfrac{a}{m} + \dfrac{b}{m} = \dfrac{{a + b}}{m}$ $(m \ne 0)$

    Ví dụ:

     $\dfrac{8}{5} + \dfrac{7}{5} = \dfrac{{8 + 7}}{5} = \dfrac{{15}}{5} = 3$

    b) Cộng hai phân số khác mẫu:

    Muốn cộng hai phân số khác mẫu, ta viết chúng dưới dạng hai phân số cùng mẫu rồi cộng các tử với nhau và giữ nguyên mẫu chung.

    Ví dụ:

    $\dfrac{3}{2} + \dfrac{{ - 3}}{5} = \dfrac{{15}}{{10}} + \dfrac{{ - 6}}{{10}} = \dfrac{{15 + \left( { - 6} \right)}}{{10}} = \dfrac{9}{{10}}$.

    II. Một số tính chất của phép cộng phân số

    + Tính chất giao hoán: $\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{c}{d} + \dfrac{a}{b}$

    + Tính chất kết hợp:

    $\left( {\dfrac{a}{b} + \dfrac{c}{d}} \right) + \dfrac{p}{q} = \dfrac{a}{b} + \left( {\dfrac{c}{d} + \dfrac{p}{q}} \right)$

    + Cộng với số $0$ : $\dfrac{a}{b} + 0 = 0 + \dfrac{a}{b} = \dfrac{a}{b}$

    Ví dụ:

    - Tính chất giao hoán

    $\dfrac{1}{2} + \dfrac{3}{2} = \dfrac{3}{2} + \dfrac{1}{2}$$ = \dfrac{4}{2} = 2$

    - Tính chất kết hợp:

     $\left( {\dfrac{1}{2} + \dfrac{3}{4}} \right) + \dfrac{1}{4}$$ = \dfrac{1}{2} + \left( {\dfrac{3}{4} + \dfrac{1}{4}} \right)$$ = \dfrac{1}{2} + 1 = \dfrac{3}{2}$

    - Tính chất cộng với số 0:

    $\dfrac{1}{4} + 0 = 0 + \dfrac{1}{4} = \dfrac{1}{4}$.

    III. Số đối của một phân số

    Hai số gọi là đối nhau nếu tổng của chúng bằng $0$. Kí hiệu số đối của phân số $\dfrac{a}{b}$ là $ - \dfrac{a}{b}$.

    $\dfrac{a}{b} + \left( { - \dfrac{a}{b}} \right) = 0$.

    Ví dụ:

    $\dfrac{{ - 1}}{5}$ là số đối của $\dfrac{1}{5}$, vì $\dfrac{{ - 1}}{5} + \dfrac{1}{5} = 0$.

    Chú ý: Số đối của $0$ là $0$.

    IV. Phép trừ hai phân số

    - Muốn trừ hai phân số cùng mẫu ta lấy tử của phân số thứ nhất trừ đi tử của phân số thứ hai và giữ nguyên mẫu.

    $\dfrac{a}{m} - \dfrac{b}{m} = \dfrac{{a - b}}{m}$

    - Muốn trừ hai phân số khác mẫu, ta quy đồng hai phân số, rồi trừ hai phân số đó.

    Ví dụ:

    a) $\dfrac{2}{7} - \dfrac{5}{7} = \dfrac{{2 - 5}}{7} = \dfrac{{ - 3}}{7}$

    b) $\dfrac{1}{6} - \dfrac{1}{2} = \dfrac{1}{6} + \left( { - \dfrac{1}{2}} \right) = \dfrac{1}{6} + \left( {\dfrac{{ - 3}}{6}} \right) = \dfrac{{1 + \left( { - 3} \right)}}{6} = \dfrac{{ - 2}}{6}  = \dfrac{{ - 1}}{3}.$

    Nhận xét: Muốn trừ một phân số cho một phân số, ta có thể cộng số bị trừ với số đối của số trừ.

    Ví dụ:

    $\dfrac{5}{6} - \dfrac{{ - 1}}{3} = \dfrac{5}{6} + \dfrac{1}{3} = \dfrac{5}{6} + \dfrac{2}{6} = \dfrac{7}{6}$.

    V. Sơ đồ tư duy Phép cộng và phép trừ phân trừ

    Xem toàn bộ nội dung Toán 6 - Cánh diều:

    (398) 1325 26/09/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 6 Toán 6 - Cánh diều