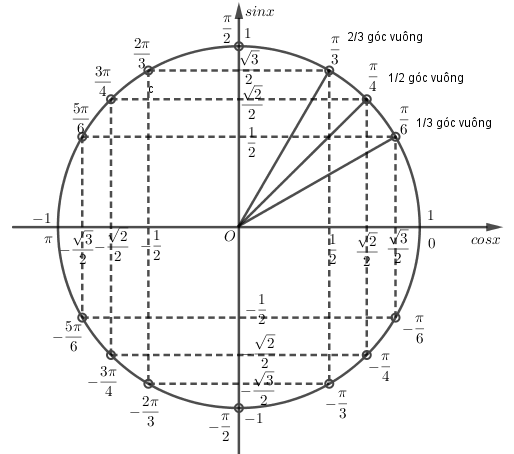
Giá trị lượng giác của một góc (cung) lượng giác

Lý thuyết về Giá trị lượng giác của một góc (cung) lượng giác MÔN TOÁN Lớp 10 với nhiều phương pháp giải nhanh kèm bài tập vận dụng
(380) 1267 29/07/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    1. Giá trị lượng giác \(\sin ,\cos ,\tan ,\cot \)

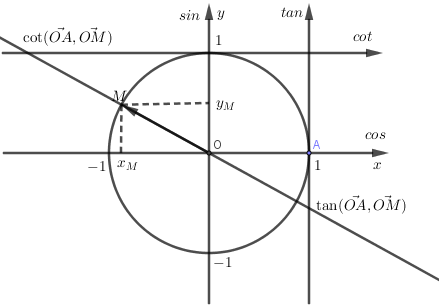
    Tính chất:

    \(\sin \alpha ,\,\cos \alpha \) xác định với mọi giá trị của \(\alpha \) và \( - 1 \le \sin \alpha  \le 1,\, - 1 \le \cos \alpha  \le 1\).

    \(\tan \alpha \) được xác định khi \(\alpha  \ne \dfrac{\pi }{2} + k\pi \), \(\cot \alpha \) xác định khi \(\alpha  \ne k\pi \)

    \(\sin \alpha  = \sin \left( {\alpha  + k2\pi } \right),\,\cos \alpha  = \cos \left( {\alpha  + k2\pi } \right)\)

    \(\tan \alpha  = \tan \left( {\alpha  + k\pi } \right),\,\cot \alpha  = \cot \left( {\alpha  + k\pi } \right)\)

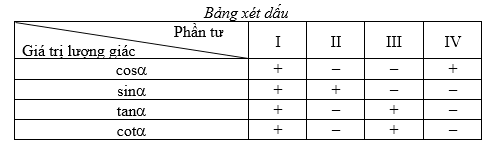
    Bảng xét dấu giá trị lượng giác của một góc, cung lượng giác

    2. Các hệ thức lượng giác cơ bản

    \(\begin{array}{l}1){\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\\2)\tan \alpha  = \dfrac{{\sin \alpha }}{{\cos \alpha }}\left( {\alpha  \ne \dfrac{\pi }{2} + k\pi } \right)\\3)\cot \alpha  = \dfrac{{\cos \alpha }}{{\sin \alpha }}\left( {\alpha  \ne k\pi } \right)\\4)1 + {\tan ^2}\alpha  = \dfrac{1}{{{{\cos }^2}\alpha }}(\alpha  \ne \dfrac{\pi }{2} + k\pi )\\5)1 + {\cot ^2}\alpha  = \dfrac{1}{{{{\sin }^2}\alpha }}(\alpha  \ne k\pi )\\6)\tan \alpha .\cot \alpha  = 1(\alpha  \ne \dfrac{{k\pi }}{2})\end{array}\)

    3. Giá trị lượng giác của các góc đặc biệt

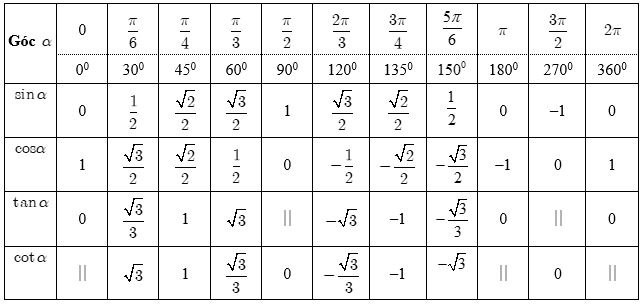
    Minh họa bằng hình vẽ:

    Xem toàn bộ nội dung Toán 10:

    (380) 1267 29/07/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 10 Toán 10