Đề thi thử THPT QG năm 2021 môn Toán - Trường THPT Thủ Đức lần 2
Đề thi thử THPT QG năm 2021 môn Toán - Trường THPT Thủ Đức lần 2
-
Hocon247
-
50 câu hỏi
-
90 phút
-
65 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Có 15 đội bóng đá thi đấu theo thể thức vòng tròn tính điểm. Hỏi cần phải tổ chức bao nhiêu trận đấu?
Ta có: Mỗi một trận đấu bóng là chọn 2 đội từ 15 độilà một tổ hợp chập 2 của 15.
Vậy số tổ hợp chập 2 của 15 là \(C_{2}^{15}\)
Cho cấp số cộng \(\left( {{u}_{n}} \right)\) có \({{u}_{1}}=5\) và \({{u}_{2}}=8\). Giá trị của \({{u}_{3}}\) bằng
Ta có: \({{u}_{1}}=5\) và \({{u}_{2}}=8\). Do \(\left( {{u}_{n}} \right)\) là cấp số cộng nên \(d={{u}_{2}}-{{u}_{1}}=8-5=3\).
Vậy \({{u}_{3}}={{u}_{2}}+d=8+3=11\)
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:
Hàm số nghịch biến trong khoảng nào?
Dựa vào bảng biến thiên, ta thấy hàm số \(y=f\left( x \right)\) đồng biến trên hai khoảng \(\left( 0;1 \right)\)
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại
Dựa vào bảng biến thiên, ta thấy hàm số đạt cực đại tại điểm x=-1.
Cho hàm số \(f\left( x \right)\) bảng xét dấu của \(f'\left( x \right)\) như sau:
.png)
Số điểm cực trị của hàm số đã cho là
Dựa vào bảng xét dấu \(f'\left( x \right)\) ta thấy \(f'\left( x \right)\) đổi dấu qua 2 điểm ⇒ Hàm số \(y=f\left( x \right)\) có 2 điểm cực trị.
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{2x + 2}}{{x - 1}}\) là:
\(\left. \begin{array}{l} \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = + \infty \\ \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = - \infty \end{array} \right\}\)Đồ thị hàm số có một đường tiệm cận đứng là x = 1
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
Dựa vào hình dáng đồ thị hàm số, ta dễ dàng nhận diện đây là đồ thị hàm số trùng phương \(y=a{{x}^{4}}+b{{x}^{2}}+c\) với a<0.
Số giao điểm của đồ thị hàm số \(y={{x}^{3}}-2{{x}^{2}}+x-12\) và trục Ox là
Xét phương trình hoành độ giao điểm: \({{x}^{3}}-2{{x}^{2}}+x-12=0\Leftrightarrow x=3\).
Vậy có 1 giao điểm của đồ thị hàm số và trục hoành.
Với a là số thực dương tùy ý, \({{\log }_{3}}\left( \frac{3}{a} \right)\) bằng:
\({\log _3}\left( {\frac{3}{a}} \right) = {\log _3}3 - {\log _3}a = 1 - {\log _3}a\)
Đạo hàm của hàm số \(y = {3^{2x + 1}}\) là
\(y' = (2x + 1)'{.3^{2x + 1}}.\ln 3 = {2.3^{2x + 1}}.\ln 3\)
Với a là số thực dương tùy ý, \(\sqrt[3]{{{a}^{4}}}\) bằng:
\(\sqrt[3]{{{a^4}}} = {a^{\frac{4}{3}}}\)
Nghiệm của phương trình \({3^{{x^2} - 3x + 1}} = \frac{1}{3}\) là:
\({3^{{x^2} - 3x + 1}} = \frac{1}{3} \Leftrightarrow {3^{{x^2} - 3x + 1}} = {3^{ - 1}} \Leftrightarrow {x^2} - 3x + 1 = - 1 \Leftrightarrow {x^2} - 3x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l} x = 1\\ x = 2 \end{array} \right.\)
Nghiệm của phương trình \({\log _3}\left( {2x - 1} \right)\) là:
\({\log _3}\left( {2x - 1} \right) = 2 \Leftrightarrow \left\{ \begin{array}{l} 2x - 1 > 0\\ 2x - 1 = {3^2} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x > \frac{1}{2}\\ x = 5 \end{array} \right. \Leftrightarrow x = 5\)
Cho hàm số \(f\left( x \right)=4{{x}^{3}}+{{e}^{x}}-1\). Trong các khẳng định sau, khẳng định nào đúng
\(\int {f(x){\rm{d}}x = \int {(4{x^3} + {e^x} - 1){\rm{d}}x = } {x^4}} + {e^x} - x + c\)
Cho hàm số \(f\left( x \right)=\sin 3x\). Trong các khẳng định sau, khẳng định nào đúng
\(\int {f(x){\rm{d}}x = \int {\sin 3x{\rm{d}}x = } - \frac{1}{3}\cos 3x} + c\)
Nếu \(\int\limits_{-1}^{4}{f\left( x \right)\text{d}x=10}\) và \(\int\limits_{-1}^{3}{f\left( x \right)\text{d}x=4}\) thì \(\int\limits_{3}^{4}{f\left( x \right)\text{d}x}\) bằng:
\(\int\limits_{ - 1}^4 {f\left( x \right){\rm{d}}x = \int\limits_{ - 1}^3 {f\left( x \right){\rm{d}}x} + \int\limits_3^4 {f\left( x \right){\rm{d}}x} \Leftrightarrow 10 = 4 + \int\limits_3^4 {f\left( x \right){\rm{d}}x} \Leftrightarrow \int\limits_3^4 {f\left( x \right){\rm{d}}x} = 10 - 4 = 6} \)
Tích phân \(\int\limits_1^3 {\left( {4{x^3} + 1} \right){\rm{d}}x} \) bằng:
\(\int\limits_1^3 {\left( {4{x^3} + 1} \right){\rm{d}}x} = \left( {{x^4} + x} \right)\left| \begin{array}{l} 3\\ 1 \end{array} \right. = \left( {{3^4} + 3} \right) - \left( {{1^4} + 1} \right) = 82\)
Số phức liên hợp của số phức \(z = 3 - 4i\) là:
\(z = 3 - 4i \Rightarrow \overline z = 3 + 4i\)
Cho hai số phức z=3-4i và \(\text{w}=5+i\). Số phức \(\text{z}\,\text{+}\,\text{w}\) là:
\(z + {\rm{w}} = 3 - 4i + 5 + i = 8 - 3i\)
Trên mặt phẳng tọa độ, điểm biểu diễn số phức 5 - 7i có tọa độ là:
Ta có: 5 - 7i có \(\left\{ \begin{array}{l} a = 5\\ b = - 7 \end{array} \right.\) suy ra điểm biểu diễn là (5;-7)
Một khối chóp có thể tích là \(36{{a}^{3}}\) và diện tích mặt đáy là \(9{{a}^{2}}\). Chiều cao của khối chóp đó bằng
\(h = \frac{{3V}}{B} = \frac{{3.36{a^3}}}{{9{a^2}}} = 12a\)
Thể tích khối lập phương có cạnh bằng 4 là
\(V = {4^3} = 64\)
Công thức tính thể tích khối trụ có chiều cao h và bán kính đáy r là:
Công thức tính thể tích khối trụ là: \(V = \pi {r^2}h\)
Một hình nón có đường kính đáy là 6cm, độ dài đường sinh là 3cm. Diện tích xung quanh của hình nón đó bằng
Bán kính đáy là 3cm.
Diện tích xung quanh của hình nón: \(S = \pi .r.l = \pi .3.3 = 9\pi \,{\rm{c}}{{\rm{m}}^{\rm{2}}}\)
Trong không gian Oxyz, cho tam giác ABC biết \(A\left( 1;-2;2 \right), B\left( 0;\,4;\,1 \right)\) và \(C\left( 2;1;-3 \right)\). Trọng tâm tam giác ABC có tọa độ là
G là trọng tâm tam giác ABC: \(\left\{ \begin{array}{l} {x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = 1\\ {y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = 1\\ {z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = 0 \end{array} \right.\)\( \Rightarrow G\left( {1;1;0} \right)\)
Trong không gian Oxyz, cho mặt cầu có phương trình \({{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y+2z-1=0\). Bán kính của mặt cầu là
Từ phương trình suy ra: tâm \(I\left( 1;-2;-1 \right)\); bán kính \(R=\sqrt{{{1}^{2}}+{{\left( -2 \right)}^{2}}+{{\left( -1 \right)}^{2}}-\left( -1 \right)}=\sqrt{7}\).
Trong không gian Oxyz, cho mặt phẳng \(\left( P \right)\) có phương trình x-2y+z-3=0. Điểm nào trong các điểm dưới đây không thuộc mặt phẳng \(\left( P \right)\)?
Thay tọa độ điểm P vào phương trình mp \(\left( P \right)\): \(1-2.1-2-3=-6\ne 0\).
Suy ra điểm P không thuộc mp \(\left( P \right)\).
Trong không gian Oxyz, cho hai điểm \(A\left( 1;2;-1 \right)\) và \(B\left( 0;2;3 \right)\). Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm A, B?
Đường thẳng AB nhận \(\overrightarrow{AB}=\left( -1;0;4 \right)\) làm VTCP.
Vectơ \(\overrightarrow{{{u}_{3}}}=\left( 1;0;-4 \right)\) cùng phương với \(\overrightarrow{AB}\) nên \(\overrightarrow{{{u}_{3}}}\) cũng là một VTCP của đường thẳng AB.
Chọn ngẫu nhiên một số tự nhiên có hai chữ số. Xác suất để chọn được một số lẻ và chia hết cho 5 bằng
Số phần tử của không gian mẫu: \(n\left( \Omega \right)=90\).
Trong 90 số tự nhiên có hai chữ số có 9 số lẻ và chia hết cho 5 là:
15;25;35;45;55;65;75;85;95
Xác suất cần tìm là: \(\frac{9}{90}=\frac{1}{10}\).
Trong các hàm số dưới đây, hàm số nào nghịch biến trên \(\mathbb{R}\)?
Loại phương án B vì hàm số có TXĐ là \(\mathbb{R}\backslash \left\{ 1 \right\}\)
Xét phương án A:
Ta có: \({y}'=-3{{x}^{2}}+6x\); \(y'=0\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=2 \\ \end{align} \right.\) nên hàm số nghịch biến trên các khoảng \(\left( -\infty ;0 \right),\left( 0;+\infty\right)\). Do đó loại phương án A.
Xét phương án C:
Ta có: \({y}'=-4{{x}^{3}}+2x\); \(y'=0\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=\pm \frac{\sqrt{2}}{2} \\ \end{align} \right.\) nên hàm số nghịch biến trên các khoảng \(\left( -\frac{\sqrt{2}}{2};0 \right),\left( \frac{\sqrt{2}}{2};+\infty \right)\). Do đó loại phương án C.
Xét phương án D:
Ta có: \({y}'=-6{{x}^{2}}+2x-1<0\,\,\forall x\in \mathbb{R}\) nên hàm số nghịch biến trên \(\mathbb{R}\). Do đó chọn phương án D.
Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right)=\frac{2x-1}{x+3}\) trên đoạn \(\left[ 0\,;\,2 \right]\). Tổng M+m bằng
Xét hàm số \(f\left( x \right)=\frac{2x-1}{x+3}\) trên đoạn \(\left[ 0\,;\,2 \right]\) .
Ta có: \(f\left( x \right)=\frac{2x-1}{x+3}\) liên tục trên đoạn \(\left[ 0\,;\,2 \right]\).
\(f\left( x \right)=\frac{2x-1}{x+3}\Rightarrow {f}'\left( x \right)=\frac{7}{{{\left( x+3 \right)}^{2}}}>0\,,\,\forall x\in \left[ 0\,;\,2 \right]\).
\(M=\underset{x\in \left[ 0\,;\,2 \right]}{\mathop{\max }}\,=f\left( 2 \right)=\frac{3}{5}, m=\underset{x\in \left[ 0\,;\,2 \right]}{\mathop{\min }}\,=f\left( 0 \right)=\frac{-1}{3}\).
Do đó, \(M+m=\frac{3}{5}-\frac{1}{3}=\frac{4}{15}\).
Tập nghiệm của bất phương trình \({\log _2}\left( {{x^2} + 3x + 2} \right) \le 1\) là
\({\log _2}\left( {{x^2} + 3x + 2} \right) \le 1 \Leftrightarrow \left\{ \begin{array}{l} {x^2} + 3x + 2 > 0\\ {x^2} + 3x + 2 \le 2 \end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l} \left[ \begin{array}{l} x > - 1\\ x < - 2 \end{array} \right.\\ - 3 \le x \le 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - 3 \le x < - 2\\ - 1 < x \le 0 \end{array} \right.\)
Cho \(\int\limits_{0}^{2}{f\left( x \right)\text{d}x=5}\). Tính tích phân \(I=\int\limits_{0}^{2}{\left[ {{x}^{2}}+2f\left( x \right) \right]\text{d}x}\).
\(I = \int\limits_0^2 {\left[ {{x^2} + 2f\left( x \right)} \right]{\rm{d}}x} = \int\limits_0^2 {{x^2}{\rm{d}}x + 2\int\limits_0^2 {f\left( x \right){\rm{d}}x} } = \frac{8}{3} + 2.5 = \frac{{38}}{3}\)
Cho số phức z=2-i. Tính môđun số phức \(\text{w}=\left( 2+i \right)\overline{z}\).
\(\text{w}=\left( 2+i \right)\overline{z} ={{\left( 2+i \right)}^{2}}=3+4i\).
\(\Rightarrow \left| \text{w} \right|=\sqrt{{{3}^{2}}+{{4}^{2}}}=5\)
Cho hình lăng trụ đều \(ABC{A}'{B}'{C}'\) có \(AB=a\,;\,A{A}'=a\sqrt{2}\) (như hình vẽ). Tính góc giữa đường thẳng \(A{C}'\) và mặt phẳng \(\left( AB{B}'{A}' \right)\).
.png)
Gọi M là trung điểm \({A}'{B}'\).
Ta có: \(\left\{ \begin{align} & {C}'M\bot {A}'{B}' \\ & {C}'M\bot A{A}' \\ \end{align} \right.\Rightarrow {C}'M\bot \left( AB{B}'{A}' \right)\). Suy ra M là hình chiếu của \({C}'\) lên mặt phẳng \(\left( AB{B}'{A}' \right)\). Do đó, AM là hình chiếu của \(A{C}'\) lên mặt phẳng \(\left( AB{B}'{A}' \right)\).
\(\Rightarrow \left( A{C}'\,,\,\left( AB{B}'{A}' \right) \right)=\left( A{C}'\,,\,AM \right)=\widehat{MA{C}'}\).
\({C}'M=\frac{a\sqrt{3}}{2}\,;\,AM=\sqrt{A{{{{A}'}}^{2}}+{A}'{{M}^{2}}}=\sqrt{2{{a}^{2}}+{{\left( \frac{a}{2} \right)}^{2}}}=\frac{3a}{2}\).
\(\tan \widehat{MA{C}'}=\frac{M{C}'}{AM}=\frac{1}{\sqrt{3}}\Rightarrow \widehat{MA{C}'}=30{}^\circ \).
Cho hình hộp chữ nhật \(ABCD{A}'{B}'{C}'{D}'\) có \(AB=3a\,;\,A{A}'=4a\) (như hình vẽ). Tính khoảng cách từ điểm B đến mặt phẳng \(\left( AD{C}'{B}' \right)\).
.png)
.png)
Dựng \(BH\bot A{B}'\,\left( 1 \right)\)
Ta có: \(\left\{ \begin{align} & {B}'{C}'\bot B{B}' \\ & {B}'{C}'\bot AB \\ \end{align} \right.\Rightarrow {B}'{C}'\bot \left( AB{B}'{A}' \right)\Rightarrow {B}'{C}'\bot BH\,\left( 2 \right)\)
Từ (1) và (2) suy ra: \(BH\bot \left( AD{C}'{B}' \right)\)
\(\Rightarrow d\left( B\,;\,\left( AD{C}'{B}' \right) \right)=BH=\frac{B{B}'.AB}{\sqrt{B{{{{B}'}}^{2}}+A{{B}^{2}}}}$$=\frac{4a.3a}{\sqrt{{{\left( 4a \right)}^{2}}+{{\left( 3a \right)}^{2}}}}=\frac{12a}{5}\).
Trong không gian với hệ trục tọa độ Oxyz. Hãy viết phương trình mặt cầu có tâm \(I\left( 2\,;\,2\,;\,3 \right)\) và tiếp xúc với mặt phẳng \(\left( Oxz \right)\).
Mặt cầu có tâm \(I\left( 2\,;\,2\,;\,3 \right)\) và tiếp xúc với mặt phẳng \(\left( Oxz \right)\) nên có bán kính \(R=d\left( I\,,\,\left( Oxz \right) \right)=2\).
Suy ra phương trình mặt cầu: \({{\left( x-2 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=4\).
Trong không gian với hệ trục tọa độ Oxyz. Hãy viết phương trình chính tắc của đường thẳng qua \(A\left( 2\,;\,1\,;\,-1 \right)\) và vuông góc với mặt phẳng \(\left( \alpha \right):2x+y-z+5=0\)
Đường thẳng qua \(A\left( 2\,;\,1\,;\,-1 \right)\) và vuông góc với mặt phẳng \(\left( \alpha\right):2x+y-z+5=0\) có VTCP \(\overrightarrow{u}=\overrightarrow{{{n}_{\left( P \right)}}}=\left( 2\,;\,1\,;\,-1 \right)\) nên có phương trình chính tắc: \(\frac{x-2}{-2}=\frac{y-1}{-1}=\frac{z+1}{1}\).
Cho hàm số \(f\left( x \right)\), đồ thị của hàm số \(y=f'\left( x \right)\) là đường cong trong hình bên. Giá trị lớn nhất của hàm số \(g\left( x \right)=f\left( x+2 \right)-x\) trên đoạn \(\left[ -3\,;\,0 \right]\) bằng
Xét hàm số \(g\left( x \right)=f\left( x+2 \right)-x\) trên đoạn \(\left[ -3\,;\,0 \right]\).
Đặt \(x+2=t\Rightarrow y=g\left( t \right)=f\left( t \right)-t+2\)
\(x\in \left[ -3\,;\,0 \right]\Rightarrow t\in \left[ -1\,;\,2 \right]\)
\(\Rightarrow {y}'={f}'\left( t \right)-1=0\Leftrightarrow {f}'\left( t \right)=1\left( * \right)\)
Ta thấy, dựa vào đồ thị hàm số thì phương trình \(\left( * \right)\) có 2 nghiệm phân biệt t=0 và t=1 nằm
trong \(\left[ -1\,;\,2 \right]\)
Ta có BBT:
\(\Rightarrow \underset{\left[ -1\,;\,2 \right]}{\mathop{\max }}\,\left[ f\left( t \right)-t+2 \right]=f\left( 1 \right)+1\).
Gọi S là tập hợp tất cả các số nguyên m để phương trình \({{\log }_{\sqrt{2}}}\left( x-2 \right)-{{\log }_{2}}\left( mx-16 \right)=0\) có hai nghiệm thực phân biệt. Tính tổng các phần tử của S
Điều kiện x>2 và mx-16>0.
Khi đó \({{\log }_{\sqrt{2}}}\left( x-2 \right)-{{\log }_{2}}\left( mx-16 \right)=0\) tương đương với \({{\log }_{2}}{{\left( x-2 \right)}^{2}}={{\log }_{2}}\left( mx-16 \right)\)
Hay \(f\left( x \right)={{x}^{2}}-\left( m+4 \right)x+20=0\,\,\,\left( 1 \right).\)
Yêu cầu bài toán trở thành tìm tập hợp các giá trị nguyên của tham số m để phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt lớn hơn 2 .
Hay \(\left\{ \begin{array}{l} \Delta = {\left( {m + 4} \right)^2} - 80 > 0\\ f\left( 2 \right) = 16 - 2m > 0\\ \frac{S}{2} = \frac{{m + 4}}{2} > 2 \end{array} \right. \Leftrightarrow - \,4 + \,4\sqrt 5 < m < 8.\)
Suy ra \(m \in \left\{ {5,6,7} \right\}.\)
Vậy tổng các phần tử của S bằng 18.
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {{x^2} - 2}&{{\rm{ khi }}x \ge 3}\\ {2x + 1}&{{\rm{ khi }}x < 3} \end{array}} \right.\). Tích phân \(\int\limits_0^{\frac{\pi }{4}} {\frac{{f\left( {3\tan x + 1} \right)}}{{{{\cos }^2}x}}\;dx} \) bằng
Đặt \(I=\int\limits_{0}^{\frac{\pi }{4}}{\frac{f\left( 3\tan x+1 \right)}{{{\cos }^{2}}x}~dx}\)
Đặt \(u=3\tan x+1\Rightarrow du=3.\frac{dx}{{{\cos }^{2}}x}\)
Đổi cận \(x=0\Rightarrow t=1;x=\frac{\pi }{4}\Rightarrow t=4.\)
Do đó \(I=\frac{1}{3}\int\limits_{1}^{4}{f\left( u \right)du=\frac{1}{3}\int\limits_{1}^{4}{f\left( x \right)dx}}=\frac{1}{3}\left[ \int\limits_{1}^{3}{\left( 2x+1 \right)du}+\int\limits_{3}^{4}{\left( {{x}^{2}}-2 \right)dx} \right]=\frac{1}{3}\left( 10+\frac{31}{3} \right)=\frac{61}{9}\)
Có bao nhiêu số phức z thỏa mãn điều kiện \(\left| z-3i \right|=5\) và \(\frac{z}{z-4}\) là số thuần ảo?
Giả sử \(z=x+yi\ \left( x,y\in \mathbb{R} \right)\) có điểm biểu diễn là \(M\left( x\,;\,y \right)\)
Ta có \(\left| z-3i \right|=5\Rightarrow {{x}^{2}}+{{\left( y-3 \right)}^{2}}=25\Rightarrow M\in \left( C \right)\): tâm \(I\left( 0;3 \right)\), bán kính R=5
Ta lại có \(\frac{z}{z-4}=\frac{x+yi}{\left( x-4 \right)+yi}=\frac{\left( x+yi \right)\left[ \left( x-4 \right)-yi \right]}{{{\left( x-4 \right)}^{2}}+{{y}^{2}}}=\frac{x\left( x-4 \right)+{{y}^{2}}}{{{\left( x-4 \right)}^{2}}+{{y}^{2}}}+\frac{-xy+\left( x-4 \right)y}{{{\left( x-4 \right)}^{2}}+{{y}^{2}}}i\) .
Do đó \(\frac{z}{z-4}\) là số thuần ảo \(\Leftrightarrow \left\{ \begin{align} & {{x}^{2}}+{{y}^{2}}-4x=0 \\ & \left( x;y \right)\ne \left( 4;0 \right) \\ \end{align} \right.\)
⇒ \(M \in(C')\): với tâm \(K\left( 2;0 \right)\), bán kính \(R'=2,M\ne N\left( 4\,;\,0 \right).\)
Ta có \(R-R'<IK=\sqrt{13}<R+R'\) suy ra hai đường tròn \(\left( C \right)\) và \(\left( C' \right)\) cắt nhau tại 2 điểm phân biệt.
Lại có điểm \(N\left( 0\,;\,4 \right)\) đều thuộc hai đường tròn
Vậy có 1 số phức z thỏa yêu cầu bài toán.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và \(SA\bot \left( ABCD \right),\) góc giữa SA và mặt phẳng \(\left( SBD \right)\) bằng \({{30}^{{}^\circ }}\). Thể tích của khối chóp S.ABCD bằng
.png)
Gọi \(O=AC\cap BD,\) kẻ \(AH\bot SO\left( H\in SO \right).\)
Ta có \(\left. \begin{align} & BD\bot AC \\ & BD\bot SA \\ \end{align} \right\}\Rightarrow BD\bot \left( SAC \right)\Rightarrow BD\bot AH\Rightarrow AH\bot \left( SBD \right).\)
\(\Rightarrow SH\) là hình chiếu vuông góc từ SA xuống \(\left( SBD \right).\)
\(\Rightarrow \left( \widehat{SA,\left( SBD \right)} \right)=\left( \widehat{SA,SH} \right)=\widehat{ASH}=\widehat{ASO}={{30}^{\circ }}. \Rightarrow SA=\cot {{30}^{\circ }}.OA=\frac{a\sqrt{6}}{2}.\)
\(\Rightarrow {{V}_{S.ABCD}}=\frac{1}{3}SA.{{S}_{ABCD}}=\frac{1}{3}\cdot \frac{a\sqrt{6}}{2}\cdot {{a}^{2}}=\frac{{{a}^{3}}\sqrt{6}}{6}.\)
Một sân chơi cho trẻ em hình chữ nhật có chiều dài 100 m và chiều rộng là 60 m người ta làm một con đường nằm trong sân (tham khảo hình bên). Biết rằng viền ngoài và viền trong của con đường là hai đường elip, elip của đường viền ngoài có trục lớn và trục bé lần lượt song song với các cạnh hình chữ nhật và chiều rộng của mặt đường là 2 m. Kinh phí cho mỗi m2 làm đường 600 000 đồng. Tính tổng số tiền (làm tròn đến hàng nghìn) làm con đường đó.
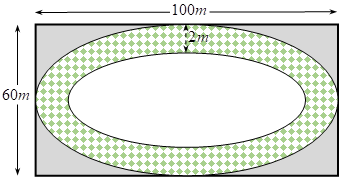
Gắn hệ trục tọa độ Oxy: đặt gốc tọa độ O vào tâm của hình elip và hai trục tọa độ song song với các cạnh của hình chữ nhật.
+ Phương trình Elip của đường viền ngoài của con đường là \(\left( {{E}_{1}} \right):\frac{{{x}^{2}}}{{{50}^{2}}}+\frac{{{y}^{2}}}{{{30}^{2}}}=1\) Phần đồ thị của \(\left( {{E}_{1}} \right)\) nằm phía trên trục hoành có phương trình \(y=30\sqrt{1-\frac{{{x}^{2}}}{{{50}^{2}}}}={{f}_{1}}\left( x \right)\).
+ Phương trình Elip của đường viền trong của con đường là \(\left( {{E}_{2}} \right):\frac{{{x}^{2}}}{{{48}^{2}}}+\frac{{{y}^{2}}}{{{28}^{2}}}=1\). Phần đồ thị của \(\left( {{E}_{2}} \right)\) nằm phía trên trục hoành có phương trình \(y=28\sqrt{1-\frac{{{x}^{2}}}{{{48}^{2}}}}={{f}_{2}}\left( x \right)\)
+Gọi \({{S}_{1}}\) là diện tích của \(\left( {{E}_{1}} \right)\) và \({{S}_{2}}\) là diện tích của \(\left( {{E}_{2}} \right).\)
Gọi S là diện tích con đường. Khi đó
\(S={{S}_{1}}-{{S}_{2}}=2\int\limits_{-50}^{50}{30\sqrt{1-\frac{{{x}^{2}}}{{{50}^{2}}}}\text{d}x}-2\int\limits_{-48}^{48}{28\sqrt{1-\frac{{{x}^{2}}}{{{48}^{2}}}}\text{d}x}\)
Tính tích phân \(I=2\int\limits_{-a}^{a}{b\sqrt{1-\frac{{{x}^{2}}}{{{a}^{2}}}}\text{d}x},\left( a,b\in {{\mathbb{R}}^{+}} \right)\)
Đặt \(x=a\sin t,\left( -\frac{\pi }{2}\le t\le \frac{\pi }{2} \right)\Rightarrow \text{d}x=a\cos t\text{d}t\).
Đổi cận \(x=-a\Rightarrow t=-\frac{\pi }{2};x=a\Rightarrow t=\frac{\pi }{2}.\)
Khi đó \(I=2\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{b\sqrt{1-{{\sin }^{2}}t}.a\cos t\,\text{d}t}=2ab\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{{{\cos }^{2}}t\,\text{d}t}=ab\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{\left( 1+\cos 2t \right)\text{d}t}\)
\(=ab\left. \left( t+\frac{\sin 2t}{2} \right) \right|_{-\frac{\pi }{2}}^{\frac{\pi }{2}}=ab\pi \)
Do đó \(S={{S}_{1}}-{{S}_{2}}=50.30\pi -48.28\pi =156\pi \)
Vậy tổng số tiền làm con đường đó là \(600000.S=600000.156\pi \approx 294053000\) đồng.
Trong không gian Oxyz, cho điểm \(A(1\,;\,-1\,;\,3)\) và hai đường thẳng \({{d}_{1}}:\frac{x-4}{1}=\frac{y+2}{4}=\frac{z-1}{-2}, {{d}_{2}}:\frac{x-2}{1}=\frac{y+1}{-1}=\frac{z-1}{1}\). Viết phương trình đường thẳng d đi qua A,vuông góc với đường thẳng \({{d}_{1}}\) và cắt đường thẳng \({{d}_{2}}\).
Ta có \({{\vec{u}}_{{{d}_{1}}}}=\left( 1;4;-2 \right)\) là vectơ chỉ phương của \({{d}_{1}}.\)
Gọi \(M=d\cap {{d}_{2}}\Rightarrow M\left( 2+t\,;\,-1-t\,;\,1+t \right)\Rightarrow \overrightarrow{AM}=\left( 1+t\,;\,-t\,;\,t-2 \right).\)
Theo đề bài d vuông góc \({{d}_{1}}\Rightarrow {{\vec{u}}_{{{d}_{1}}}}.\overrightarrow{AM}=0\Leftrightarrow 1.\left( 1+t \right)+4\left( -t \right)-2\left( t-2 \right)=0\Leftrightarrow t=1.\)
\(\Rightarrow {{\vec{u}}_{d}}=\overrightarrow{AM}=\left( 2\,;\,-1\,;\,-1 \right)\) là vectơ chỉ phương của d.
Vậy phương trình đường thẳng d: \(\frac{x-1}{2}=\frac{y+1}{-1}=\frac{z-3}{-1}.\)
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) có \(f\left( 0 \right)=1\) và đồ thị hàm số \(y=f'\left( x \right)\) như hình vẽ.
.jpg.png)
Hàm số \(y=\left| f\left( 3x \right)-9{{x}^{3}}-1 \right|\) đồng biến trên khoảng
Đặt
\(\begin{array}{l} g\left( x \right) = f\left( {3x} \right) - 9{x^3} - 1\\ \Rightarrow g'\left( x \right) = 3f'\left( {3x} \right) - 27{x^2}\\ g'\left( x \right) = 0 \Leftrightarrow f'\left( {3x} \right) = {\left( {3x} \right)^2}\left( * \right) \end{array}\)
Trên cùng một mặt phẳng tọa độ, ta vẽ đồ thị hàm số \(y=f'\left( x \right)\) và \(y={{x}^{2}}\) như hình bên.
.jpg.png)
Từ đồ thị hàm số ta có \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l} 3x = 0\\ 3x = 1\\ 3x = 2 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = \frac{1}{3}\\ x = \frac{2}{3} \end{array} \right.\)
Khi đó \(g'\left( x \right)>0\Leftrightarrow f'\left( 3x \right)>{{\left( 3x \right)}^{2}}\Leftrightarrow 0<x<\frac{2}{3}\)
\(\Rightarrow g'\left( x \right)<0\) trên \(\left( -\infty ;0 \right);\left( \frac{2}{3};+\infty \right)\)
Ta có \(g\left( 0 \right)=f\left( 0 \right)-{{9.0}^{3}}-1=0\)
Bảng biến thiên của hàm số \(y=g\left( x \right)\)
.png)
Từ bảng biến thiên ta có hàm số \(y=\left| g\left( x \right) \right|\) đồng biến trên \(\left( 0;\frac{2}{3} \right)\).
Có bao nhiêu số nguyên dương y để tập nghiệm của bất phương trình \(\left( {{\log }_{2}}x-\sqrt{2} \right)\left( {{\log }_{2}}x-y \right)<0\) chứa tối đa 1000 số nguyên
TH1. Nếu \(y=\sqrt{2}\notin \mathbb{Z}\)
TH2. Nếu \(y>\sqrt{2}\Rightarrow \left( {{\log }_{2}}x-\sqrt{2} \right)\left( {{\log }_{2}}x-y \right)\Leftrightarrow {{2}^{\sqrt{2}}}<x<{{2}^{y}}\). Tập nghiệm của BPT chứa tối đa 1000 số nguyên \(\left\{ 3;4;...;1002 \right\}\Leftrightarrow {{2}^{y}}\le 1003\Leftrightarrow y\le {{\log }_{2}}1003\approx 9,97\Rightarrow y\in \left\{ 2;...;9 \right\}\) có 8 giá trị
TH3. Nếu \(y<\sqrt{2}\Rightarrow y=1\Rightarrow \left( {{\log }_{2}}x-\sqrt{2} \right)\left( {{\log }_{2}}x-y \right)<0\Leftrightarrow 1<{{\log }_{2}}x<\sqrt{2}\Leftrightarrow 2<x<{{2}^{\sqrt{2}}}\). Tập nghiệm không chứa số nguyên nào.
Cho hàm số bậc ba \(y=f\left( x \right)\) có đồ thị như hình vẽ, biết \(f\left( x \right)\) đạt cực tiểu tại điểm x=1 và thỏa mãn \(\left[ f\left( x \right)+1 \right]\) và \(\left[ f\left( x \right)-1 \right]\) lần lượt chia hết cho \({{\left( x-1 \right)}^{2}}\) và \({{\left( x+1 \right)}^{2}}\). Gọi \({{S}_{1}},{{S}_{2}}\) lần lượt là diện tích như trong hình bên. Tính \(2{{S}_{2}}+8{{S}_{1}}\).
.jpg.png)
Đặt \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) theo giả thiết có \(\left\{ {\begin{array}{*{20}{l}} {f\left( x \right) + 1 = a{{\left( {x - 1} \right)}^2}\left( {x + m} \right)}\\ {f\left( x \right) - 1 = a{{\left( {x + 1} \right)}^2}\left( {x + n} \right)} \end{array}} \right.\)
Do đó \(\left\{ {\begin{array}{*{20}{l}} {f\left( 1 \right) + 1 = 0}\\ {f\left( { - 1} \right) - 1 = 0}\\ {f\left( 0 \right) = 0}\\ {f'\left( 1 \right) = 0} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {a + b + c + d + 1 = 0}\\ { - a + b - c + d - 1 = 0}\\ {d = 0}\\ {3a + 2b + c = 0} \end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {a = \frac{1}{2}}\\ {b = 0}\\ {c = - \frac{3}{2}}\\ {d = 0} \end{array}} \right. \Rightarrow f\left( x \right) = \frac{1}{2}{x^3} - \frac{3}{2}x} \right.\)
Ta có \(f\left( x \right) = \frac{1}{2}{x^3} - \frac{3}{2}x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x = 0}\\ {x = \pm \sqrt 3 } \end{array}} \right.\)
S1 là diện tích giới hạn bởi đồ thị \(y=\frac{1}{2}{{x}^{3}}-\frac{3}{2}x,y=-1, x=0,x=1\Rightarrow {{S}_{1}}=\int\limits_{0}^{1}{\left| \frac{1}{2}{{x}^{3}}-\frac{3}{2}x+1 \right|=\frac{3}{8}}\left( 1 \right)\)
\({{S}_{2}}\) là diện tích giới hạn bởi đồ thị \(y=\frac{1}{3}{{x}^{2}}-\frac{3}{2}x, y=0,x=1,x=\sqrt{3} \Rightarrow {{S}_{2}}=\int\limits_{1}^{\sqrt{3}}{\left| \frac{1}{2}{{x}^{3}}-\frac{3}{2}x \right|=\frac{1}{2}}\left( 2 \right)\)
Từ \(\left( 1 \right),\left( 2 \right)\Rightarrow 2{{S}_{2}}+8{{S}_{1}}=2.\frac{1}{2}+8.\frac{3}{8}=4\).
Cho số phức \({{z}_{1}}, {{z}_{2}}\) thỏa mãn \(\left| {{z}_{1}} \right|=12\) và \(\left| {{z}_{2}}-3-4\text{i} \right|=5\). Giá trị nhỏ nhất của \(\left| {{z}_{1}}-{{z}_{2}} \right|\) là
Gọi \({{z}_{1}}={{x}_{1}}+{{y}_{1}}\text{i}\) và \({{z}_{2}}={{x}_{2}}+{{y}_{2}}\text{i}\), trong đó \({{x}_{1}}, {{y}_{1}}, {{x}_{2}}, {{y}_{2}}\in \mathbb{R}\); đồng thời \({{M}_{1}}\left( {{x}_{1}};{{y}_{1}} \right)\) và \({{M}_{2}}\left( {{x}_{2}};{{y}_{2}} \right)\) lần lượt là điểm biểu diễn các số phức \({{z}_{1}}, {{z}_{2}}\).
Theo giả thiết, ta có \(\left\{ \begin{align} & x_{1}^{2}+y_{1}^{2}=144 \\ & {{\left( {{x}_{2}}-3 \right)}^{2}}+{{\left( {{y}_{2}}-4 \right)}^{2}}=25 \\ \end{align} \right.\).
Do đó \({{M}_{1}}\) thuộc đường tròn \(\left( {{C}_{1}} \right)\) có tâm \(O\left( 0;0 \right)\) và bán kính \({{R}_{1}}=12, {{M}_{2}}\) thuộc đường tròn \(\left( {{C}_{2}} \right)\) có tâm \(I\left( 3;4 \right)\) và bán kính \({{R}_{2}}=5\).
Mặt khác, ta có \(\left\{ \begin{align} & O\in \left( {{C}_{2}} \right) \\ & OI=5<7={{R}_{1}}-{{R}_{2}} \\ \end{align} \right.\) nên \(\left( {{C}_{2}} \right)\) chứa trong \(\left( {{C}_{1}} \right)\).
.png)
Khi đó \(\left| {{z}_{1}}-{{z}_{2}} \right|={{M}_{1}}{{M}_{2}}\). Suy ra \({{\left| {{z}_{1}}-{{z}_{2}} \right|}_{\min }}\Leftrightarrow {{\left( {{M}_{1}}{{M}_{2}} \right)}_{\min }}\Leftrightarrow {{M}_{1}}{{M}_{2}}={{R}_{1}}-2{{R}_{2}}=2\).
Một người thợ có một khối đá hình trụ. Kẻ hai đường kính MN,PQ của hai đáy sao cho \(MN\bot PQ.\) Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm M,N,P,Q để thu được khối đá có hình tứ diện MNPQ. Biết rằng MN=60 cm và thể tích khối tứ diện MNPQ bằng \(36d{{m}^{3}}.\) Tìm thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập phân).
Dựng hình lăng trụ MP'NQ'.M'PN'Q (như hình vẽ)
Khi đó, ta có
\({V_{MNPQ}} = {V_{MP'NQ'.M'PN'Q}} - \left( {{V_{P.MNP'}} + {V_{Q.MNQ'}} + {V_{M.M'PQ}} + {V_{N.N'PQ}}} \right) = {V_{MP'NQ'.N'PN'Q}} - 4.{V_{P.MNP'}}\)
\(\begin{array}{l} = {V_{MP'NQ'.PN'Q}} - 4.\frac{1}{2}{V_{P.MQ'NP'}} = {V_{MP'NQ'.M'PN'Q}} - 2{V_{P.MQ'NP'}}\\ = {V_{MP'NQ'.PN'Q}} - 2.\frac{1}{3}{V_{MP'NQ'.PN'Q}}\\ = \frac{1}{3}{V_{MP'NQ'.PN'Q}}. \end{array}\)
\( \Rightarrow \frac{1}{3}{V_{MP'NQ'.PN'Q}} = 36(d{m^3}) \Leftrightarrow {V_{MP'NQ'.PN'Q}} = 108\left( {d{m^3}} \right)\)
Do \(MN \bot PQ,PQ//P'Q'\) nên \(MN \bot P'Q' \Rightarrow MP'NQ'\) là hình vuông
Ta có \(MN = 60cm \Rightarrow \left\{ \begin{array}{l} MQ = \frac{{60}}{{\sqrt 2 }} = 30\sqrt 2 (cm) = 3\sqrt 2 (dm)\\ OM = \frac{{60}}{2} = 30(cm) = 3(dm) \end{array} \right.\)
\( \Rightarrow {S_{MP'NQ'}} = {\left( {3\sqrt 2 } \right)^2} = 18(d{m^2})\)
\({V_{MP'NQ'.PN'Q}} = {S_{MP'NQ'}}.h \Rightarrow 18h = 108 \Leftrightarrow h = 6(dm)\)
Thể tích khối trụ là \(V = \pi {R^2}h = \pi .O{M^2}h = \pi {.3^2}.6 = 54\pi (d{m^3})\)
Thể tích của lượng đá bị cắt bỏ là \(54\pi - 36 \approx 133,6\left( {d{m^3}} \right).\)

.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)



