Góc giữa đường thẳng và mặt phẳng

Lý thuyết về góc giữa đường thẳng và mặt phẳng môn toán lớp 11 với nhiều dạng bài cùng phương pháp giải nhanh kèm bài tập vận dụng
(403) 1344 29/07/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    1. Kiến thức cần nhớ

    Định nghĩa:

    - Nếu đường thẳng \(a\) vuông góc với mặt phẳng \(\left( P \right)\) thì ta nói góc giữa đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) bằng \({90^0}\).

    - Nếu đường thẳng \(a\) không vuông góc với mặt phẳng \(\left( P \right)\) thì góc giữa \(a\) và hình chiếu \(a'\) của nó trên \(\left( P \right)\) gọi là góc giữa đường thẳng \(a\) và mặt phẳng \(\left( P \right)\).

    Kí hiệu:

    Nếu $a \bot \left( P \right)$  thì \(\widehat {\left( {a,\left( P \right)} \right)} = {90^0}\)

    Nếu $a$ không vuông góc với $(P)$ thì \(\widehat {\left( {a,\left( P \right)} \right)} = \widehat {\left( {a,a'} \right)}\) với $a'$ là hình chiếu của $a$ trên $\left( P \right)$.

    Chú ý: \({0^0} \le \widehat {\left( {a,\left( P \right)} \right)} \le {90^0}\)

    2. Bài toán góc giữa đường thẳng và mặt phẳng

    Phương pháp:

    góc giữa đường thẳng và mặt phẳng

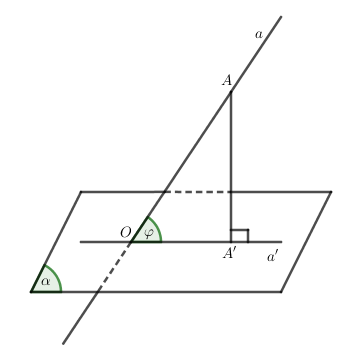
    Để xác định góc giữa đường thẳng $a$ và mặt phẳng $\left( \alpha  \right)$ ta thực hiện theo các bước sau:

    - Tìm giao điểm $O = a \cap \left( \alpha  \right)$

    - Dựng hình chiếu $A'$ của một điểm $A \in a$ xuống $\left( \alpha  \right)$

    - Góc \(\widehat {AOA'} = \varphi \) chính là góc giữa đường thẳng $a$ và $\left( \alpha  \right)$.

    *) Để dựng hình chiếu $A'$ của điểm $A$ trên $\left( \alpha  \right)$ ta chọn một đường thẳng $b \bot \left( \alpha  \right)$ khi đó $AA'//b$.

    - Để tính góc $\varphi $ ta sử dụng hệ thức lượng trong tam giác vuông $\Delta OAA'$.

    Ngoài ra, nếu không xác định góc $\varphi $ thì ta có thể tính góc giữa đường thẳng $a$ và mặt phẳng $\left( \alpha  \right)$ theo công thức $\sin \varphi  = \dfrac{{\left| {\overrightarrow u .\overrightarrow n } \right|}}{{\left| {\overrightarrow u } \right|\left| {\overrightarrow n } \right|}}$ trong đó $\overrightarrow u $ là VTCP của $a$ còn $\overrightarrow n $ là vec tơ có giá vuông góc với $\left( \alpha  \right)$.

    Xem toàn bộ nội dung Toán 11:

    (403) 1344 29/07/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 11 Toán 11