Hình lăng trụ, hình hộp, hình chóp cụt

Lý thuyết về hình lăng trụ, hình hộp, hình chóp cụt môn toán lớp 11 với nhiều dạng bài cùng phương pháp giải nhanh kèm bài tập vận dụng
(394) 1313 29/07/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    1. Hình lăng trụ và hình hộp

    a) Hình lăng trụ

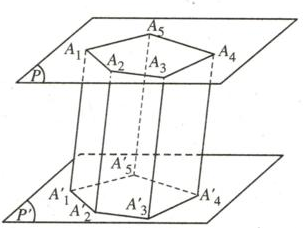
    Hình vẽ trên cho ta một hình lăng trụ, ở đó:

    +) Các cạnh bên của hình lăng trụ song song và bằng nhau.

    +) Các mặt bên của hình lăng trụ là các hình bình hành.

    +) Hai đáy của hình lăng trụ là hai đa giác bằng nhau và nằm trên hai mặt phẳng song song.

    +) Tên gọi của lăng trụ được gọi theo tên đa giác đáy: lăng trụ tam giác, lăng trụ tứ giác, lăng trụ ngũ giác,…

    b) Hình hộp

    Định nghĩa: Hình lăng trụ có đáy là hình bình hành được gọi là hình hộp.

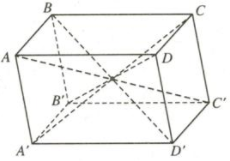
    Tính chất:

    +) Hình hộp có \(6\) mặt là những hình bình hành.

    +) Hai mặt song song với nhau là hai mặt đối diện của hình hộp.

    +) Hình hộp có \(8\) đỉnh, hai đỉnh không cùng nằm trên mặt nào của hình hộp được gọi là hai đỉnh đối diện.

    +) Đoạn thẳng nối hai đỉnh đối diện được gọi là đường chéo của hình hộp.

    +) Bốn đường chéo của hình hộp cắt nhau tại trung điểm mỗi đường, gọi là tâm hình hộp.

    2. Hình chóp cụt

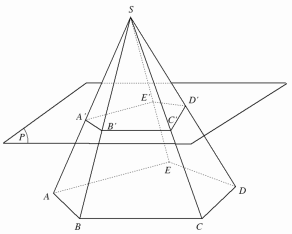
    Hình trên cho ta một hình chóp cụt được tạo thành từ việc cắt hình chóp \(S.ABCDE\) bởi mặt phẳng \(\left( P \right)\) song song với đáy.

    Tính chất:

    Hình chóp cụt có:

    a) Hai đáy là hai đa giác có cạnh tương ứng song song và tỉ số các cạnh tương ứng bằng nhau.

    b) Các mặt bên là những hình thang.

    c) Các đường thẳng chứa các cạnh bên đồng quy tại một điểm.

    3. Phương pháp chứng minh hai mặt phẳng song song

    Phương pháp 1:

    - Bước 1: Chứng minh mặt phẳng \(\left( \alpha  \right)\) chứa hai đường thẳng \(a,b\) cắt nhau lần lượt song song với hai đường thẳng \(a',b'\) cắt nhau trong mặt phẳng \(\left( \beta  \right)\).

    - Bước 2: Kết luận \(\left( \alpha  \right)//\left( \beta  \right)\).

    Phương pháp 2:

    - Bước 1: Tìm hai đường thẳng \(a,b\) cắt nhau trong mặt phẳng \(\left( \alpha  \right)\).

    - Bước 2: Lần lượt chứng minh $a//\left( \beta  \right)$ và $b//\left( \beta  \right)$ 

    - Bước 3: Kết luận \(\left( \alpha  \right)//\left( \beta  \right)\).

    Xem toàn bộ nội dung Toán 11:

    (394) 1313 29/07/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 11 Toán 11